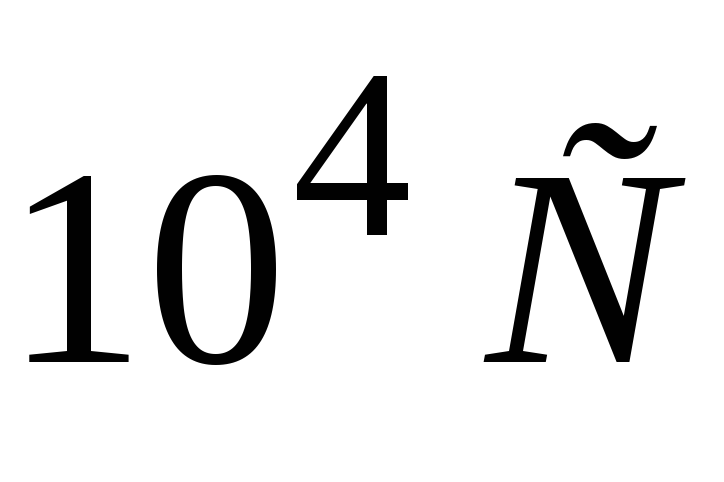Числа Белла
Число Белла равно количеству разбиений множества из элементов на произвольное количество непустых подмножеств, которые не пересекаются. Очевидно, что, так как существует только одно разбиение пустого множества. Например,, так как существует 5 возможных разбиений множестваиз трех элементов:
Заметим, что элементов можно разбить намножеств. При этом количество разбиений– элементного множества наподмножеств равно числу Стирлинга 2 рода. Откуда получаем формулу:
0 | 1 | 2 | 3 | 4 | 5 | 7 | 8 | 9 | 10 | ||
1 | 1 | 2 | 5 | 15 | 52 | 203 | 877 | 4140 | 21147 | 115975 |
Рассмотрим следующие
конструкции, в которых точки обозначают
одноэлементные множества, а сегменты
объединяют элементы, принадлежащие
одному множеству.
Из
элементов можно построитьразных таких конструкций.
Теорема. Числа Белла удовлетворяют следующему рекуррентному соотношению:
Доказательство. Рассмотрим разбиение элемента в зависимости от величины блока, в котором находится– ый элемнент. Пусть размер этого блока равен. Тогда существуетспособов выбрать в него кроме– ого ешеэлемент. Остальныеэлементов можно разбитьспособами.Таким образом:
Пример.Например, . Числа Белла удовлетворяют следующему свойству:
Для значений получим следующие значения детерминанта:
1, 1, 2, 12, 288, 34560, 24883200, 125411328000, 5056584744960000, 1834933472251084800000, 6658606584104736522240000000, …
При разложении функции в ряд Маклорена коэффициенты ряда образуют числа Белла:
Числа
могут быть построены при помощитреугольника Белла.
Композиции
При решении задач про распределениеодинаковых предметов междунепустыми урнами можно говорить о разложении числав сумму натуральных слагаемых:
, где(5.18)
Два таких разложения числа считаются разными, если они отличаются хотя бы одним слагаемым. В таком случае говорят о композиции числа. В ином случае,композиция числа –это его разложение в виде (5.18), где учитываются как величины слагаемых (частей) , так и порядок их расположения в сумме.
Пример. Выписать все композиции числа 3.
3=3, 3=2+1, 3=1+2, 3=1+1+1.
Композиции с ограничениями на количество слагаемых
Число композиций
числаизслагаемых равно числу распределенийодинаковых предметов поразным урнам при условии отсутствия
пустых урн.
Число предметов, которые
попали в урну с номером,
дает слагаемое . Отсюда выплывает, что.
Число всех композиций числа
(5.19)
Комбинаторика разбиений
При анализе стратегий различных игр требуется подсчитывать количество комбинаций при раскладе определенных предметов. Наиболее распространенная карточная игра – преферанс. В классическом варианте этой игры карты раскладываются на 3 кучки (по числу играющих) и 2 карты кладутся в “прикуп“. Играют 32 картами, т. е. каждый игрок получает по 10 карт.
Определим количество вариантов расклада при игре в преферанс:
Для обоснования полученной формулы
расставим все карты подряд и переставим
их 32! способами. При каждой перестановке
будем выделять первые 10 карт первому
игроку, вторую десятку – второму, третью
– третьему, а последние 2 карты будем
откладывать в “прикуп”. После этого
заметим, что перестановка 10 карт в руках
каждого игрока не меняет варианта
расклада, как и положения 2 карт в прикупе.
В общем случае, если раскладываются разных предметов поящикам так, чтобы в 1-й ящик (кучку, игроку в руки) попалопредметов, во второй предмета, в-й –предметов, при этом, то число вариантов расклада
(5.20)
Число Белла
множества B A , содержащего элемент n, существует в точности
S(n-b,k-1) разбиений множества А на k блоков, содержащих B в качестве блока. Действительно, каждое такое разбиение однозначно соответствует разбиению множества А\В на k-1 блоков. b- элементное множество B A , содержащее элемент n, можно выбрать С(n-1,b-1) способами. Следовательно
S(n, k)
n−(k −1)
= ∑
b=1
n−(k −1)
= ∑ Cb−−1S(n −b, k −1) =
n 1
b=1
n−1
Cn−−b S(n −b, k −1) = ∑Ci − S(i, k −1).
n 1 n 1 i=k −1
Определение. Число Белла Bn есть число всех разбиений n- элементного множества Bn = Π (A) , где A = n.
Другими словами
n
Bn = ∑
k =0
Теорема
S(n, k).
n
3.3. B + = ∑Ci B .
n 1 n i i=0
Доказательство.
Множество всех разбиений множества A={1,…,n+1} можно разбить на различные классы в зависимости от блока В, содержа-
щего элемент n+1 | (или в зависимости от множества А\В). Для каж- | ||||||||
дого множества | A \ B {1,…, n} существует в точности | ||||||||
|
| Π ( A \ B) |
| = B |
| A−B |
|
| разбиений множества А, содержащих В в каче- |
|
| ||||||||
|
|
|
|
| |||||
|
|
|
|
|
|
|
|
|
|
стве блока.
Группируя классы в зависимости от мощности множества А\В, получаем требуемую формулу.
B(0)=1
B(1)=1
B(2)=2
B(3)=5
B(4)=15
B(5)=52
B(6)=203
Таблица 3.2. Числа Белла.
12
Числа Стирлинга первого рода
Введем следующее обозначение многочлена
[x]k | = x(x −1)…(x −k +1) |
| |
Для частных случаев: |
| ||
[x]0 | =1, | . | |
[x]1 =1, | |||
| |||
[x]2 | = x(x −1), |
| |
[x]3 | = x(x −1)(x −2). |
| |
Определение. Числа Стирлинга первого рода s(n,k) есть коэффициенты при последовательных степенях переменной x в много-
члене [x]k :
n |
|
[x]n = ∑s(n, k)xk . |
|
k =0 |
|
Очевидно, что s(n,k)=0 для k>n. |
|
Теорема 3.4. |
|
s(n, k) = s(n −1, k −1) −(n −1)s(n −1, k) , для 0 < k < n, | (3.4) |
s(n, n) =1 , для n ≥ 0, | (3.5) |
s(n,0) = 0 , для n >0. | (3.6) |
Доказательство.
Формулы (3.5) и (3.6) очевидны. Формулу (3.4) получим, сравнивая коэффициенты при xk в обеих частях равенства
[x]n =[x]n−1 (x −n +1).
Имеем
| n |
| n−1 |
|
|
|
|
|
| |
∑s(n, k)xk = (x −n =1)∑s(n −1, k)xk = |
|
| |||||||
k =0 |
| k =0 |
|
|
|
|
|
| |
n−1 |
|
| n−1 |
|
|
| |||
= ∑s(n −1, k)xk +1 −(n −1)∑s(n, k)xk = |
|
| |||||||
k =0 |
|
| k =0 |
|
|
| |||
n−1 |
|
|
|
|
|
|
| ||
∑(s(n −1, k −1) −(n −1)s(n −1, k))xk + |
|
| |||||||
k =1 |
|
|
|
|
|
|
|
| |
+ s(n −1, n −1)xn −(n −1)s(n −1,0). |
|
|
| ||||||
| k | 0 | 1 |
| 2 |
| 3 | 4 | 5 |
|
|
|
|
|
|
|
|
|
|
13
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 | 1 | 0 | 0 | 0 | 0 | 0 |
1 | 0 | 1 | 0 | 0 | 0 | 0 |
2 | 0 | -1 | 1 | 0 | 0 | 0 |
3 | 0 | 2 | -3 | 1 | 0 | 0 |
4 | 0 | -6 | 11 | -6 | 1 | 0 |
5 | 0 | 24 | 50 | 35 | -10 | 1 |
Таблица 3.
3. Числа Стирлинга первого рода.
Лекция 4. Формулы включений и исключений.
Формулы включений и исключений
Лемма 4.1. Пусть дано N элементов и n свойств p1,…,pn. Пусть Ni1 …ir — число элементов, обладающих, по крайней мере, свойст-
вами pi1 ,… pir ,r =1,n . Тогда число элементов N0 , не обладающих ни одним из указанных свойств определяется формулой
n |
| ∑Ni1 …is |
|
N0 = N −∑Ni + ∑Ni1i2 +… +(−1)s | +… | ||
i=1 | i1 <i2 | i1 <i2 <…<is | (4.1) |
+(−1)n N12…n
Доказательство. Рассмотрим правую часть (4.1). Элемент, не обладающий свойствами p1,…,pn, учитывается только в слагаемом N. Любой элемент A, обладающий ровно r свойствами j1,…,jr учитывается в выражении
∑Ni1…is , s ≤ r, Crs раз.
i1<i2 <…<is
Следовательно, вклад A в правую часть (4.1) равен:
1−Cr1 +Cr2 +… +(−1)s Crs +… +(−1)r Crr = (1−1)r = 0r = 0 .
Пример 4.1. (пояснение к предыдущей формуле)
Рассмотрим множество шаров, которые могут быть окрашены в 4 цвета:
желтый – свойство 1; красный – свойство 2; синий – свойство 3; зеленый – свойство 4.
Пусть некоторый шар окрашен одновременно в желтый, красный и зеленый цвета. Тогда для него N0 = 0. Теперь рассмотрим,
14
какой вклад он дает в правую часть равенства (4.1).
В первом слагаемом он учитывается 1 раз. Во втором слагаемом он учитывается C31 =3 раза (т.к. N1 = 1, N2 = 1, N4 = 1). В
третьем слагаемом он учитывается C32 =3 раза (т.к. N12 = 1, N14 = 1, N24 = 1). В четвертом слагаемом он учитывается C33 =1 раз (т.к.
N124=1). В пятом (последнем для рассматриваемого примера) сла-
гаемом он учитывается 0 раз (т.к. N1234 = 0).
Таким образом, вклад рассматриваемого шара в правую часть равенства (4.
1) равен 1 – 3 + 3 – 1 + 0 = 0.
Замечание. Формула (4.1) называется формулой включений и исключений.
Пример 4.2. (задача о беспорядках).
Определить количество перестановок a1,…,an, чисел 1,…,n та-
ких, что ai ≠ i,i =1,n .
Решение. Число всех перестановок N=n!
Свойство si : ai = i,i = 1, n .
Ni1 ,…,ir — число перестановок, оставляющих на месте по крайней мере числа i1,…,ir , следовательно, Ni1 ,…,ir = (n − r)!
В ∑Ni1 ,…,ir имеется Cnr слагаемых – количество способов
i1 <…<ir
выбора чисел i1,…,ir из 1,…,n. Итак, на основании (4.1):
N0 = n!−Cn1 (n −1)!+Cn2 (n − 2)!+… + (−1)r Cnr (n − r)!+…
+(−1)n Cnn 0! = n!(1−1+ | 1 | +… + (−1)r | 1 |
| +… + (−1)n | 1 | ) = | ||
| r! |
| |||||||
| 2! |
| n! | ||||||
n | 1 |
|
|
|
|
|
|
|
|
= n!∑(−1)r |
|
|
|
|
|
|
|
| |
r! |
|
|
|
|
| ||||
r =2 |
|
|
|
|
| ||||
Лемма 4. |
|
|
|
|
| ||||
n |
|
|
|
|
|
|
|
|
|
∑(−1)k −r CnkCkr = 0, n, r N, n ≥ r |
|
|
| (4.2) | |||||
k =r |
|
|
|
|
|
|
|
|
|
Доказательство. Рассмотрим тождество |
|
| |||||||
n |
|
|
|
|
|
|
|
|
|
(1 + x)n = ∑Cnk xk |
|
|
| (4. | |||||
2 (вспомогательная)
3)k =0
15
Дифференцируя (4.3) r раз по x, получим
|
|
|
|
| n |
| |
n(n −1)…(n − r +1)(1 + x)n−r = ∑Cnk k(k −1)…(k − r +1)xk −r . | |||||||
|
|
|
|
| k =r |
| |
Последнее равенство преобразуется к виду | |||||||
| n! |
| n |
| k! |
|
|
| (1+ x)n−r = ∑Cnk |
| xk −r . | ||||
| (n −r)! |
| (k −r)! | ||||
| k =r |
|
| ||||
Разделив обе части на r! приходим к соотношению | |||||||
|
|
| n |
|
|
|
|
Cnr (1 + x)n−r = ∑Cnk Ckr xk | −r , |
| |||||
|
|
| k =r |
|
|
|
|
которое при x = −1 дает |
| ||||||
| n |
|
|
|
|
| |
∑(−1)k −r Cnk Ckr = 0 . |
|
|
|
| |||
| k =r |
|
|
|
|
| |
Лемма 4.3. Пусть дано N элементов и n свойств s1,…,sn. Пусть Ni1…ir — число элементов, обладающих по крайней мере свойствами
i1,…,ir, r =1, n . Тогда число элементов N(r), обладающих ровно r свойствами определяются формулой
N (r) = ∑ Ni1 …ir + | + (−1)s−r Csr | ∑ | Ni1 …is + |
1≤i1 <…<is ≤n | 1≤i1 | <…<is ≤n | (4.4) |
| n |
| |
+ (−1)n−r Cnr N12…n = ∑(−1)n−s Csr | ∑ | Ni1 …is . | |
| s=r | 1≤i1 <. | |
..<is ≤nДоказательство. В левой части (4.4) элемент с ровно r свойствами учитываются один раз. В правой части (4.4) элемент с ровно r свойствами учитываются один раз в первом слагаемом и не учитываются далее. Элемент с ровно t свойствами, t>r, учитывается
(−1)s−r CsrCts раз в слагаемом (−1)s−r Csr ∑ Ni1 …is .
1≤i1 <…<is ≤n
Поэтому вклад от элементов с ровно t свойствами, t>r, состав-
t
ляет∑(−1)s−r Csr Cts . В силу леммы 4.2 эта сумма равна нулю.
s=r
Пример 4.3 (задача о встречах). Определить количество перестановок a1,…,an чисел 1,…,n , для которых ai=i ровно в r местах.
16
k A_i=S$ и для каждого $i\not=j$, $A_i\cap A_j=\emptyset$. $\квадрат$Пример 1.4.2. Разбиения множества $\{a,b,c\}$ равны $\{\{a\},\{b\},\{c\}\}$, $\{\{a,b\},\{c\}\}$, $\{\{a ,с\},\{б\}\}$, $\{\{b,c\},\{a\}\}$ и $\{\{a,b,c\}\}$. $\квадрат$
Разделы возникают в ряде областей математики. Например, если
$\equiv$ — отношение эквивалентности на множестве $S$, эквивалентность
классы $\equiv$ образуют раздел $S$.
n {n\выберите k} B_k,
$$
написано наоборот.
$\qed$
93 {3\выберите k}B_k = 1\cdot 1 + 3\cdot 1 + 3\cdot 2 +
1\cточка 5 = 15\кр
}
$$
$\квадрат$
Числа Белла растут экспоненциально быстро; первые несколько 1, 1, 2, 5, 15, 52, 203, 877, 4140, 21147, 115975, 678570, 4213597, 27644437.
Числа Белла появляются во многих других задачах; вот
интересный пример. Обычная потребность в некоторых компьютерных программах состоит в том, чтобы
генерировать случайную перестановку $1,2,3,\ldots,n$, которую мы можем подумать
как перетасовка чисел, визуализированная как пронумерованные карты в
палуба. Вот привлекательный метод, который легко запрограммировать: Начните с
числа по порядку, затем на каждом шаге убирайте одно число случайным образом
(это легко сделать в большинстве языков программирования) и поместите его на передний план
из списка номеров. (Рассматриваемый как перетасовка колоды карт, это
соответствует удалению карты и помещению ее на верх колоды.)
Сколько раз мы должны это сделать? Волшебного числа нет, но оно
конечно, не должен быть маленьким по сравнению с размером $n$.
m$.) Так как существует
всего $n!$ различных перестановок $1,2,\ldots,n$, это означает
что многие перетасовки дают один и тот же окончательный порядок.
Вот наш вопрос: сколько перетасовок приводит к исходному порядку?
Пример 1.4.6. Эти перетасовки возвращаются к исходному порядку: $(1,1,1,1,1)$, $(5,4,3,2,1)$, $(4,1,3,2,1)$. $\квадрат$
Теорема 1.4.7 Количество перетасовок $[n]$, в результате которых исходный порядок сортировки $B_n$.
Доказательство. Поскольку мы знаем, что $B_n$ подсчитывает количество разделов
$\{1,2,3,\ldots,n\}$, мы можем доказать теорему, установив 1–1
соответствие между тасовками, которые оставляют колоду отсортированной, и
перегородки. Учитывая перетасовку $(m_1,m_2,\ldots,m_n)$, мы помещаем в
single устанавливает все $i$ так, что $m_i$ имеет единственное значение. Например,
используя перетасовку $(4,1,3,2,1)$, так как $m_2=m_5$, один набор
$\{2,5\}$. Все остальные значения различны, поэтому другие наборы в
раздела: $\{1\}$, $\{3\}$ и $\{4\}$.
Обратите внимание, что каждое перемешивание, независимо от окончательного порядка, производит разделить этим методом. Нас интересуют только те перетасовки, которые оставьте колоду в порядке. Теперь нам нужно показать, что каждый раздел результат ровно одной такой перетасовки.
Предположим, у нас есть раздел с $k$ частями. Если при тасовке колода остается отсортированной, последняя запись, $m_n$, должна быть 1. Если часть, содержащая $n$, равна $A_1$, то она должна быть такой $m_i=1$ тогда и только тогда, когда $i\in A_1$. Если $k=1$, то единственная часть содержит все $\{1,2,\ldots,n\}$, и перетасовка должна быть $(1,1,1,\ldots,1)$.
Если $k>1$, последний ход, отличный от 1, должен быть 2, так как 2 должно закончиться
сразу после 1. Таким образом, если $j_2$ — наибольший индекс такой, что
$j_2\notin A_1$, пусть $A_2$ — часть, содержащая $j_2$, и она должна быть
что $m_i=2$ тогда и только тогда, когда $i\in A_2$. Продолжаем так: Один раз
мы выяснили, какие из $m_i$ должны иметь значения $1,2,\ldots,p$,
пусть $j_{p+1}$ будет наибольшим индексом таким, что
$j_{p+1}\notin A_1\cup\cdots\cup A_p$, пусть $A_{p+1}$ — часть
содержащий $j_{p+1}$, а затем $m_i=p+1$ тогда и только тогда, когда $i\in
А_{р+1}$.
n$, и это оказывается немного больше, чем
$1/n!$. Таким образом, это не подходящий метод для генерации случайных
перестановки.
Приведенное выше рекуррентное соотношение представляет собой несколько громоздкий способ вычисления Звонковые числа. Другой способ их вычисления — с другим рецидив, выраженный в Треугольник колокола, конструкция которого аналогична треугольник Паскаля: $$\матрица{ А_{1,1}\кр А_{2,1}&А_{2,2}\кр А_{3,1}&А_{3,2}&А_{3,3}\кр A_{4,1}&A_{4,2}&A_{4,3}&A_{4,4}\cr} \qquad\matrix{ 1\кр 1&2\кр 2&3&5\кр 5&7&10&15\кр} $$ Правило построения этого треугольника: $A_{1,1}=1$; первый запись в каждой строке является последней записью в предыдущей строке; другие записи $A_{n,k}=A_{n,k-1}+A_{n-1,k-1}$; строка $n$ содержит $n$ записей. Оба первый столбец и диагональ состоят из чисел Белла, с $A_{n,1}=B_{n-1}$ и $A_{n,n}=B_n$.
$A_{n,k}$ можно интерпретировать как количество разделов
$\{1,2,\ldots,n+1\}$ в
который $\{k+1\}$ является набором синглетонов с самой большой записью в разделе.
Например, $A_{3,2}=3$; разбиения $3+1=4$, в которых $2+1=3$
это наибольшее число, появляющееся в одноэлементном наборе,
$\{\{1\},\{2,4\},\{3\}\}$, $\{\{2\},\{1,4\},\{3\}\} $ и $\{\{1,2,4\},\{3\}\}$.
Чтобы увидеть, что это действительно работает так, как рекламируется, нам нужно подтвердить несколько вещи. Во-первых, рассмотрим $A_{n,n}$, число разделов $\{1,2,\ldots,n+1\}$, в котором $\{n+1\}$ — одноэлементное множество с самая большая запись в разделе. Так как $n+1$ — наибольший элемент множества, все разбиения, содержащие один элемент $\{n+1\}$, удовлетворяют требование, и поэтому $B_n$ разделов $\{1,2,\ldots,n\}$ вместе с $\{n+1\}$ представляют собой в точности интересующие нас разбиения, которые есть, $A_{n,n}=B_n$.
Далее проверяем, что при желаемой интерпретации действительно
верно, что $A_{n,k}=A_{n,k-1}+A_{n-1,k-1}$ для $k>1$. Рассмотрим
раздел считается $A_{n,k-1}$. Это содержит синглтон $\{k\}$,
и элемент $k+1$ не является одноэлементным. Если мы поменяем местами $k$ и
$k+1$, мы получаем одноэлементный $\{k+1\}$, и ни один больший элемент не находится в
синглтон.
Это дает нам разделы, в которых $\{k+1\}$ является синглтоном.
а $\{k\}$ — нет. Теперь рассмотрим раздел $\{1,2,\ldots,n\}$
подсчитывается $A_{n-1,k-1}$. Замените все числа $j>k$ на $j+1$ и добавьте
синглетон $\{k+1\}$. Это создает раздел, в котором оба
Появляются $\{k+1\}$ и $\{k\}$. Собственно, мы описали, как
производить каждый раздел, подсчитываемый $A_{n,k}$, ровно один раз, и поэтому
$A_{n,k}=A_{n,k-1}+A_{n-1,k-1}$.
Наконец, нам нужно убедиться, что $A_{n,1}=B_{n-1}$; мы устанавливаем
биекция между двумя множествами. Предположим, что раздел в $A_{n,1}$ имеет
вид $\{\{1\},\{2\},X_1,X_2,\ldots,X_k\}$, где нет $X_i$
является синглтоном. Тогда коллекция
$\{X_1,X_2,\ldots,X_k\}$ — разбиение множества $n-1$ элементов
$\{3,4,\ldots, n+1\}$. Теперь мы вычитаем 2 из каждого элемента, чтобы получить
разбиение $[n-1]$, не имеющее одноэлементных множеств. Любой другой раздел в
$A_{n,1}$ имеет вид $\{\{2\},X_1,X_2,\ldots,X_k\}$, где нет $X_i$
является синглтоном. Одно из множеств $X_i$ содержит $n+1$, скажем
$Х_1$.
Удалите $n+1$ и разделите остаток $X_1$ на синглтоны.
устанавливает $\{x_1\}, \{x_2\},\ldots, \{x_m\}$. Сейчас
$\{\{x_1\}, \{x_2\},\ldots, \{x_m\},X_2,X_3,\ldots,X_k\}$ — это
разбиение множества $n-1$ элементов $\{1,3,\ldots,n\}$. Вычитание одного
из всех элементов, кроме 1, получается разбиение $[n-1]$ с at
хотя бы один одноэлементный набор. Если $p\in A_{n,1}$, укажите разбиение
$[n-1]$, полученный таким образом с помощью $f(p)$.
92$ делит $n$; Другими словами, числа без квадратов являются произведениями
различных простых множителей, то есть $n=p_1p_2\cdots p_k$, где каждый
$p_i$ — простое число, и никакие два простых множителя не равны.
Найдите количество факторизаций $n$. Например, $30=2\cdot
3\cdot 5$, а факторизация 30 равна 30, $6\cdot 5$, $10\cdot
3$, $2\cdot 15$ и $2\cdot 3\cdot 5$. Обратите внимание, что мы считаем только 30 как
факторизация, хотя в некотором смысле и тривиальная факторизация.
Пример 1.4.3 Схема рифмовки строфы стихотворения указывает, какие строки
рифма.
Обычно это выражается в форме ABAB, что означает первый
и третьи строки четырехстрочной строфы рифмуются, как и вторая и
четвертая, или ABCB, означающая, что рифмуются только вторая и четвертая строки, и так далее. А
лимерик — пятистрочное стихотворение со схемой рифмовки AABBA. Сколько
возможны разные схемы рифмовки для строфы из $n$ строк? Избегать
повторяющиеся шаблоны, мы допускаем новую букву в шаблон только тогда, когда
все предыдущие буквы использовались слева от новой. Для
Например, ACBA не допускается, так как когда C помещается в позицию 2, B
слева не использовался. Это та же схема рифмовки, что и ABCA,
что разрешено.
9nS(n,k),
$$
где $S(n,k)$ — количество разбиений $\{1,2,\ldots,n\}$ на
ровно $k$ частей, $1\le k\le n$. $S(n,k)$ — это Числа Стирлинга второго рода .
Найдите рекуррентное соотношение для
$S(n,k)$. Ваше повторение должно позволять довольно простой треугольник
построение, содержащее значения $S(n,k)$, а затем числа Белла
можно вычислить, суммируя строки этого треугольника.
{n+1} A(n,k).
$$
Найдите повторение для $A(n,k)$ и покажите, что $A_n=B_n$.
Больше дискретной математики через теорию графов
\( \def\negchoose#1#2{\genfrac{[}{]}{0pt}{}{#1}{#2}_{-1}}
\newcommand{\mchoose}[2]{\left(\!\binom{#1}{#2}\!\right)}
\newcommand{\cycle}[1]{\arraycolsep 5 pt
\left(\begin{массив}#1\конец{массив}\right)}
\newcommand{\importantarrow}{\Rightarrow}
\newcommand{\qchoose}[2]{\left[{#1\top#2}\right]_q}
\ новая команда {\ bp} {
\begin{enumerate}{\setcounter{enumi}{\value{номер_проблемы}}}}
\newcommand{\ep}{\setcounter{номер_проблемы}{\значение{enumi}}
\конец{перечислить}}
\ новая команда {\ игнорировать} [1] {}
\renewcommand{\bottomfraction}{.8}
\renewcommand{\topfraction}{.8}
\newcommand{\apple}{\text{🍎}}
\newcommand{\ap}{\яблоко}
\newcommand{\банан}{\текст{🍌}}
\ новая команда {\ ba} {\ банан}
\newcommand{\груша}{\текст{🍐}}
\newcommand{\pe}{\груша}
\DeclareMathOperator{\Fix}{Fix}
\DeclareMathOperator{\Orb}{Orb}
\newcommand{\F}{\mathcal{F}}
\новая команда{\предупреждение}{\fbox}
\def\d{\displaystyle}
\def\курс{Математика 228}
\ новая команда {\ f} [1] {\ mathfrak # 1}
\ новая команда {\ s} [1] {\ mathscr # 1}
\def\N{\mathbb N}
\def\B{\mathbf{B}}
\def\circleA{(-.
{-1}}
\def\nrml{\triangleleft}
\ деф \ ст {:}
\ деф \ ~ {\ широкая тильда}
\def\rem{\mathcal R}
\def\sigalg{$\sigma$-алгебра }
\def\Гал{\mbox{Гал}}
\def\iff{\leftrightarrow}
\def\If{\Leftrightarrow}
\ деф \ земля {\ клин}
\def\И{\bigwedge}
\защита\вход{\вход}
\def\AAnd{\d\bigwedge\mkern-18mu\bigwedge}
\def\Ви{\bigvee}
\def\VVee{\d\Vee\mkern-18mu\Vee}
\ деф \ имп {\ стрелка вправо}
\def\Imp{\Rightarrow}
\def\Fi{\Leftarrow}
\def\var{\mbox{var}}
\def\Th{\mbox{Th}}
\защита\вход{\вход}
\def\sat{\mbox{Sat}}
\def\con{\mbox{Con}}
\def\iffmodels{\bmodels\models}
\def\dbland{\bigwedge \!\!\bigwedge}
\def\дом{\mbox{дом}}
\def\rng{\mbox{диапазон}}
\def\isom{\cong}
\DeclareMathOperator{\wgt}{wgt}
\newcommand{\vtx}[2]{узел[заливка,круг,внутренний интервал=0pt, минимальный размер=4pt,метка=#1:#2]{}}
\ новая команда {\ va} [1] {\ vtx {выше} {# 1}}
\ новая команда {\ vb} [1] {\ vtx {ниже} {# 1}}
\ новая команда {\ vr} [1] {\ vtx {право} {# 1}}
\ новая команда {\ vl} [1] {\ vtx {слева} {# 1}}
\renewcommand{\v}{\vtx{выше}{}}
\def\circleA{(-.
5,0) круг (1)}
\def\circleAlabel{(-1.5,.6) узел[выше]{$A$}}
\def\circleB{(.5,0) круг (1)}
\def\circleBlabel{(1.5,.6) узел[выше]{$B$}}
\def\circleC{(0,-1) круг (1)}
\def\circleClabel{(.5,-2) узел[справа]{$C$}}
\def\twosetbox{(-2,-1.4) прямоугольник (2,1.4)}
\def\threesetbox{(-2.5,-2.4) прямоугольник (2.5,1.4)}
\def\ansfilename{практика-ответы}
\def\shadowprops{{fill=black!50,shadow xshift=0.5ex,shadow yshift=0.5ex,path fading={круг с размытым краем 10 процентов}}}
\ новая команда {\ hexbox} [3] {
\def\x{-cos{30}*\r*#1+cos{30}*#2*\r*2}
\def\y{-\r*#1-sin{30}*\r*#1}
\рисовать (\х,\у) +(90:\r) — +(30:\r) — +(-30:\r) — +(-90:\r) — +(-150:\r) — +(150: \r) — цикл;
\draw (\x,\y) узел{#3};
}
\newcommand{\card}[1]{\left| #1 \справа|}
\newcommand{\twoline}[2]{\begin{pmatrix}#1 \\ #2 \end{pmatrix}}
\новая команда{\lt}{<}
\новая команда{\gt}{>}
\newcommand{\amp}{&}
\)
Число Белла, \(B_{k}\text{,}\), обозначает количество способов, которыми множество \(k\) объектов может быть разделено на непустые подмножества.
kS(k,n)\text{.}\)
Последовательность номеров Белла начинается с
\begin{уравнение*} 1, 1, 2, 5, 15, 52, 203, 877, 4040, 21147, 115975, \ldots \end{уравнение*}
Обратите внимание, что первые четыре цифры выглядят как каталонские. На самом деле, одна из многих вещей, которые подсчитывают каталонские числа, — это 90 103 непересекающихся 90 104 множества разделов. Как только вы поверите в это, вы увидите, что \(C_n \le B_n\) для всех \(n\text{.}\)
Числа Белла могут быть получены путем построения так называемого треугольника Белла. Чтобы построить этот треугольник, начните с 1 вверху и 1 под ним. Сложите эти два числа вместе и поставьте сумму 2 справа от 1 во втором столбце. Эта цифра 2 также является первой записью третьей строки. Вторая запись в третьей строке находится путем прибавления 2 к числу 1 над ней. Эта сумма равна 3 и идет справа от 2. 3 теперь ниже 2. Сложение этих двух чисел дает последнее число 5 в третьей строке. Поскольку над цифрой 5 нет числа, третья строка завершена.
5 теперь становится первым числом в четвертой строке, и процесс продолжается.
| 1 | ||||||
| 1 | 2 | |||||
| 2 | 3 | 5 | ||||
| 5 | 7 | 10 | 15 | |||
| 15 | 20 | 27 | 37 | 52 | ||
| 52 | 67 | 87 | 114 | 151 | 203 | |
| 203 | 255 | 322 | 409 | 523 | 674 | 877 |
Подводя итог, можно сказать, что построение треугольника следует двум основным правилам:
Последнее число каждой строки является первым числом следующей строки.
Все остальные числа находятся путем прибавления числа слева от пропущенного числа к числу непосредственно над этим же числом.
Когда треугольник расширяется, как указано выше, номера колоколов находятся как в первом столбце, так и по внешней диагонали.
Активность297
Почему эта конструкция треугольника дает вам числа Белла? Объясните с точки зрения набора разделов.
Как и треугольник Паскаля, треугольник Белла обладает несколькими интересными свойствами.
Активность298
Если сумма ряда прибавляется к номеру Белла в конце этой строки, получается следующий номер Белла. Например, сумма четвертой строки плюс число Белла в конце строки: \(15 + 20 + 27 + 37 + 52 + 52\) равно 203, следующему числу Белла. Почему это происходит?
Активность299
Еще одна закономерность, которую вы можете заметить: числа второй диагонали \(1, 3, 10, 37, 151, 674, \ldots\) являются суммами горизонтальных рядов. Докажи это!
Небольшой поворот треугольника создает разностный треугольник, аналогичный треугольнику Паскаля. Записи, которые формируются рекурсивно путем сложения в треугольнике Паскаля, теперь являются разностью двух чисел над ними в треугольнике Белла.
| 1 | 2 | 5 | 15 | 52 | 203 | 877 | \(\ldots\) | ||||||
| 1 | 3 | 10 | 37 | 151 | 674 | \(\ldots\) | |||||||
| 2 | 7 | 27 | 114 | 523 | \(\ldots\) | ||||||||
| 5 | 20 | 87 | 409 | \(\ldots\) | |||||||||
| 15 | 67 | 322 | \(\ldots\) | ||||||||||
| 52 | 255 | \(\ldots\) | |||||||||||
| 203 | \(\ldots\) |
Активность300
Объясните, почему различия работают именно так, как в повернутом треугольнике.
{\text{th}}\) может быть рекурсивно представлено как \(B_{n + 1} = \binom{n}{0} B_{ 0} + \binom{n}{1} B_{1} + \binom{n}{2}B_{2} + \ldots + \binom{n}{n} B_{n}\text{.}\ ) Коэффициенты этого уравнения являются элементами \(n\)-й строки треугольника Паскаля.
Активность301
Доказать повторяемость
\begin{уравнение*} B_{k + 1} = \binom{k}{0} B_{0} + \binom{k}{1} B_{1} + \binom{k}{2}B_{2} + \ldots + \ бином {к} {к} В_ {к} \end{equation*}
Числа Белла связаны с числами Стирлинга и могут быть определены как сумма чисел Стирлинга второго рода. То есть \(B_{k} = S(k,1) + S(k,2) + \cdots + S(k,k)\text{,}\), где \(S(k,n)\ ) представляет количество способов группировки \(k\) элементов в \(n\) подмножеств. Итак, \(B_{3} = S(3,1) + S(3,2) + S(3,3) = 1 + 3 + 1 = 5\text{.}\) Поскольку числа Белла учитывают разбиения набора элементов, они используются в теории простых чисел для перечисления количества способов разложения числа на множители с различными простыми множителями.
Например, число 42 имеет три различных простых делителя: 2, 3 и 7. Поскольку \(B_{3} = 5\) , мы знаем, что существует пять способов разложения 42 на множители. Это \(2 \times 3 \times 7 \text{,}\) \(2 \times 21\text{,}\) \(3 \times 14\text{,}\) \(6 \times 7\text{,}\) и \(42 \text{.}\) Таким образом, число \(210\text{,}\), имеющее 4 различных делителя, 2, 3, 5 и 7, можно разложить на множители \(B_{4} = 15\) способов .
Числа Белла можно использовать для моделирования многих реальных ситуаций. Например, количество различных способов, которыми два человека могут спать на немаркированных односпальных кроватях, равно \(B_{2} = 2\) способов: они могут спать в одной кровати или в разных кроватях. Количество способов сервировки обеда, состоящего из трех блюд, таких как салат, хлеб и рыба, равно \(B_{3} = 5\) способов: каждое можно подать на отдельной тарелке, салат и хлеб — на одна тарелка и рыба на другой, салат и рыба на одной тарелке и хлеб на другой, или все три блюда могут быть на одной тарелке.
Этот пример служит моделью для пяти способов, которыми три человека могут занимать три немаркированные кровати, пяти способов, которыми трое заключенных могут быть скованы вместе наручниками, пяти способов, которыми три нации могут образовывать союзы, или любой ситуации разделения трех отдельных элементов на непустые. подмножества.
Одним из интересных применений чисел Белла является подсчет количества схем рифмовки, возможных для строфы в стихах. Есть \(B_{2} = 2\) возможностей для двухстрочной строфы: строки могут либо рифмоваться, либо не рифмоваться. Возможные схемы рифмовки трехстрочной строфы можно описать как aaa, aab, aba, abb и abc: таким образом, существует 5 или \(B_{3}\) возможных схем рифмовки. Японцы использовали диаграммы, изображающие возможные схемы рифмовки пятистрочной строфы \(B_{5} = 52\), еще в 1000 г. н.э. в 9 в.0103 Сказка о Гэндзи леди Шикибу Мурасаки.
Завершаем интересным занятием.
Активность302
Набор \(\{u_{0}, u_{1}, u_{2}, \ldots \}\), где \(u_{0} = 1\text{,}\) \(u_{1} = x\text{,}\) \(u_{2} = x(x — 1)\text{,}\) \(u_{3} = x(x — 1)(x — 2)\text{ ,}\) и т.
