Трапеция. Свойства и элементы трапеции
Виды трапеций
Равнобедренная трапеция — это вид трапеции с равными боковыми сторонами.
Также встречаются такие названия, как равнобокая или равнобочная.

Прямоугольная трапеция — это трапеция, у которой углы при боковой стороне прямые.

Элементы трапеции

a, b — основания трапеции (a параллельно b),
m, n — боковые стороны трапеции,
d1, d2 — диагонали трапеции,
h — высота трапеции (отрезок, соединяющий основания и при этом перпендикулярен им),
MN — средняя линия (отрезок, соединяющий середины боковых сторон).
Площадь трапеции

- Через полусумму оснований a, b и высоту h: S = \frac{a + b}{2}\cdot h
- Через среднюю линию MN и высоту h: S = MN\cdot h
- Через диагонали d1, d2 и угол (\sin \varphi) между ними: S = \frac{d_{1} d_{2} \sin \varphi}{2}
Свойства трапеции
Средняя линия трапеции
Средняя линия параллельна основаниям, равна их полусумме и разделяет каждый отрезок с концами, находящимися на прямых, которые содержат основания, (к примеру, высоту фигуры) пополам:
MN || a, MN || b, MN = \frac{a + b}{2}

Сумма углов трапеции
Сумма углов трапеции, прилежащих к каждой боковой стороне, равна 180^{\circ}:
\alpha + \beta = 180^{\circ}
\gamma + \delta =180^{\circ}

Равновеликие треугольники трапеции
Равновеликими, то есть имеющими равные площади, являются отрезки диагоналей и треугольники AOB и DOC, образованные боковыми сторонами.

Подобие образованных треугольников трапеции
Подобными треугольниками являются AOD и COB, которые образованы своими основаниями и отрезками диагоналей.
\triangle AOD \sim \triangle COB
Коэффициент подобия k находится по формуле:
k = \frac{AD}{BC}
Причем отношение площадей этих треугольников равно k^{2}.

Отношение длин отрезков и оснований
Каждый отрезок, соединяющий основания и проходящий через точку пересечения диагоналей трапеции, поделен этой точкой в отношении:
\frac{OX}{OY} = \frac{BC}{AD}
Это будет являться справедливым и для высоты с самими диагоналями.

Описанная около трапеции окружность
Каждая равнобокая трапеция может содержать описанную окружность. Только равнобокую трапецию возможно вписать в окружность.

Вписанная в трапецию окружность
Треугольники AOB и DOC являются прямоугольными, если трапеция ABCD описана около окружности. Центром же вписанной окружности будет являться точка O.
Опущенные на гипотенузы, высоты этих треугольников, тождественны радиусу вписанной окружности, а высота трапеции тождественна диаметру вписанной окружности.

academyege.ru
Трапеция
\[{\Large{\text{Произвольная трапеция}}}\]
Определения
Трапеция – это выпуклый четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.
Параллельные стороны трапеции называются её основаниями, а две другие стороны – боковыми сторонами.
Высота трапеции – это перпендикуляр, опущенный из любой точки одного основания к другому основанию.
Теоремы: свойства трапеции
1) Сумма углов при боковой стороне равна \(180^\circ\).
2) Диагонали делят трапецию на четыре треугольника, два из которых подобны, а два другие – равновелики.
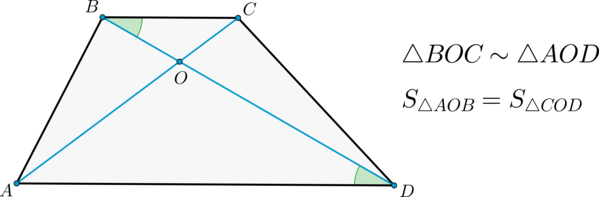
Доказательство
1) Т.к. \(AD\parallel BC\), то углы \(\angle BAD\) и \(\angle ABC\) – односторонние при этих прямых и секущей \(AB\), следовательно, \(\angle BAD +\angle ABC=180^\circ\).
2) Т.к. \(AD\parallel BC\) и \(BD\) – секущая, то \(\angle DBC=\angle
BDA\) как накрест лежащие.
Также \(\angle BOC=\angle AOD\) как вертикальные.
Следовательно, по двум углам \(\triangle BOC \sim \triangle AOD\).
Докажем, что \(S_{\triangle AOB}=S_{\triangle COD}\). Пусть \(h\) – высота трапеции. Тогда \(S_{\triangle ABD}=\frac12\cdot h\cdot AD=S_{\triangle ACD}\). Тогда: \[S_{\triangle AOB}=S_{\triangle ABD}-S_{\triangle AOD}=S_{\triangle ACD}-S_{\triangle AOD}=S_{\triangle COD}\]
Определение
Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.
Теорема
Средняя линия трапеции параллельна основаниям и равна их полусумме.

Доказательство*
С доказательством рекомендуется ознакомиться после изучения темы “Подобие треугольников”.
1) Докажем параллельность.

Проведем через точку \(M\) прямую \(MN’\parallel AD\) (\(N’\in CD\)). Тогда по теореме Фалеса (т.к. \(MN’\parallel AD\parallel BC, AM=MB\)) точка \(N’\) — середина отрезка \(CD\). Значит, точки \(N\) и \(N’\) совпадут.
2) Докажем формулу.
Проведем \(BB’\perp AD, CC’\perp AD\). Пусть \(BB’\cap MN=M’, CC’\cap MN=N’\).

Тогда по теореме Фалеса \(M’\) и \(N’\) — середины отрезков \(BB’\) и \(CC’\) соответственно. Значит, \(MM’\) – средняя линия \(\triangle ABB’\), \(NN’\) — средняя линия \(\triangle DCC’\). Поэтому: \[MM’=\dfrac12 AB’, \quad NN’=\dfrac12 DC’\]
Т.к. \(MN\parallel AD\parallel BC\) и \(BB’, CC’\perp AD\), то \(B’M’N’C’\) и \(BM’N’C\) – прямоугольники. По теореме Фалеса из \(MN\parallel AD\) и \(AM=MB\) следует, что \(B’M’=M’B\). Значит, \(B’M’N’C’\) и \(BM’N’C\) – равные прямоугольники, следовательно, \(M’N’=B’C’=BC\).
Таким образом:
\[MN=MM’+M’N’+N’N=\dfrac12 AB’+B’C’+\dfrac12 C’D=\] \[=\dfrac12 \left(AB’+B’C’+BC+C’D\right)=\dfrac12\left(AD+BC\right)\]
Теорема: свойство произвольной трапеции
Середины оснований, точка пересечения диагоналей трапеции и точка пересечения продолжений боковых сторон лежат на одной прямой.

Доказательство*
С доказательством рекомендуется ознакомиться после изучения темы “Подобие треугольников”.
1) Докажем, что точки \(P\), \(N\) и \(M\) лежат на одной прямой.

Проведем прямую \(PN\) (\(P\) – точка пересечения продолжений боковых сторон, \(N\) – середина \(BC\)). Пусть она пересечет сторону \(AD\) в точке \(M\). Докажем, что \(M\) – середина \(AD\).
Рассмотрим \(\triangle BPN\) и \(\triangle APM\). Они подобны по двум углам (\(\angle APM\) – общий, \(\angle PAM=\angle PBN\) как соответственные при \(AD\parallel BC\) и \(AB\) секущей). Значит: \[\dfrac{BN}{AM}=\dfrac{PN}{PM}\]
Рассмотрим \(\triangle CPN\) и \(\triangle DPM\). Они подобны по двум углам (\(\angle DPM\) – общий, \(\angle PDM=\angle PCN\) как соответственные при \(AD\parallel BC\) и \(CD\) секущей). Значит: \[\dfrac{CN}{DM}=\dfrac{PN}{PM}\]
Отсюда \(\dfrac{BN}{AM}=\dfrac{CN}{DM}\). Но \(BN=NC\), следовательно, \(AM=DM\).
2) Докажем, что точки \(N, O, M\) лежат на одной прямой.

Пусть \(N\) – середина \(BC\), \(O\) – точка пересечения диагоналей. Проведем прямую \(NO\), она пересечет сторону \(AD\) в точке \(M\). Докажем, что \(M\) – середина \(AD\).
\(\triangle BNO\sim \triangle DMO\) по двум углам (\(\angle OBN=\angle ODM\) как накрест лежащие при \(BC\parallel AD\) и \(BD\) секущей; \(\angle BON=\angle DOM\) как вертикальные). Значит: \[\dfrac{BN}{MD}=\dfrac{ON}{OM}\]
Аналогично \(\triangle CON\sim \triangle AOM\). Значит: \[\dfrac{CN}{MA}=\dfrac{ON}{OM}\]
Отсюда \(\dfrac{BN}{MD}=\dfrac{CN}{MA}\). Но \(BN=CN\), следовательно, \(AM=MD\).
\[{\Large{\text{Равнобедренная трапеция}}}\]
Определения
Трапеция называется прямоугольной, если один из ее углов – прямой.
Трапеция называется равнобедренной, если ее боковые стороны равны.
Теоремы: свойства равнобедренной трапеции
1) У равнобедренной трапеции углы при основании равны.
2) Диагонали равнобедренной трапеции равны.
3) Два треугольника, образованные диагоналями и основанием, являются равнобедренными.
Доказательство
1) Рассмотрим равнобедренную трапецию \(ABCD\).
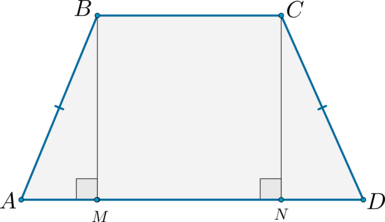
Из вершин \(B\) и \(C\) опустим на сторону \(AD\) перпендикуляры \(BM\) и \(CN\) соответственно. Так как \(BM\perp AD\) и \(CN\perp AD\), то \(BM\parallel CN\); \(AD\parallel BC\), тогда \(MBCN\) – параллелограмм, следовательно, \(BM = CN\).
Рассмотрим прямоугольные треугольники \(ABM\) и \(CDN\). Так как у них равны гипотенузы и катет \(BM\) равен катету \(CN\), то эти треугольники равны, следовательно, \(\angle DAB = \angle CDA\).
2) 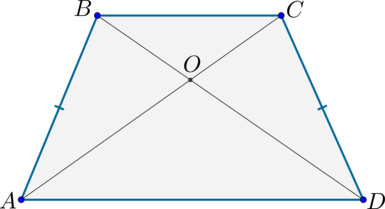
Т.к. \(AB=CD, \angle A=\angle D, AD\) – общая, то по первому признаку \(\triangle ABD=\triangle ACD\). Следовательно, \(AC=BD\).
3) Т.к. \(\triangle ABD=\triangle ACD\), то \(\angle BDA=\angle CAD\). Следовательно, треугольник \(\triangle AOD\) – равнобедренный. Аналогично доказывается, что и \(\triangle BOC\) – равнобедренный.
Теоремы: признаки равнобедренной трапеции
1) Если у трапеции углы при основании равны, то она равнобедренная.
2) Если у трапеции диагонали равны, то она равнобедренная.
Доказательство
Рассмотрим трапецию \(ABCD\), такую что \(\angle A = \angle D\).

Достроим трапецию до треугольника \(AED\) как показано на рисунке. Так как \(\angle 1 = \angle 2\), то треугольник \(AED\) равнобедренный и \(AE = ED\). Углы \(1\) и \(3\) равны как соответственные при параллельных прямых \(AD\) и \(BC\) и секущей \(AB\). Аналогично равны углы \(2\) и \(4\), но \(\angle 1 = \angle 2\), тогда \(\angle 3 = \angle 1 = \angle 2 = \angle 4\), следовательно, треугольник \(BEC\) тоже равнобедренный и \(BE = EC\).
В итоге \(AB = AE — BE = DE — CE = CD\), то есть \(AB = CD\), что и требовалось доказать.
2) Пусть \(AC=BD\). Т.к. \(\triangle AOD\sim \triangle BOC\), то обозначим их коэффициент подобия за \(k\). Тогда если \(BO=x\), то \(OD=kx\). Аналогично \(CO=y \Rightarrow AO=ky\).

Т.к. \(AC=BD\), то \(x+kx=y+ky \Rightarrow x=y\). Значит \(\triangle AOD\) – равнобедренный и \(\angle OAD=\angle ODA\).
Таким образом, по первому признаку \(\triangle ABD=\triangle ACD\) (\(AC=BD, \angle OAD=\angle ODA, AD\) – общая). Значит, \(AB=CD\), чтд.
shkolkovo.net
Трапеция. Свойства, признаки трапеции | Подготовка к ЕГЭ по математике
Трапеция – четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна).

Параллельные стороны трапеции называются основаниями. Другие две — боковые стороны.
Если боковые стороны равны, трапеция называется равнобедренной.

Трапеция, у которой есть прямые углы при боковой стороне, называется прямоугольной.

Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.

Свойства трапеции
1. Средняя линия трапеции параллельна основаниям и равна их полусумме.

2. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.

3. Треугольники  и
и  , образованные отрезками диагоналей и основаниями трапеции, подобны.
, образованные отрезками диагоналей и основаниями трапеции, подобны.
Коэффициент подобия – 
Отношение площадей этих треугольников есть  .
.

4. Треугольники  и
и  , образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь.
, образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь.

5. В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.

6. Отрезок, соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии.

7. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.

8. Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.

Свойства и признаки равнобедренной трапеции
1. В равнобедренной трапеции углы при любом основании равны.

2. В равнобедренной трапеции длины диагоналей равны.
3. Если трапецию можно вписать в окружность, то трапеция – равнобедренная.

4. Около равнобедренной трапеции можно описать окружность.
5. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.

Вписанная окружность
Если в трапецию вписана окружность с радиусом  и она делит боковую сторону точкой касания на два отрезка —
и она делит боковую сторону точкой касания на два отрезка —  и
и  , то
, то 

Площадь
 или
или  где
где  – средняя линия
– средняя линия

Смотрите хорошую подборку задач с трапецией (входят в ГИА и часть В ЕГЭ) здесь и здесь.
Смотрите также площадь трапеции.
egemaximum.ru
Трапеция — это… Что такое Трапеция?
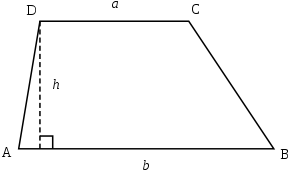
Трапе́ция (от др.-греч. τραπέζιον — «столик»; τράπεζα — «стол, еда») — четырёхугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна). Две параллельные стороны называются основанием трапеции, а две другие — это боковые стороны. Иногда трапеция определяется как четырёхугольник, у которого пара противолежащих сторон параллельна (про другую не уточняется), в этом случае параллелограмм является частным случаем трапеции. В частности, существует понятие криволинейная трапеция.
Связанные определения
Элементы трапеции
- Параллельные стороны называются основаниями трапеции.
- Две другие стороны называются боковыми сторонами.
- Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.
- Расстояние между основаниями называется высотой трапеции.
Виды трапеций
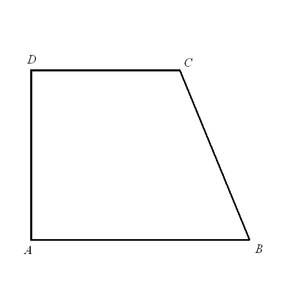 Прямоугольная трапеция
Прямоугольная трапеция 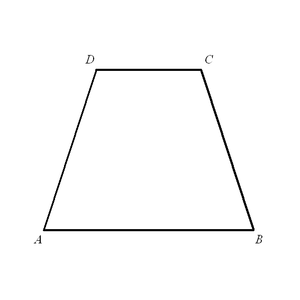 Равнобедренная трапеция
Равнобедренная трапеция- Трапеция, у которой боковые стороны равны, называется равнобокой или равнобедренной.
- Трапеция, имеющая прямые углы при боковой стороне, называется прямоугольной.
Общие свойства
- Средняя линия трапеции параллельна основаниям и равна их полусумме.
- Отрезок, соединяющий середины диагоналей, равен полуразности оснований.
- (Обобщённая теорема Фалеса). Параллельные прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки.
- В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.
Свойства и признаки равнобедренной трапеции
- Прямая, проходящая через середины оснований, перпендикулярна основаниям и является осью симметрии трапеции.
- Высота, опущенная из вершины на большее основание, делит его на два отрезка, один из которых равен полусумме оснований, другой — полуразности оснований.
- В равнобедренной трапеции углы при любом основании равны.
- В равнобедренной трапеции длины диагоналей равны.
- Если трапецию можно вписать в окружность, то она равнобедренная.
- Около равнобедренной трапеции можно описать окружность.
- Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.
Вписанная и описанная окружность
Площадь
- Здесь приведены формулы, свойственные именно трапеции. См. также формулы для площади произвольных четырёхугольников.
- В случае, если и — основания и — высота, формула площади:
- В случае, если — средняя линия и — высота, формула площади:
ɴʙ Эти формулы — одинаковы, так как полусумма оснований равняется средней линии трапеции:
- Формула, где , — основания, и — боковые стороны трапеции:
- Площадь равнобедренной трапеции с радиусом вписанной окружности, равным , и углом при основании :
- В частности, если угол при основании равен 30°, то:
- .
См. также
Примечания
dic.academic.ru
Трапеция. Видеоурок. Геометрия 8 Класс
Данный урок посвящён ещё одному специфическому виду четырёхугольников – трапециям. Как и в параллелограмме, в трапеции две стороны параллельны. Однако существенным отличием является то, что две другие стороны трапеции являются непараллельными. То есть параллелограмм не является частным случаем трапеции. Вместе с тем, несмотря на менее строгие условия в определении, трапеция обладает целым рядом интересных свойств. Кроме того, существует несколько видов трапеции – равнобедренная или равнобокая, прямоугольная трапеция. В школьном курсе геометрии очень много задач, в которых фигурирует трапеция. Поэтому изучение и понимание данной темы является необходимым для успешного освоения геометрии.
Тема: Четырехугольники
Урок: Трапеция
Определение
Трапеция – это четырёхугольник, у которого две стороны параллельны, а две другие – нет.
На Рис. 1. изображена произвольная трапеция.  – это боковые стороны (те, которые не параллельны).
– это боковые стороны (те, которые не параллельны). 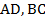 – основания (параллельные стороны).
– основания (параллельные стороны).
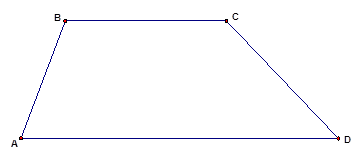
Рис. 1. Трапеция
Если сравнивать трапецию с параллелограммом, то у параллелограмма две пары параллельных сторон. То есть параллелограмм не является частным случаем трапеции, так как в определении трапеции чётко сказано, что две стороны трапеции не параллельны.
Выделим некоторые виды трапеции (частные случаи):
- равнобедренная (равнобокая) трапеция: боковые стороны равны;
- прямоугольная трапеция: один из углов равен
 (из определения трапеции и свойства параллельных прямых следует, что два угла будут по
(из определения трапеции и свойства параллельных прямых следует, что два угла будут по  ).
).
Определение
Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.
На Рис. 2. изображена трапеция со средней линией 
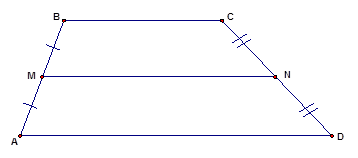
Рис. 2. Средняя линия трапеции
Свойства средней линии трапеции:
1. Средняя линия трапеции параллельна основаниям трапеции.
Доказательство:
Пусть середина боковой стороны 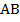 трапеции
трапеции 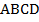 – точка
– точка 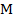 . Проведём через эту точку прямую, параллельную основаниям. Эта прямая пересечёт вторую боковую сторону трапеции
. Проведём через эту точку прямую, параллельную основаниям. Эта прямая пересечёт вторую боковую сторону трапеции 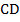 в точке
в точке 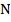 .
.
По построению:  . По теореме Фалеса из этого следует:
. По теореме Фалеса из этого следует:  . Значит,
. Значит, 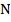 – середина стороны
– середина стороны 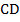 . Значит,
. Значит,  – средняя линия.
– средняя линия.
Доказано.
2. Средняя линия трапеции равна полусумме оснований трапеции: 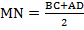 .
.
Доказательство:
Проведём среднюю линию трапеции и одну из диагоналей: например,  (см. Рис. 3).
(см. Рис. 3).
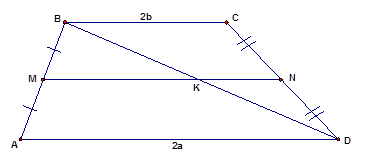
Рис. 3
По теореме Фалеса параллельные прямые отсекают на сторонах угла пропорциональные отрезки. Так как равны отрезки: 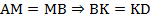 . Значит, отрезок
. Значит, отрезок  является средней линией треугольника
является средней линией треугольника  , а отрезок
, а отрезок 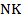 – средней линией треугольника
– средней линией треугольника  .
.
Значит, 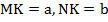 .
.
Примечание: это следует из свойства средней линии треугольника: средняя линия треугольника параллельна основанию и равна его половине. Первая часть этого свойства доказывается аналогично с доказательством первого свойства средней линии трапеции, а вторую часть можно доказать (к примеру, для средней линии  треугольника
треугольника  ), проведя через точку
), проведя через точку 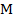 прямую, параллельную
прямую, параллельную  . Из теоремы Фалеса будет следовать, что эта прямая будет являться средней линией, а образованный четырёхугольник – параллелограммом (две пары попарно параллельных сторон). Отсюда уже несложно получить требуемое свойство.
. Из теоремы Фалеса будет следовать, что эта прямая будет являться средней линией, а образованный четырёхугольник – параллелограммом (две пары попарно параллельных сторон). Отсюда уже несложно получить требуемое свойство.
Получаем:  .
.
Доказано.
Рассмотрим теперь подробнее основные виды трапеции и их свойства.
Напомним, что равнобедренная трапеция – трапеция, у которой боковые стороны равны. Рассмотрим свойства боковой трапеции.
1. Углы при основании равнобедренной трапеции равны.
Доказательство:
Выполним стандартное дополнительное построение, которое очень часто используется при решении различных задач на трапецию: проведём прямую  параллельно боковой стороне
параллельно боковой стороне 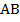 (см. Рис. 4).
(см. Рис. 4).
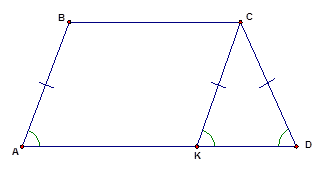
Рис. 4
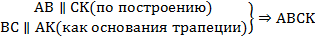 – параллелограмм.
– параллелограмм.
Отсюда следует, что:  . Значит, треугольник
. Значит, треугольник  – равнобедренный. А значит, углы при его основании равны, то есть:
– равнобедренный. А значит, углы при его основании равны, то есть:  (последние два угла равны, как соответственные при параллельных прямых
(последние два угла равны, как соответственные при параллельных прямых  ).
).
Доказано.
2. Диагонали равнобедренной трапеции равны.
Доказательство:
Для доказательства этого свойства воспользуемся предыдущим. Действительно, рассмотрим треугольники:  и
и  (см. Рис. 5.).
(см. Рис. 5.).
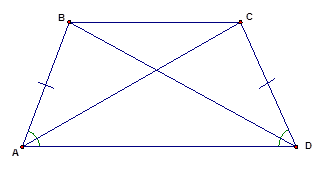
Рис. 5
 (по первому признаку равенства треугольников: две стороны и угол между ними).
(по первому признаку равенства треугольников: две стороны и угол между ними).
Из этого равенства сразу следует, что: 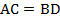 .
.
Доказано.
Оказывается, что, как и в случае с параллелограммом, у равнобедренной трапеции свойства одновременно являются и признаками. Сформулируем и докажем эти признаки.
Признаки равнобедренной трапеции
1. Дано: 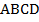 – трапеция;
– трапеция; 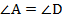 .
.
Доказать: 
Доказательство:
Доказательство данного признака абсолютно аналогично доказательству соответствующего свойства. Проведём в трапеции 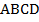 прямую
прямую  параллельно стороне
параллельно стороне 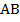 (см. Рис. 6).
(см. Рис. 6).
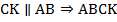 – параллелограмм (две пары попарно параллельных сторон).
– параллелограмм (две пары попарно параллельных сторон).
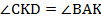 (соответственные углы при параллельных прямых). Откуда, пользуясь условием, получаем:
(соответственные углы при параллельных прямых). Откуда, пользуясь условием, получаем:  – равнобедренный
– равнобедренный

Рис. 6
(равны углы при основании). Значит:  (у параллелограмма противоположные стороны равны).
(у параллелограмма противоположные стороны равны).
Доказано.
2. Дано: 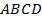 – трапеция;
– трапеция;  .
.
Доказать: 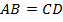 .
.
Доказательство:
Выполним ещё одно стандартное дополнительное построение при решении задач с трапецией: проведём через вершину 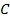 прямую
прямую  параллельно диагонали
параллельно диагонали  (см. Рис. 7).
(см. Рис. 7).
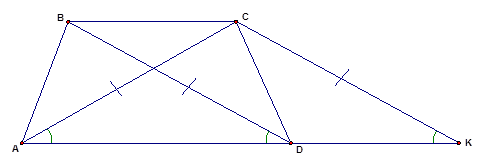
Рис. 7
 – параллелограмм (две пары попарно параллельных сторон).
– параллелограмм (две пары попарно параллельных сторон).
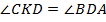 (соответственные углы при параллельных прямых). Кроме того,
(соответственные углы при параллельных прямых). Кроме того,  – равнобедренный (
– равнобедренный (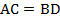 – по условию;
– по условию; 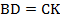 – по свойству параллелограмма). А значит:
– по свойству параллелограмма). А значит:  .
.
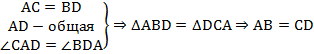
Доказано.
Рассмотрим несколько примеров решения задач с трапецией.
Пример 1.
Дано: 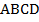 – трапеция;
– трапеция; 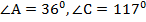 .
.
Найти: 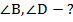
Решение:
Сумма углов при боковой стороне трапеции равна  – свойство внутренних односторонних углов при параллельных прямых. Из этого факта можно получить два равенства:
– свойство внутренних односторонних углов при параллельных прямых. Из этого факта можно получить два равенства:

Ответ:  .
.
Пример 2.
Дано: 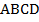 – трапеция;
– трапеция;  .
.  .
.
Найти:
interneturok.ru
Выбор одежды по типу фигуры
Как правильно подобрать одежду по типу фигуры — правильные советы, которые помогают
Автор статьи
Анна Турецкая
Время на чтение: 7 минут
АА
 Все женщины без исключения мечтают об идеальной фигуре, чтобы можно было носить самую разнообразную одежду. Но, как известно, идеал в природе встречается нечасто, и поэтому представительницам прекрасного пола приходится идти на всевозможные ухищрения, чтобы сделать свою фигуру лучше – хотя бы визуально. Сегодня мы поговорим о том, как правильно подобрать одежду к своему типу фигуры.
Все женщины без исключения мечтают об идеальной фигуре, чтобы можно было носить самую разнообразную одежду. Но, как известно, идеал в природе встречается нечасто, и поэтому представительницам прекрасного пола приходится идти на всевозможные ухищрения, чтобы сделать свою фигуру лучше – хотя бы визуально. Сегодня мы поговорим о том, как правильно подобрать одежду к своему типу фигуры.
Содержание статьи:
Основные типы женских фигур
 В конструировании женской одежды выделяют четыре основных типа женских фигур:
В конструировании женской одежды выделяют четыре основных типа женских фигур:
- Трапеция, конический тип, грушевидный (бёдра заметно шире плеч, талия ярко выражена).
- Треугольник (плечи заметно шире бедер).
- Прямоугольник, или плоский тип (плечи и бедра пропорциональны, талия не выражена).
- Песочные часы, округлый тип (плечи и бедра пропорциональны, ярко выражена талия).
Как правильно подобрать одежду к типу фигуры трапеция
 Женщинам с такой фигурой подойдёт одежда с полуприлеганием. Такому типу фигуры совершенно противопоказана прилегающая, обтягивающая одежда, так как она только подчеркнет недостатки. Прямых фасонов одежды женщинам с данным типом фигуры необходимо избегать, так как они сделают силуэт очень тяжелым, с массивным низом.
Женщинам с такой фигурой подойдёт одежда с полуприлеганием. Такому типу фигуры совершенно противопоказана прилегающая, обтягивающая одежда, так как она только подчеркнет недостатки. Прямых фасонов одежды женщинам с данным типом фигуры необходимо избегать, так как они сделают силуэт очень тяжелым, с массивным низом.
Читайте также: Маленькое черное платье для полных женщин — как выбрать свой фасон?
Юбка
Юбки женщинам с типом фигуры трапеция рекомендуется выбирать с длиной ниже колен, расклешенные, трапециевидные или с клиньями. Юбка должна обязательно расширяться книзу, можно носить юбки, скроенные по косой. Цвет юбки лучше выбирать чёрный, серый, коричневый – все неяркие, желательно тёмные цвета. Женщина должна избегать больших принтов на юбке, декоративной строчки на бедрах, пояса на бедрах. Если женщина всё же хочет носить узкую юбку, юбку-карандаш, то к ней обязательно необходимо подбирать удлиненные кардиганы или туники, скрывающие широкую часть бедер. Женщине можно обратить внимание на костюм с укороченным или полуприлегающим жакетом, он выгодно подчеркнет достоинства и скроет недостатки фигуры.
Брюки или джинсы
Как правильно выбрать брюки с учетом фигуры? Женщинам с трапециевидным типом фигуры нельзя носить брюки, широкие на бедрах, потому что они дополнительно увеличат и без того широкие бедра. Лучше всего в этой ситуации подойдут полуприлегающие брюки классического кроя, с прямой линией штанины, можно слегка зауженные или расширенные к щиколотке. Но сильно зауженных книзу брюк, особенно при широком крое на бедрах, женщинам с типом фигуры «трапеция» необходимо избегать, так как они сильно увеличат и без того массивные бедра. Женщины могут обратить внимание на брючный костюм, в котором брюки выполнены в классическом крое, а жакет свободного кроя с полуприлеганием (но не прямой), длиной до линии паха. Цвета для брючного костюма необходимо выбирать спокойные, темные – чёрный, серый, тёмно-синий, коричневый. Джинсы предпочтительно тёмных тонов покупать необходимо прямые, можно – с чуть заниженной линией талии. В брюках и джинсах показан клёш от середины бедра.
Блузки, кофточки, туники.
Эти вещи в гардеробе женщины с трапециевидным типом фигуры должны быть предпочтительно светлых тонов (носить их необходимо с тёмным низом, чтобы выровнять неравновесие фигуры). Блузки, кофточки лучше покупать однотонные, пастельных тонов.
Платье
Платье такой женщине необходимо выбирать приталенное. Поскольку от бедер необходимо отвлекать внимание, нужно сделать акцент на груди в виде интересного выреза, украшений, оригинального воротника, отделки, клапанов и карманов. Платья (как и блузки) можно выбирать розового, сиреневого, белого, голубого, светло-зеленого оттенков. Платья женщинам с типом фигуры «трапеция» лучше всего выбирать из летящих, струящихся, лёгких тканей, которые отлично драпируются и не создают объёма.
Аксессуары
Женщине с трапециевидной фигурой лучше отказаться от использования ремней и поясов. Если всё же женщина хочет использовать ремешки в гардеробе, предпочтение следует отдавать самым узким, и надевать их на платья или туники с полуприлеганием, свободно, не утягивая талию очень сильно. В обуви следует избегать массивности, каблук может быть шпилькой, или небольшим аккуратным каблучком средней длины. Балетки носить не рекомендуется.
Тип фигуры треугольник – подбираем одежду правильно
 Женщинам с таким типом фигуры необходимо делать акцент в одежде на талию и бедра. Верх одежды предпочтительно выбирать темных тонов, а низ – более светлых, можно ярких, со смелыми принтами.
Женщинам с таким типом фигуры необходимо делать акцент в одежде на талию и бедра. Верх одежды предпочтительно выбирать темных тонов, а низ – более светлых, можно ярких, со смелыми принтами.
Блузки, кофточки, туники, джемперы
Эти вещи в гардеробе женщины с типом фигуры «треугольник» должны иметь не горизонтальные, а вертикальные полоски. Показаны большие узоры. Вырез лучше иметь V-образный, карманы должны быть довольно большими. Жакеты лучше выбирать не прямые, а приталенные. Тона в одежде должны преобладать холодные: темно-синие, бордово-красные, зеленые.
Брюки и джинсы
Женщинам с типом фигуры «треугольник» можно носить брюки любого кроя. Хорошо будут смотреться джинсы светлых тонов, светлые брюки, брючный костюм с вертикальной полоской.
Юбки
Длина юбок для женщин с таким типом фигуры может быть любой – главное, чтобы ноги позволяли носить короткие или длинные юбки. Ткани лучше выбирать светлых, тёплых тонов, очень хорошо, если на ней будет косая полоска или клетка. На юбках могут быть также самые разнообразные принты, узоры, рисунок, кружева, клапаны и карманы.
Аксессуары
Ремень женщине с треугольным типом фигуры лучше выбирать широкий, и носить его необходимо с широкой юбкой или брюками. Из украшений следует предпочесть различные длинные бусы и цепи, довольно массивные кулоны, спускающиеся почти до талии.
Правильный выбор одежды для прямоугольного типа фигуры
 Женщинам этого типа необходимо сделать акцент на талии, создать стройный силуэт, правильные пропорции, подчеркнув достоинства деталями одежды. От широкой одежды следует отказаться, отдавая предпочтение полуприлегающим силуэтам. Необходимо выбирать геометрический узор в одежде, но не волнистые линии. В одежде следует избегать отворотов, извилистых швов, большой рассеченности по горизонтали в принтах или в крое одежды.
Женщинам этого типа необходимо сделать акцент на талии, создать стройный силуэт, правильные пропорции, подчеркнув достоинства деталями одежды. От широкой одежды следует отказаться, отдавая предпочтение полуприлегающим силуэтам. Необходимо выбирать геометрический узор в одежде, но не волнистые линии. В одежде следует избегать отворотов, извилистых швов, большой рассеченности по горизонтали в принтах или в крое одежды.
Блузки, топы, кофточки, жакеты.
Блузки и кофточки должны иметь длину чуть ниже талии, быть слегка приталенными, можно – с баской ниже талии. Рукава не нужно делать широкими. Очень хорошо этим женщинам будет рукав покроя «реглан». Жакеты необходимо покупать прямого кроя, ни в коем случае не чрезмерно укороченные. Верх лучше выдерживать в довольно сочных оттенках – красный, синий, зеленый, а также кремовом, тёплом бежевом. Жакеты этим женщинам можно выбирать в стиле «шанель». Жакеты, кардиганы и пальто можно выбирать короткие, или длинные прямые. Женщинам невысокого роста можно носить короткие жакеты, обувь на довольно высоких каблуках.
Юбки
Юбки представительницам треугольного типа фигуры необходимо приобретать или шить без пояса, с заниженной посадкой, их цвет должен сочетаться с верхней частью одежды.
Платья
Платья этим женщинам подойдут на бретельках, с прямым вырезом. Нельзя надевать платья-трапеции, платья-баллоны, потому что они зрительно увеличат область талии, а, следовательно – припишут женщине килограммы, которых у неё нет и в помине. Женщинам с прямоугольным типом фигуры можно надевать облегающие платья, а также платья рубашечного кроя, платья в стиле «сафари». Круглого глубокого выреза лучше всего избегать. Вырез на платьях и блузках должен быть V-образным, овальным или квадратным. Зрительно уменьшить талию поможет пышный лиф и пышная юбка на платье.
Брюки и джинсы
В брюках женщине с прямоугольным типом фигуры необходимо избегать любых крайностей – слишком широких или слишком узких, чрезмерно ярких и т.д. Если ноги красивые, женщина вполне может себе позволить носить брюки-капри.
Аксессуары
Пояса и ремешки женщине прямоугольного типа фигуры лучше не носить, потому что они будут только выделять проблему. Талию необходимо подчёркивать только кроем одежды. Обувь должна быть на каблуке средней длины, на платформе или плоской подошве, в зависимости от типа выбранного комплекта одежды. Если женщина хочет всё-таки надевать ремень, то следует выбирать его с пряжкой геометрической формы, а сверху на блузку надевать жакет или тунику, прикрывающие ремень с боков, для зрительного уменьшения талии.
Лучший выбор одежды для женщин с типом фигуры песочные часы
 Обладательницы данного типа фигуры могут себе позволить надевать всё, что угодно, им всё будет хорошо и к месту. В одежде необходимо избегать чрезмерного объёма – вещи должны иметь чёткую форму, иначе все достоинства фигуры просто затеряются под складками материи.
Обладательницы данного типа фигуры могут себе позволить надевать всё, что угодно, им всё будет хорошо и к месту. В одежде необходимо избегать чрезмерного объёма – вещи должны иметь чёткую форму, иначе все достоинства фигуры просто затеряются под складками материи.
Брюки и джинсы
Брючный гардероб женщины с типом фигуры «песочные часы» должен иметь вещи с заниженной линией талии. Сильно широкие брюки будут хорошо смотреться лишь в сочетании с контрастной блузкой и ремнем, или же корсетом. Под синие джинсы классического покроя можно надевать кофточки и блузки сочных тонов – например, красные, зеленые. При стройных ногах на таких женщинах очень хорошо будут смотреться шорты.
Юбки и платья
Эти вещи в гардеробе обладательницы «округлого» типа фигуры могут быть абсолютно любыми. При стройности обладательницы хорошо будут платья и юбки мини. Юбки могут быть с завышенной талией, хорошо будет смотреться юбка-карандаш. На вечер женщина данного типа фигуры может надеть длинное платье с очень пышным низом.
Аксессуары
Что касается ремней, поясов, тонких ремешков на талии, то женщина с типом фигуры песочные часы может себе позволить носить всё, что она пожелает, без всяких ограничений. Её фигуру не испортит даже широкий и плотный пояс-кушак, который склонен скрывать талию. Каблуки эта женщина может выбирать любые – от очень низких каблуков до высоких шпилек.
Автор статьи
Анна Турецкая
Редактор рубрики «Мода», модный эксперт журнала Colady
Поделитесь с друзьями и оцените статью:www.colady.ru
Трапеция
Раздел содержит задачи по геометрии (раздел планиметрия) о трапециях. Если Вы не нашли решения задачи — пишите об этом на форуме. Курс наверняка будет дополнен.
Трапеция. Определение, формулы и свойства
Трапе́ция (от др.-греч. τραπέζιον — «столик»; τράπεζα — «стол, еда») — четырёхугольник, у которого ровно одна пара противолежащих сторон параллельна.Трапеция — четырёхугольник, у которого пара противолежащих сторон параллельна.
Примечание. В этом случае параллелограмм является частным случаем трапеции.
Параллельные противоположные стороны называются основаниями трапеции, а две другие — боковыми сторонами.
Трапеции бывают:
— разносторонние ;
— равнобокие;
— прямоугольные
.Красным и коричневым цветами обозначены боковые стороны, зеленым и синим — основания трапеции.
A — равнобокая (равнобедренная, равнобочная) трапеция
B — прямоугольная трапеция
C — разносторонняя трапеция
У разносторонней трапеции все стороны разной длины, а основания параллельны.
У равнобокой трапеции боковые стороны равны, а основания параллельны.
У прямоугольной трапеции основания параллельны, одна боковая сторона перпендикулярна основаниям, а вторая боковая сторона — наклонная к основаниям.
Свойства трапеции
- Средняя линия трапеции параллельна основаниям и равна их полусумме
- Отрезок, соединяющий середины диагоналей, равен половине разности оснований и лежит на средней линии. Его длина
- Параллельные прямые, пересекающие стороны любого угла трапеции, отсекают от сторон угла пропорциональные отрезки (см. Теорему Фалеса)
- Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой (см. также свойства четырехугольника)
- Треугольники, лежащие на основаниях трапеции, вершины которых являются точкой пересечения ее диагоналей являются подобными. Соотношение площадей таких треугольников равно квадрату соотношения оснований трапеции
- Треугольники, лежащие на боковых сторонах трапеции, вершины которых являются точкой пересечения ее диагоналей являются равновеликими (равными по площади)
- В трапецию можно вписать окружность, если сумма длин оснований трапеции равна сумме длин её боковых сторон. Средняя линия в этом случае равна сумме боковых сторон, делённой на 2 (так как средняя линия трапеции равна полусумме оснований)
- Отрезок, параллельный основаниям и проходящий через точку пересечения диагоналей, делится последней пополам и равен удвоенному произведению оснований, деленному на их сумму 2ab / (a +b) (Формула Буракова)
Углы трапеции
Углы трапеции бывают острые, прямые и тупые.Прямыми бывают только два угла.
У прямоугольной трапеции два угла прямые, а два других – острый и тупой. У других видов трапеций бывают: два острых угла и два тупых.
Тупые углы трапеции принадлежат меньшему по длине основанию, а острые – большему основанию.
Любую трапецию можно рассматривать как усеченный треугольник, у которого линия сечения параллельна основанию треугольника.
Важно. Обратите внимание, что таким способом (дополнительным построением трапеции до треугольника) могут решаться некоторые задачи про трапецию и доказываются некоторые теоремы.
Как найти стороны и диагонали трапеции
Нахождение сторон и диагоналей трапеции делают с помощью формул, которые приведены ниже:
В указанных формулах применяются обозначения, как на рисунке.
a — меньшее из оснований трапеции
b — большее из оснований трапеции
c,d — боковые стороны
h1h2 — диагонали
Сумма квадратов диагоналей трапеции равна удвоенному произведению оснований трапеции плюс сумма квадратов боковых сторон (Формула 2)
Площадь трапеции
где
a и b — параллельные основания трапеции
c и d — боковые стороны трапеции
m — средняя линия трапеции
r — радиус вписанной в трапецию окружности
S — площадь трапеции Содержание главы:
Ромб | Описание курса | Площадь трапеции
profmeter.com.ua

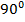 (из определения трапеции и свойства параллельных прямых следует, что два угла будут по
(из определения трапеции и свойства параллельных прямых следует, что два угла будут по 