Какие фигуры – Геометрические фигуры ◼️ виды с названиями, определение и обозначение, основные свойства, интересные факты о простых и сложных фигурах

Геометрические фигуры ◼️ виды с названиями, определение и обозначение, основные свойства, интересные факты о простых и сложных фигурах

Общая характеристика

Предметы в геометрическом изображении состоят из отдельных частей: точек, линий, лучей, отрезков и вершин. Отдельно взятый предмет имеет свое предназначение.

Основные понятия о составляющих

Когда все точки фигуры принадлежат одной плоскости, она является плоской. К ней относятся отрезок, прямоугольник. Существуют геометрические объекты, не являющиеся разновидностью плоскости, — куб, шар, пирамида, призма.

Минимальным объектом геометрии является точка. Определение того, какой она должна быть известно из школьного математического курса. Учебник характеризует ее как объект, не имеющий измерительных особенностей. Точка (Т) не содержит стандартных свойств: высоты, длины, радиуса, важным является только ее расположение. Обозначается числом или большой заглавной буквой. Например, точка называется D, E, F или 1, 2, 3. Несколько точек бывают отмечены разными цветами или буквами для удобного различия.

Линия состоит из множества точек. Измеряется длина этого составляющего объекта и обозначается маленькими буквами (abc).

Виды линий:

• Замкнутая. Когда в одной точке расположена начальная и конечная часть направления. Из незамкнутой линии получают обратный вариант.
• Разомкнутая. Начало и окончание не соединяются.
• Прямая. Обозначается буквой а или b.
• Ломаная. Заключается в соединенных отрезках не под углом 180 градусов. Линия обозначается перечислением всех вершин.
• Кривая.Отличная от прямой линии.

Задания из школьной программы кажутся школьникам скучными, неинтересным, но эти азы являются основой составления фигур простых и более сложных.

Существуют подвиды прямой линии: пересекающиеся, содержащие общую точку и когда две прямые линии соединяются в одной точке.

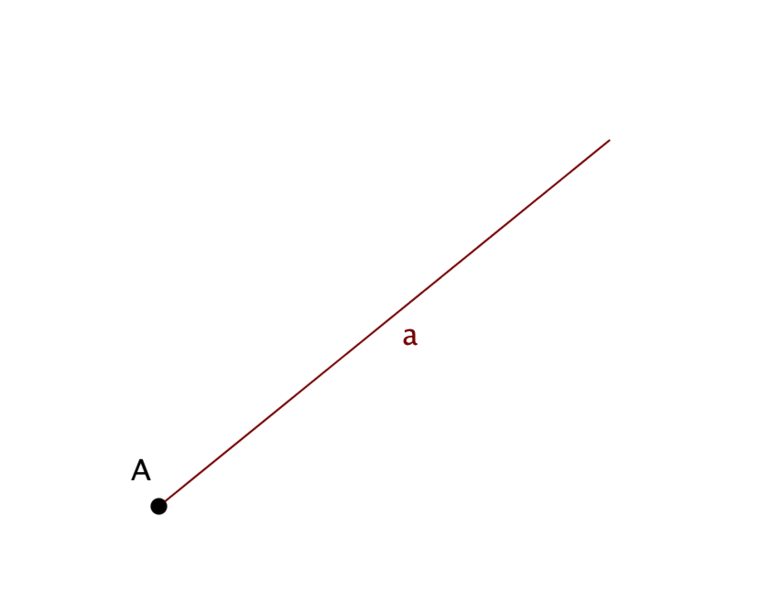
Луч в математике представляет часть прямой, имеющей начальную точку, но не имеющую конец. Это продолжение в одну сторону. Если Т разделяет линию пополам — получается два луча. Лучевые линии совпадают, когда расположены на одной прямой, начинаются в точке или направляются в одну сторону.

Отрезок представляет составную часть прямой, ограниченной двумя точками — она имеет начало и конец, поэтому измеряется. Длина отрезка представляет расстояние между его первой и последней точками. Через одну Т проводится бесконечное число линий, а через две — кривые и только одна прямая.

Стандартные объекты

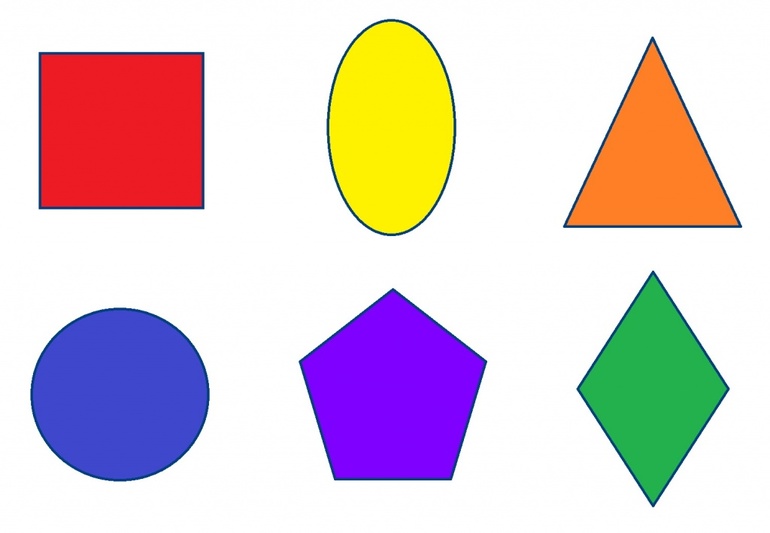
К основным фигурам геометрии на плоскости относятся прямоугольник, треугольник, квадрат, многоугольник и круг. Прямоугольник выглядит как фигура, состоящая из четырех сторон и четырех прямых углов (ПУ). Противоположные стороны равны между собой. В математике прямоугольник обозначается четырьмя латинским заглавными буквами. Все ПУ расположены под 90 градусов. Прямоугольник с равными, одинаковыми сторонами называется квадратом.

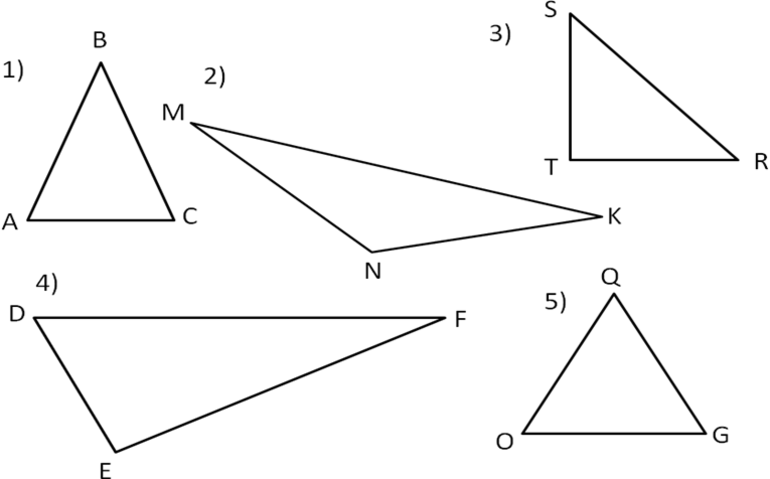
Фигура, имеющая 3 стороны и столько же углов (вершин), называется треугольником. Существует классификация этой фигуры по типу У.

Виды треугольника в зависимости от угла (У):

• Прямой. Один У будет прямым, два — менее 90 градусов.
• Острый. Градусная мера больше 0, но меньше 90 гр.
• Тупой. Один У тупой, два других будут острыми.

Геометрическая фигура с углами разной формы называется многоугольником. Его вершины представлены точками, соединяющими отрезками.

Радиус круга — промежуток от середины окружности до любой ее точки. Диаметр — это отрезок, соединяющий две точки окружности, проходящий через ее середину.

Параллелепипед — это призма, у которой основанием является параллелограмм. Когда все ребра параллелепипеда равны, получается куб.

Многогранная фигура, у которой одна грань является многоугольником, а остальные грани (боковые) — треугольники с общей вершиной, называется пирамидой.

Семиугольник (гептагон) — это многоугольник с 7 углами. Многоугольник представляет замкнутую ломанную линию.

Основные фигуры перечислены, но геометрия включает еще сложные объекты, использующиеся в различных областях жизни.

Сложные модели

В сложной геометрии выделяют фигуры с пространственным, плоским и объемным наполнением. Существует понятие геометрического тела, 3D-моделирование и проекция.

Определение тела и пространства

Геометрическое тело (ГТ) представляет часть пространства, отделенное замкнутой поверхностью наружной границы. Это понятие относится к компактному множеству точек, а две из них соединяют отрезком, проходящим внутри границы тела. Внешняя граница ГТ является его гранью, которых может быть несколько. Множество плоских граней определяет вершины и ребра ГТ. Все геометрические тела делятся на многогранники и тела вращения.

Тела вращения — объемные тела, образующиеся из-за вращения плоской фигуры, ограниченной кривой, вокруг оси. Эта ось расположена в той же плоскости. При вращении контуров фигур вокруг собственной оси возникает поверхность вращения, а если вращать заполненные контуры — возникают объекты (шар).

Шар представляет множество точек, расположенных от данной точки на небольшом пространстве. Точка является центром шара, а расстояние ограничено радиусом.

В сферу геометрии входят плоские (двухмерные) и объемные пространственные фигуры (трехмерные).

Плоские фигуры представляют точка, круг, полукруг, окружность, овал, прямоугольник, квадрат, луч, ромб, трапеция.

Существуют двухмерные фигуры (2D), представленные углом, многоугольником, четырехугольником, окружностью, кругом, эллипсом и овалом. Объекты 3D выделены двугранным или многогранным углом. Среди них известны призма, параллелепипед, куб, антипризма, пирамида, тетраэдр икосаэдр, бипирамида, геоид, эллипсоид, сфера шар и другие. Плоские фигуры изучает планиметрия, а объемные — стереометрия.

Объемные фигуры:

• Шар.
• Конус.
• Параллелепипед.
• Цилиндр.
• Сфера.

Конус образуется из треугольника с прямыми углами, при вращении его вокруг одного из катетов. Тороид возникает из замкнутой плоскости (окружности), вращающейся вокруг прямой и не пересекающей ее. Многогранник называется полиэдр, представляет замкнутую поверхность, состоящую из многоугольников.

Виды многогранников:

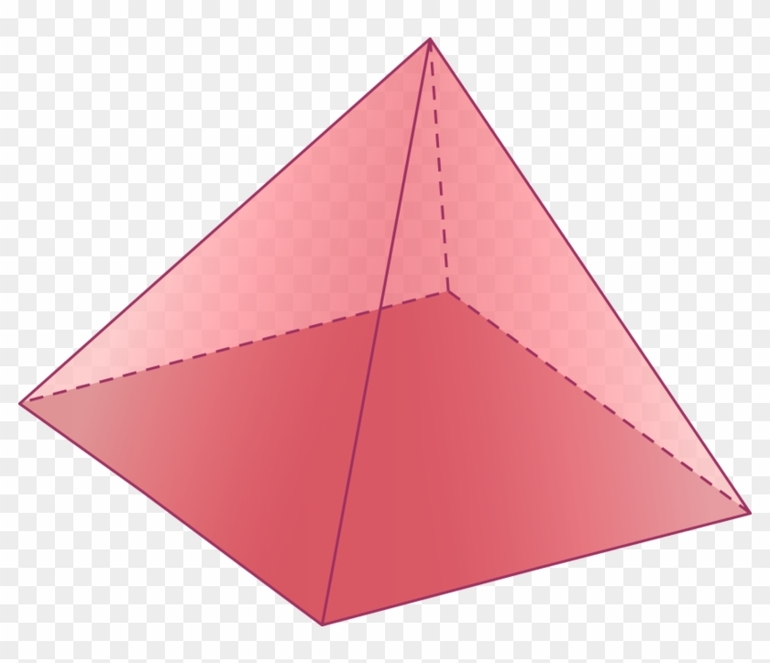
• Тетраэдер (четырехгранник). Это правильный треугольник.
• Куб (гексаэдр). Грани являются квадратом.
• Октаэдр. Имеется шесть вершин и восемь граней.
• Икосаэдр. Равносторонние треугольники являются гранями. Имеется 12 граней и 12 вершин.
• Додекаэдр. Правильные шестиугольники, имеется 12 граней, 20 вершин.

В школьной программе имеются специальные разделы геометрии, позволяющие распределить знания и не путать их в будущем. Это касается плоских, объемных фигур — одни изучает стереометрия, другие планиметрия.

Познавательные игрушки детям

Геометрия является наукой, которой можно знакомить детей с раннего возраста. Лучше распечатать картинки, геометрические фигуры для детей, затем нарисовать их вместе на чистом листе. Малышу первого года подобное занятие будет не очень интересным и понятным, а у дошкольника вызовет интерес, особенно если объекты изучения будут разноцветными или в необычном исполнении.

Основной материал для обучения детей:

• Яркие карточки с основными фигурами, формами. Шаблоны будут наглядным пособием перед школой.
• Раскраски, прописи, рабочая тетрадь. На каждой странице тетради представлены простейшие графические упражнения и задания. Выполняя их, малыш познакомится с геометрией и узнает названия фигур.
• Специальная детская литература.

Увлекательные, забавные, задорные стихи «Веселая геометрия для малышей» помогут детям быстро познакомиться и усвоить много важной информации о фигурах и размерах предметов. Веселые стишки помогут юному читателю соотнести малопонятные геометрические знания с обыденными предметами обихода. Например, в женской юбке представлена трапеция, в блюдце— круг, а в трубе цилиндр.

Учить детей начинают с плоских фигурок, сделанных из цветной бумаги или фетра. Не нужно ограничивать ребенка в фантазии, ведь он различает фигуры по цветам и форме — треугольник, овал, круг, ромб, квадрат. Увлекательным будет занятие с использованием сортеров, пирамидок из различных геометрических объектов.

Ближе к дошкольному возрасту переходят на объемные фигуры, кубики, конусы, кольца и цилиндры. В школьном возрасте знания накопятся, и дети будут осознанно различать равнобедренный, равносторонний треугольник, три понятия: луч, отрезок, окружность.

Раздел математики геометрия изучает пространственные отношения и формы. Фигура как понятие, рассмотренное во всех учебниках геометрии, является пространственной формой.

Геометрию можно обнаружить везде —

в любых окружающих предметах. Это современные здания, архитектурные строения, формы, космическая станция, интерьер квартиры, подводные лодки.

Математические знания являются профессионально важными для современных специальностей: дизайнеров и конструкторов, рабочих и ученых. Без знания основ геометрии невозможно построить здание или отремонтировать квартиру.

Картинки названия геометрических фигур (30 фото) • Прикольные картинки и позитив

Геометрические фигуры нужно знать для лучшего понимания предмета. Смотрите далее красивые картинки про названия геометрических фигур.
Прямоугольник, ромб, круг.
Параллелепипед, шар, конус.
Круг, квадрат, овал.
Сложные геометрические фигуры с названием.
Ломанная, многоугольник, отрезок.
Конус, цилиндр, сфера.
Картинка про название геометрических фигур.
Полукруг, треугольник, трапеция.
Квадраты, круги, овалы.
Разные фигуры из геометрии.
Параллелограмм, восьмиугольник.
Квадрат, шестиугольник, семиугольник.
Звезда, призма, сфера.
Предметная картинка про геометрические фигуры.
Большой красный конус.
Оранжевый ромб.
Синий куб.
Название геометрических фигур
Геометрические тела.
Разные пирамиды.
Простая картинка названия геометрических фигур.
Фиолетовый ромб.
Красивый конус.
Овал, трапеция, ромб.
Много фигур из учебника геометрии.
Куб, сфера.

Сердце, звезда, овал.
Геометрические фигуры и их названия.

Список правильных многомерных многогранников и соединений — Википедия

Примеры правильных многогранников

Правильные (2D) многоугольники
Выпуклые	Звёздчатые
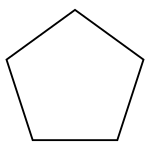{5}	{5/2}
Правильные 3D-многогранники
Выпуклые	Звёздчатые
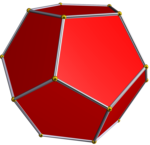{5,3}	{5/2,5}
Правильные 2D-замощения
Евклидовы	Гиперболические
{4,4}	{5,4}[en]
Правильные 4D-многогранники
Выпуклые	Звёздчатые
{5,3,3}	{5/2,5,3}[en]
Правильные 3D-замощения
Евклидовы	Гиперболические
{4,3,4}	{5,3,4}

Эта страница содержит список правильных многомерных многогранников (политопов) и правильных cоединений этих многогранников в евклидовом, сферическом и гиперболическом пространствах разных размерностей.

Символ Шлефли описывает каждое правильное замощение n-сферы, евклидова и гиперболического пространства. Символ Шлефли описания n-мерного многогранника равным образом описывает мозаику (n-1)-сферы. Вдобавок, симметрия правильного многогранника или замощения выражается как группа Коксетера, которые Коксетер обозначал идентично символам Шлефли, за исключением разграничения квадратными скобками, и эта нотация называется нотацией Коксетера^[en]. Другой связанный символ — диаграмма Коксетера — Дынкина, которая представляет группу симметрии (без помеченных кружком узлов) и правильные многогранники или замощения с обведённым кружком первым узлом. Например, куб имеет символ Шлефли {4,3}, с его октаэдральной симметрией^[en] [4,3] или , представляется диаграммой Коксетера .

Правильные многогранники сгруппированы по размерности, а затем по форме — выпуклые, невыпуклые и бесконечные. Невыпуклые виды используют те же вершины, что и выпуклые, но имеют пересекающиеся фасеты (грани максимальной размерности = размерности пространства – 1). Бесконечные виды замощают евклидово пространство на единицу меньшей размерности.

Бесконечные формы можно расширить до замощения гиперболического пространства. Гиперболическое пространство подобно обычному пространству, но параллельные прямые с расстоянием расходятся. Это позволяет вершинным фигурам иметь отрицательные угловые дефекты. Например, в вершине может сходиться семь правильных треугольников, лежащих на плоскости. Это нельзя осуществить на обычной (евклидовой) плоскости, но можно сделать при некотором масштабе на гиперболической плоскости.

Многогранники, удовлетворяющие более общему определению и не имеющие простых символов Шлефли, включают правильные косые многогранники и бесконечноугольные правильные косые многогранники с неплоскими фасетами или вершинными фигурами.

Таблица показывает сводку правильных многогранников по размерностям.

	Конечные			Евклидовы	Гиперболические			Соединения
Разм.	Выпук- лые	Звёзд- чатые	Косые	Выпук- лые	Компак- тные	Звёзд- чатые	Параком- пактные	Выпук- лые	Звёзд- чатые
1	1	0	0	1	0	0	0	0	0
2	∞	∞	∞	1	1	0	0	∞	∞
3	5	4	?	3	∞	∞	∞	5	0
4	6	10	?	1	4	0	11	26	20
5	3	0	?	3	5	4	2	0	0
6	3	0	?	1	0	0	5	0	0
7	3	0	?	1	0	0	0	3	0
8	3	0	?	1	0	0	0	6	0
9+	3	0	?	1	0	0	0	*	0

* 1, если размерность имеет вид 2^k − 1, 2, если размерность является степенью двойки, 0 в противном случае.

Не существует правильных звёздчатых замощений в евклидовом пространстве любой размерности.

Диаграмма Коксетера — Дынкина представляет зеркальные «плоскости» как узлы, и помещает кружок вокруг узла, если точка не лежит на плоскости. Отрезок, { }, — это точка p и зеркальный образ точки p, а также отрезок между ними.

Одномерный многогранник (1-многогранник) — это замкнутый отрезок, ограниченный двумя конечными точками. 1-многогранник является правильным по определению и представляется символом Шлефли { }^[1][2] или диаграммой Коксетера с единственным помеченным кружком узлом, . Норман Джонсон^[en] дал им название дайтел и символ Шлефли { } ^[3].

Будучи тривиальным в качестве многогранника, дайтел возникает в качестве рёбер многоугольников и многогранников^[4]. Он используется в определении однородных призм (как в символе Шлефли { }×{p}) или в диаграмме Коксетера как прямое произведение отрезка и правильного многоугольника ^[5].

Двумерное пространство (многоугольники)[править | править код]

Двумерные многогранники называются многоугольниками. Правильные многоугольники имеют равные стороны и вписаны в окружность. Правильный p-угольник представляется символом Шлефли {p}.

Обычно только выпуклые многоугольники считаются правильными, но звёздчатые многоугольники наподобие пентаграммы можно также считать правильными. Они используют те же вершины, что и выпуклые формы, но соединение происходит другим путём, при котором окружность обходится более одного раза.

Звёздчатые многоугольники следует называть скорее невыпуклыми, чем вогнутыми, поскольку пересечение рёбер не образует новых вершин и все вершины находятся на окружности.

Выпуклые[править | править код]

Символ Шлефли {p} представляет правильный p-угольник.

Название	Треугольник (2-симплекс)	Квадрат (2-ортоплекс) (2-куб)	Пятиугольник	Шестиугольник	Семиугольник	Восьмиугольник
Шлефли	{3}	{4}	{5}	{6}	{7}	{8}
Симметрия	D3, [3]	D4, [4]	D5, [5]	D6, [6]	D7, [7]	D8, [8]
Коксетер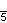
Рисунок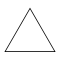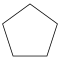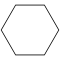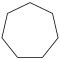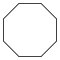
Название	Девятиугольник	Десятиугольник	Одиннадцатиугольник	Двенадцатиугольник	Тринадцатиугольник	Четырнадцатиугольник
Шлефли	{9}	{10}	{11}	{12}	{13}	{14}
Симметрия	D9, [9]	D10, [10]	D11, [11]	D12, [12]	D13, [13]	D14, [14]
Дынкин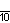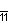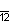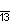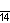
Рисунок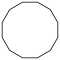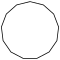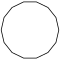
Название	Пятнадцатиугольник	Шестнадцатиугольник	Семнадцатиугольник	Восемнадцатиугольник	Девятнадцатиугольник	Двадцатиугольник	…p-угольник
Шлефли	{15}	{16}	{17}	{18}	{19}	{20}	{p}
Симметрия	D15, [15]	D16, [16]	D17, [17]	D18, [18]	D19, [19]	D20, [20]	Dp, [p]
Дынкин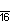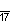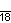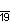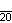
Рисунок

Сферические[править | править код]

Правильный двуугольник {2} можно считать вырожденным правильным многоугольником. Он может существовать как невырожденный в некоторых неевклидовых пространствах, таких как поверхность сферы или тора.

Звёзды[править | править код]

Существует бесконечно много правильных звёздчатых многогранников в двумерном пространстве (т.е. многоугольников), символы Шлефли которых являются рациональными числами {n/m}. Они называются звёздчатыми многоугольниками и имеют то же самое расположение вершин^[en], что и у выпуклого многоугольника.

В общем случае для любого натурального числа n и для всех m, таких, что m < n/2 и m, n взаимно просты, существуют n-точечные правильные звёзды с символами Шлефли {n/m} (строго говоря, {n/m}={n/(n−m)}) .

Пространственные многоугольники[править | править код]

В 3-мерном пространстве правильный пространственный многоугольник ^[6] называется антипризматическим многоугольником и он имеет то же расположение вершин^[en], что и у антипризмы, и его рёбра являются подмножеством рёбер антипризмы, соединяющие зигзагом вершины верхнего и нижнего многоугольников.

В 4-мерном пространстве правильный пространственный многоугольник может иметь вершины на торе Клиффорда и связан с вращением Клиффорда^[en]. В отличие от антипризматичных пространственных многоугольников, пространственные многоугольники двойного вращения могут иметь нечётное число сторон.

Их можно видеть в многоугольниках Петри выпуклых правильных четырёхмерных многогранников^[en], видимые как правильные плоские многоугольники периметров проекций Коксетера:

Трёхмерное пространство (многогранники)[править | править код]

В трёхмерном пространстве правильный многогранник с символом Шлефли {p,q} и диаграммой Коксетера имеет правильные грани вида {p} и правильную вершинную фигуру {q}.

Вершинная фигура (многогранника) является многоугольником, получаемым соединением вершин, отстоящих на одно ребро от заданной вершины. Для правильных трёхмерных многогранников, эта вершинная фигура является всегда правильным (и планарным) многоугольником.

Существование правильного многогранника {p,q} ограничено неравенством, относящимся к угловому дефекту вершинной фигуры:

1p+1q>12{\displaystyle {\frac {1}{p}}+{\frac {1}{q}}>{\frac {1}{2}}} : Многогранник (существует в евклидовом 3-мерном пространстве)

1p+1q=12{\displaystyle {\frac {1}{p}}+{\frac {1}{q}}={\frac {1}{2}}} : Евклидова плоская мозаика

1p+1q<12{\displaystyle {\frac {1}{p}}+{\frac {1}{q}}<{\frac {1}{2}}} : Замощение гиперболической плоскости

Перенумеровав перестановки, мы найдём 5 выпуклых форм, 4 звёздчатые формы и 3 плоских замощения, все с многоугольниками {p} и {q} из списка: {3}, {4}, {5}, {5/2} и {6}.

Вдобавок к мозаикам евклидова пространства существует бесконечное количество правильных гиперболических мозаик.

Выпуклые[править | править код]

Пять выпуклых правильных многогранников называются платоновыми телами. Вершинная фигура указана вместе с числом вершин. Все эти многогранники имеют эйлерову характеристику (χ) 2.

Геометрические фигуры и их названия

Здесь вы с ребенком можете изучить геометрические фигуры и их названия с помощью веселых заданий в картинках. Но обучение будет проходить наиболее эффективно в том случае, если к распечатанному заданию вы добавите еще и различные образцы геометрических фигур. Для этой цели могут подойти такие предметы, как мячики, пирамидки, кубики, надутые воздушные шары (круглые и овальные), кружки для чая (стандартные, в форме цилиндра), апельсины, книги, клубки ниток, квадратные печенья и многое другое — все, что подскажет вам фантазия.

Все перечисленные предметы помогут ребенку понять, что значит объемная геометрическая фигура. Плоские фигуры можно подготовить, вырезав из бумаги нужные геометрические формы, предварительно раскрасив их в разные цвета. 

Чем больше различных материалов вы подготовите для занятия, тем интереснее будет ребенку изучать новые для него понятия.

Также вам может понравиться наш онлайн тренажер по математике для 1 класса «Геометрические фигуры»:

Геометрические фигуры 1 класс — Онлайн-тренажер

Онлайн-тренажер по математике «Геометрические фигуры 1 класс» поможет первоклассникам потренироваться в умении различать основные геометрические фигуры: квадрат, круг, овал, прямоугольник и треугольник.

Геометрические фигуры и их названия — Проводим занятие с ребенком:

Чтобы легко и непринужденно ребенок смог запомнить геометрические фигуры и их названия, скачайте сначала картинку с заданием во вложениях внизу страницы, распечатайте на цветном принтере и положите на стол вместе с цветными карандашами. Также к этому времени у вас уже должны быть заготовлены различные предметы, которые мы перечисляли ранее.

• 1 этап. Сначала пусть ребенок выполнит задания на распечатанном листе — проговорит вслух названия фигур и раскрасит все картинки.
• 2 этап. Необходимо наглядно показать ребенку отличия объемных фигур от плоских. Для этого разложите все предметы-образцы (как объемные, так и вырезанные из бумаги) и отойдите с ребенком от стола на такое расстояние, с которого хорошо видны все объемные фигуры, но потерялись из виду все плоские образцы. Обратите внимание малыша на этот факт. Пусть он поэкспериментирует, подходя к столу то ближе, то дальше, рассказывая вам о своих наблюдениях.  
• 3 этап. Дальше занятие нужно превратить в своеобразную игру. Попросите ребенка, чтобы он внимательно посмотрел вокруг себя и нашел предметы, которые имеют форму каких-либо геометрических фигур. Например, телевизор — прямоугольник, часы — круг и т.д. На каждой найденной фигуре — громко хлопайте в ладоши, чтобы добавить энтузиазма в игру.
• 4 этап. Проведите исследовательскую и наблюдательную работу с теми материалами-образцами, которые вы заготовили к занятию. Например, положите на стол книгу и плоский прямоугольник из бумаги. Предложите ребенку пощупать их, посмотреть на них с разных сторон и рассказать вам свои наблюдения. Таким же образом можно исследовать апельсин и бумажный круг, детскую пирамидку и бумажный треугольник, кубик и бумажный квадрат, воздушный шар овальной формы и овал, вырезанный из бумаги. Список предметов вы можете дополнить сами.
• 5 этап. Положите в непрозрачный пакет различные объемные образцы и попросите ребенка достать на ощупь квадратный предмет, затем круглый, затем прямоугольный и так далее. 
• 6 этап. Разложите перед ребенком на столе несколько различных предметов из тех, которые участвуют в занятии. Затем пусть ребенок отвернется на несколько секунд, а вы спрячьте один из предметов. Повернувшись к столу ребенок должен назвать спрятанный предмет и его геометрическую форму.

 Скачать геометрические фигуры и их названия — Бланк задания — вы можете во вложениях внизу страницы.

Названия геометрических фигур — Карточки для распечатки

Изучая с малышом геометрические фигуры, вы можете использовать во время занятий карточки для распечатки от Лисёнка Бибуши. Скачайте вложения, распечатайте на цветном принтере бланк с карточками, вырежьте каждую карточку по контуру – и приступайте к обучению. Карточки можно заламинировать, либо наклеить на более плотную бумагу, чтобы сохранить внешний вид картинок, ведь использоваться они будут неоднократно.

Первые шесть карточек дадут вам возможность изучить с ребенком такие фигуры: овал, круг, квадрат, ромб, прямоугольник и треугольник, под каждой фигурой в карточках можно прочесть ее название.

После того, как ребенок запомнил название определенной фигуры, попросите его выполнить следующее: обвести по контуру все имеющиеся на карточке образцы изучаемой фигуры, а затем раскрасить их в цвет основной фигуры, расположенной в верхнем левом углу.

Скачать названия геометрических фигур — Карточки для распечатки — вы можете во вложениях внизу страницы

Карточки для распечатки с изображением плоских геометрических фигур

С помощью следующих шести карточек ребенок сможет познакомиться с такими геометрическими фигурами: параллелограмм, трапеция, пятиугольник, шестиугольник, звезда и сердце. Как и в предыдущем материале под каждой фигурой можно найти ее название.

Чтобы разнообразить занятия с малышом, совмещайте обучение с рисованием – такой метод не даст ребенку переутомиться, и малыш с удовольствием будет продолжать учебу. Следите за тем, чтобы обводя фигуры по черточкам, ребенок не спешил и выполнял задание аккуратно, ведь подобные упражнения не только развивают мелкую моторику, они могут повлиять в дальнейшем на почерк малыша.

Скачать карточки для распечатки с изображением плоских геометрических фигур вы можете во вложениях

Объемные геометрические фигуры и их названия — скачать карточки

В процессе, того, как вы будете изучать с ребенком объемные геометрические фигуры и их названия, используя новые шесть карточек от Бибуши с изображениями куба, цилиндра, конуса, пирамиды, шара и полусферы, приобретите изучаемые фигуры в магазине, либо воспользуйтесь предметами, находящимися в доме, имеющими подобную форму.

Покажите малышу на примерах, как в жизни выглядят объемные фигуры, ребенок должен потрогать и поиграть с ними. Прежде всего, это необходимо для того, чтобы задействовать наглядно – действенное мышление малыша, с помощью которого ребенку проще познавать окружающий мир.

Скачать — Объемные геометрические фигуры и их названия — вы можете во вложениях внизу страницы

Также вам будут полезны и другие материалы по изучению геометрических фигур: 

Рисунки из геометрических фигур — Задания в картинках и раскраски

Веселые и красочные задания для детей «Рисунки из геометрических фигур» являются очень удобным обучающим материалом для детей дошкольного и младшего школьного возраста по изучению и запоминанию основных геометрических форм:

Геометрические фигуры — Раскраска для дошкольников

Задания ознакомят ребенка с основными фигурами геометрии — кругом, овалом, квадратом, прямоугольником и треугольником. Только здесь не занудное зазубривание названий фигур, а своеобразная игра-раскраска.

 

Плоские геометрические фигуры — Обведи и дорисуй

Как правило, геометрию начинают изучать, рисуя плоские геометрические фигуры. Восприятие правильной геометрической формы невозможно без выведения ее своими руками на листе бумаги.

Найди формы геометрических фигур в картинках

Это занятие изрядно позабавит ваших юных математиков. Ведь теперь им придется находить знакомые формы геометрических фигур среди множества картинок. 

 

Наложение фигур друг на друга — Задание для детей

Наложение фигур друг на друга — это занятие по геометрии для дошкольников и младших школьников. Смысл упражнения состоит в решении примеров на сложение. Только это необычные примеры. Вместо цифр здесь нужно складывать геометрические фигуры. 

Свойства геометрических фигур для дошкольников

Это задание составлено в виде игры, в которой ребенку предстоит менять свойства геометрических фигур: форму, цвет или размер.

 

Счет геометрических фигур — Картинки с заданиями

Здесь вы можете скачать задания в картинках, в которых представлен счет геометрических фигур для занятий по математике.

 

Чертежи геометрических тел — Задание для детей

В этом задании ребенок познакомится с таким понятием, как чертежи геометрических тел. По сути, это занятие представляет собой мини-урок по начертательной геометрии

Геометрические фигуры из бумаги — Вырезаем и занимаемся

Здесь мы подготовили для вас объемные геометрические фигуры из бумаги, которые нужно вырезать и склеить. Куб, пирамиды, ромб, конус, цилиндр, шестигранник,  распечатать их на картоне (или цветной бумаге, а затем наклеить на картон), а затем дать ребенку для запоминания. 

Счет до 5 — Картинки с заданиями для малышей

Здесь мы выложили для вас счет до 5 — картинки с математическими заданиями для малышей, благодаря которым ваши дети потренируют не только свои навыки счета, но и умение читать, писать, различать геометрические фигуры, рисовать и раскрашивать.

 

И еще можете поиграть в математические игры онлайн от лисенка Бибуши:

Игра «Что лишнее? — Геометрические формы»

В этой развивающей онлайн игре ребенку предстоит определить, что является лишним среди 4 картинок. При этом необходимо руководствоваться признаками геометрических форм.

 

Названия геометрических фигур в картинках (23 ФОТО) ⭐ Забавник

 

Объёмные геометрические фигуры

 

Разноцветные фигуры

 

Названия объёмных фигур на английском

 

Синие фигуры с английскими названиями

 

Синие фигуры с русскими названиями

 

Разноцветные фигуры с английскими названиями

 

Простые фигуры кубической сингонии

 

Куб, икосаэдр, тетраэдр, октаэдр, додекаэдр

 

Весёлые геометрические фигуры

 

Shapes

 

Конус

 

Треугольник, пятиугольник, шестиугольник, семиугольник, восьмиугольник

 

Ромб

 

Призмы

 

Пирамиды

 

 

 

 

Геометрическая фигура — Википедия

Материал из Википедии — свободной энциклопедии

У этого термина существуют и другие значения, см. Фигура. Фигуры на плоскости.

Геометрическая фигура (от лат. figura) — термин, формально применимый к произвольному множеству точек.

Обычно фигурой на плоскости называют замкнутые множества, которые ограничены конечным числом линий. При этом допускаются вырождения, например: угол, луч и точка считаются геометрическими фигурами.

Если все точки фигуры лежат в некоторой плоскости — она называется плоской и она может быть задана уравнением g(x,y)=0{\displaystyle g(x,y)=0}.

Порядок (степень) фигуры — это порядок (степень) уравнения, которым она задана.^[1]

Если Φ — фигура, состоящая из всех точек плоскости, удовлетворяющих уравнению f(x,y,z)=0{\displaystyle f(x,y,z)=0}, то данное уравнение — уравнение фигуры, оно задает фигуру Φ.^[1]

1. ↑ ^{1 2} Милованов М. В., Тышкевич Р. И., Феденко А. С. Часть 1 // Алгебра и аналитическая геометрия. — Минск: Вышэйшая школа, 1984. — С. 221. — 305 с.

Многоугольник — определение и основные понятия, виды и свойства фигур

Многоугольником называется геометрическая фигура, которая со всех сторон ограничена замкнутой ломаной линией. При этом количество звеньев ломаной не должно быть меньше трех. Каждая пара отрезков ломаной имеет общую точку и образует углы. Количество углов совместно с количеством отрезков ломаной являются основными характеристиками многоугольника. В каждом многоугольнике количество звеньев ограничивающей замкнутой ломаной совпадает с количеством углов.

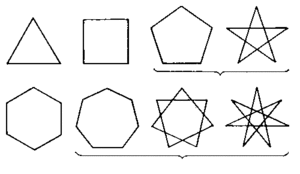
Сторонами в геометрии принято называть звенья ломаной линии, которая ограничивает геометрический объект. Вершинами называют точки соприкосновения двух соседних сторон, по количеству которых получают свои названия многоугольники.

Если замкнутая ломаная состоит из трех отрезков, она носит название треугольника; соответственно, из четырех отрезков — четырехугольником, из пяти — пятиугольником и пр.

Для обозначения треугольника или четырехугольника пользуются заглавными латинскими буквами, обозначающими его вершины. Буквы называют по порядку — по часовой стрелке или против нее.

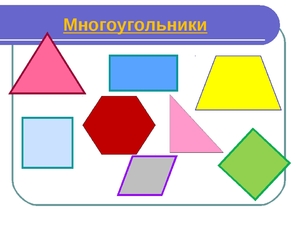
Основные понятия

Описывая определение многоугольника, следует учитывать некоторые смежные геометрические понятия:

1. Если вершины являются концами одной стороны, они называются соседними.
2. Если отрезок соединяет между собой несоседние вершины, то он имеет название диагонали. У треугольника не может быть диагоналей.
3. Внутренний угол — это угол при одной из вершин, который образован двумя его сторонами, сходящимися в этой точке. Он всегда располагается во внутренней области геометрической фигуры. Если многоугольник невыпуклый, его размер может превосходить 180 градусов.
4. Внешний угол при определенной вершине — это угол смежный с внутренним при ней же. Иными словами, внешним углом можно считать разность между 180° и величиной внутреннего угла.
5. Сумма величин всех отрезков носит название периметра.
6. Если все стороны и все углы равны — он носит название правильного. Правильными могут быть только выпуклые.

Как уже упоминалось выше, названия многоугольных геометрических строятся исходя из количества вершин. Если у фигуры их количество равняется n, она носит название n-угольника:

1. Многоугольник называется плоским, если ограничивает конечную часть плоскости. Эта геометрическая фигура может быть вписанной в окружность или описанной вокруг окружности.
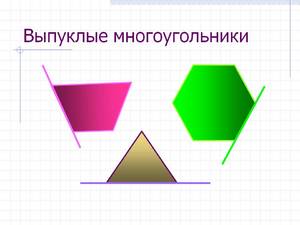
2. Выпуклым называется n-угольник, который соответствует одному из условий, приведенных ниже.
3. Фигура расположена по одну сторону от прямой линии, которая соединяет две соседних вершины.
4. Эта фигура служит общей частью или пересечением нескольких полуплоскостей.
5. Диагонали располагаются внутри многоугольника.
6. Если концы отрезка располагаются в точках, которые принадлежат многоугольнику, весь отрезок принадлежит ему.
7. Фигура может называться правильной, если у нее все отрезки и все углы равны. Примерами могут служить квадрат, равносторонний треугольник или правильный пятиугольник.
8. Если n-угольник невыпуклый, все стороны и углы его равны, а вершины совпали с таковыми правильного n-угольника, он называется звездчатым. У таких фигур могут иметься самопересечения. Примерами могут служить пентаграмма или гексаграмма.
9. Треугольник или четырехугольник называется вписанным в окружность, когда все его вершины располагаются внутри одной окружности. Если же стороны этой фигуры имеют точки соприкосновения с окружностью, это многоугольник описанным около некоторой окружности.

Любой выпуклый n-угольник можно поделить на треугольники. При этом количество треугольников бывает меньше количества сторон на 2.

Виды фигур

Треугольник

Это многоугольник с тремя вершинами и тремя отрезками, соединяющими их. При этом точки соединения отрезков не лежат на одной прямой.

Точки соединения отрезков — это вершины треугольника. Сами отрезки называются сторонами треугольника. Общая сумма внутренних углов каждого треугольника равняется 180°.

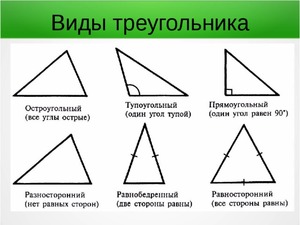
По соотношениям между сторонами все треугольники можно подразделять на несколько видов:

1. Равносторонние — у которых длина всех отрезков одинаковая.
2. Равнобедренные — треугольники, у которых равны два отрезка из трех.
3. Разносторонние — если длина всех отрезков разная.

Кроме того, принято различать следующие треугольники:

1. Остроугольные.
2. Прямоугольные.
3. Тупоугольные.

Четырехугольник

Четырехугольником называется плоская фигура, имеющая 4 вершины и 4 отрезка, которые их последовательно соединяют.

1. Если все углы четырехугольника прямые — эта фигура называется прямоугольником.
2. Прямоугольник, у которого все стороны имеют одинаковую величину, называется квадратом.
3. Четырехугольник, все стороны которого равны, называется ромбом.

На одной прямой не может находиться сразу три вершины четырехугольника.

Видео

Дополнительную информацию о многоугольниках вы найдете в этом видео.