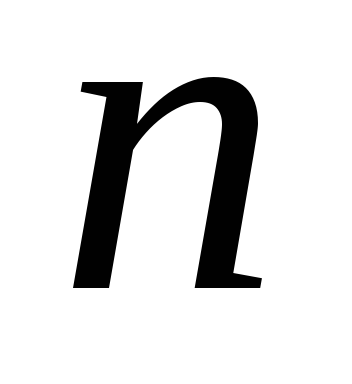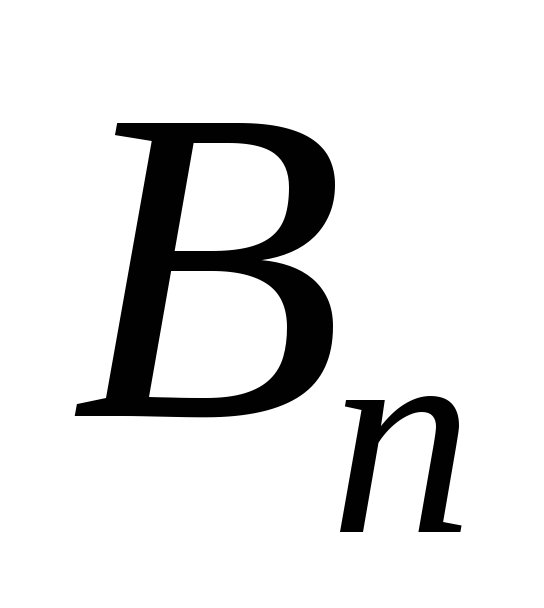Число Белла — Википедия
Материал из Википедии — свободной энциклопедии
Число Белла — число всех неупорядоченных разбиений n{\displaystyle n}-элементного множества, обозначаемое Bn{\displaystyle B_{n}}, при этом по определению полагают B0=1{\displaystyle B_{0}=1}.
Значения Bn{\displaystyle B_{n}} для n=0,1,2,…{\displaystyle n=0,1,2,\dots } образуют последовательность[1]:
- 1, 1, 2, 5, 15, 52, 203, 877, 4140, 21 147, 115 975, …
Число Белла можно вычислить как сумму чисел Стирлинга второго рода:
- Bn=∑m=0nS(n,m){\displaystyle B_{n}=\sum _{m=0}^{n}S(n,m)},
а также задать в рекуррентной форме:
- Bn+1=∑k=0n(nk)Bk{\displaystyle B_{n+1}=\sum _{k=0}^{n}{\binom {n}{k}}B_{k}}.
Для чисел Белла справедлива также формула Добинского[2]:
- Bn=1e∑k=0∞knk!{\displaystyle B_{n}={\frac {1}{e}}\sum _{k=0}^{\infty }{\frac {k^{n}}{k!}}}.
Если p{\displaystyle p} — простое, то верно сравнение Тушара:
- Bn+p≡Bn+Bn+1(modp){\displaystyle B_{n+p}\equiv B_{n}+B_{n+1}{\pmod {p}}}
и более общее:
- Bn+pm≡mBn+Bn+1(modp){\displaystyle B_{n+p^{m}}\equiv mB_{n}+B_{n+1}{\pmod {p}}}.
Экспоненциальная производящая функция чисел Белла имеет вид[3]:
- ∑n=0∞Bnn!xn=eex−1{\displaystyle \sum _{n=0}^{\infty }{\frac {B_{n}}{n!}}x^{n}=e^{e^{x}-1}}.
- Яблонский С. В. Введение в дискретную математику. — М.: Высшая школа, 2006. — 392 с. — ISBN 5-06-005683-X.
Числа Белла Википедия
Число Белла — число всех неупорядоченных разбиений n{\displaystyle n}-элементного множества, обозначаемое Bn{\displaystyle B_{n}}, при этом по определению полагают B0=1{\displaystyle B_{0}=1}.
Значения Bn{\displaystyle B_{n}} для n=0,1,2,…{\displaystyle n=0,1,2,\dots } образуют последовательность[1]:
- 1, 1, 2, 5, 15, 52, 203, 877, 4140, 21 147, 115 975, …
Число Белла можно вычислить как сумму чисел Стирлинга второго рода:
- Bn=∑m=0nS(n,m){\displaystyle B_{n}=\sum _{m=0}^{n}S(n,m)},
а также задать в рекуррентной форме:
- Bn+1=∑k=0n(nk)Bk{\displaystyle B_{n+1}=\sum _{k=0}^{n}{\binom {n}{k}}B_{k}}.
Для чисел Белла справедлива также формула Добинского[2]:
- Bn=1e∑k=0∞knk!{\displaystyle B_{n}={\frac {1}{e}}\sum _{k=0}^{\infty }{\frac {k^{n}}{k!}}}.
Если p{\displaystyle p} — простое, то верно сравнение Тушара:
- Bn+p≡Bn+Bn+1(modp){\displaystyle B_{n+p}\equiv B_{n}+B_{n+1}{\pmod {p}}}
и более общее:
- Bn+pm≡mBn+Bn+1(modp){\displaystyle B_{n+p^{m}}\equiv mB_{n}+B_{n+1}{\pmod {p}}}.
Экспоненциальная производящая функция чисел Белла имеет вид[3]:
- ∑n=0∞Bnn!xn=eex−1
Число Белла — Википедия. Что такое Число Белла
Материал из Википедии — свободной энциклопедииЧисло Белла — число всех неупорядоченных разбиений n{\displaystyle n}-элементного множества, обозначаемое Bn{\displaystyle B_{n}}, при этом по определению полагают B0=1{\displaystyle B_{0}=1}.
Значения Bn{\displaystyle B_{n}} для n=0,1,2,…{\displaystyle n=0,1,2,\dots } образуют последовательность[1]:
- 1, 1, 2, 5, 15, 52, 203, 877, 4140, 21 147, 115 975, …
Число Белла можно вычислить как сумму чисел Стирлинга второго рода:
- Bn=∑m=0nS(n,m){\displaystyle B_{n}=\sum _{m=0}^{n}S(n,m)},
а также задать в рекуррентной форме:
- Bn+1=∑k=0n(nk)Bk{\displaystyle B_{n+1}=\sum _{k=0}^{n}{\binom {n}{k}}B_{k}}.
Для чисел Белла справедлива также формула Добинского[2]:
- Bn=1e∑k=0∞knk!{\displaystyle B_{n}={\frac {1}{e}}\sum _{k=0}^{\infty }{\frac {k^{n}}{k!}}}.
Если p{\displaystyle p} — простое, то верно сравнение Тушара:
- Bn+p≡Bn+Bn+1(modp){\displaystyle B_{n+p}\equiv B_{n}+B_{n+1}{\pmod {p}}}
и более общее:
- Bn+pm≡mBn+Bn+1(modp){\displaystyle B_{n+p^{m}}\equiv mB_{n}+B_{n+1}{\pmod {p}}}.
Экспоненциальная производящая функция чисел Белла имеет вид[3]:
- ∑n=0∞Bnn!xn=eex−1{\displaystyle \sum _{n=0}^{\infty }{\frac {B_{n}}{n!}}x^{n}=e^{e^{x}-1}}.
Примечания 9
Литература
- Яблонский С. В. Введение в дискретную математику. — М.: Высшая школа, 2006. — 392 с. — ISBN 5-06-005683-X.
Числа Белла
Число Белла 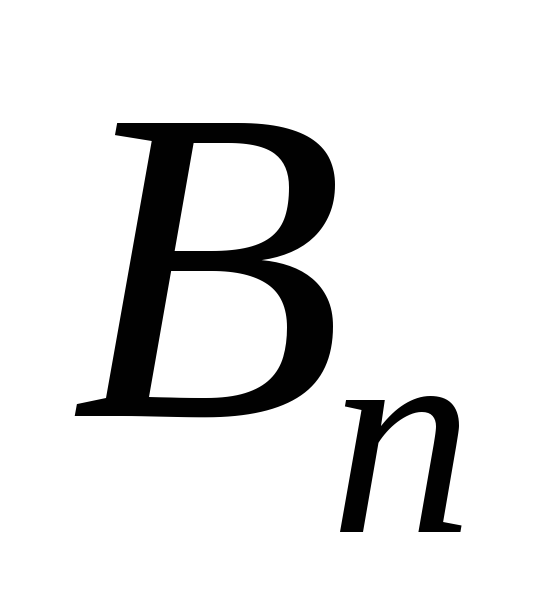 равно количеству разбиений множества
из
равно количеству разбиений множества
из  элементов на произвольное количество
непустых подмножеств, которые не
пересекаются. Очевидно, что
элементов на произвольное количество
непустых подмножеств, которые не
пересекаются. Очевидно, что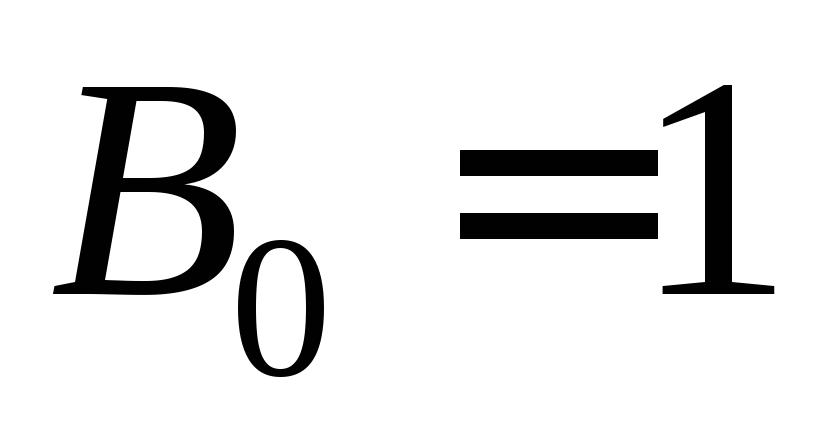 ,
так как существует только одно разбиение
пустого множества. Например,
,
так как существует только одно разбиение
пустого множества. Например,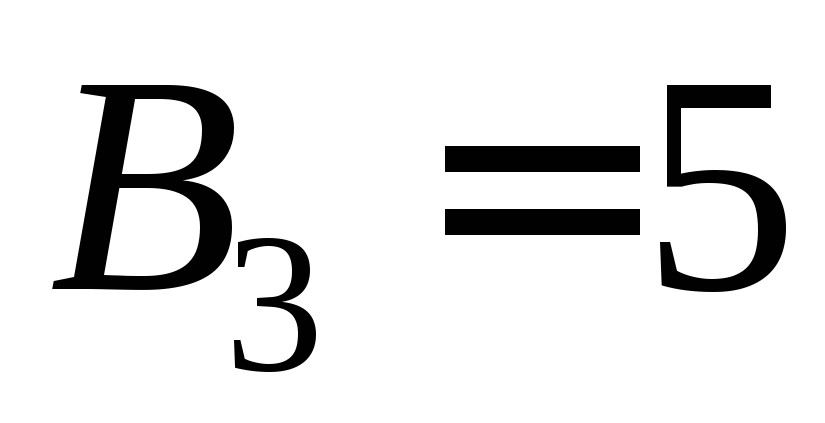 ,
так как существует 5 возможных разбиений
множества
,
так как существует 5 возможных разбиений
множества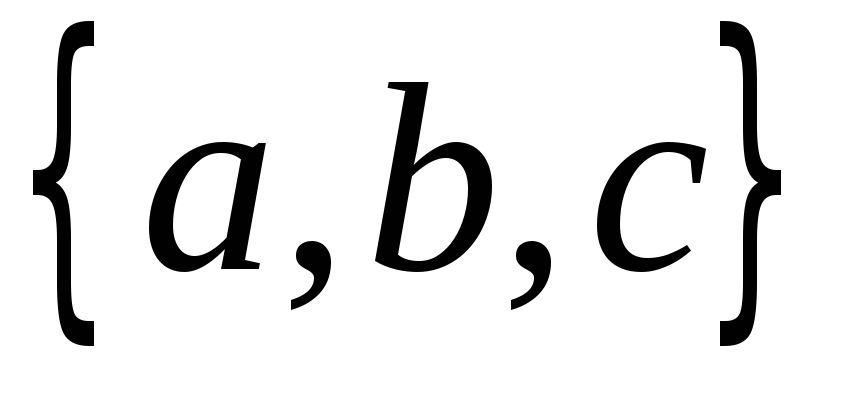
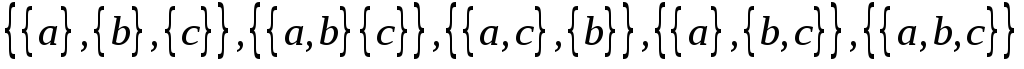
Заметим, что 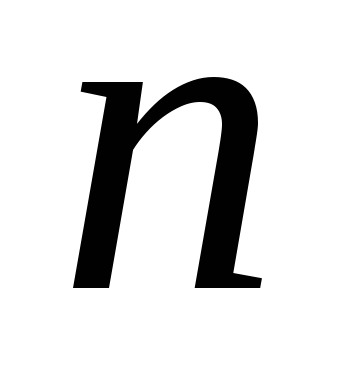 элементов можно разбить на
элементов можно разбить на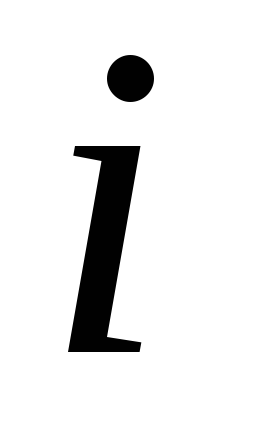 множеств
множеств .
При этом количество разбиений
.
При этом количество разбиений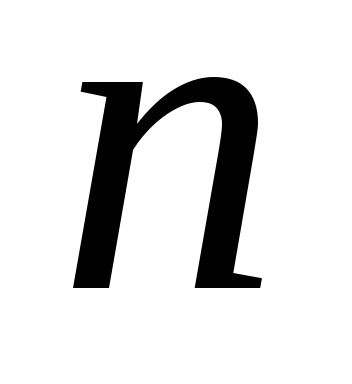 – элементного множества на
– элементного множества на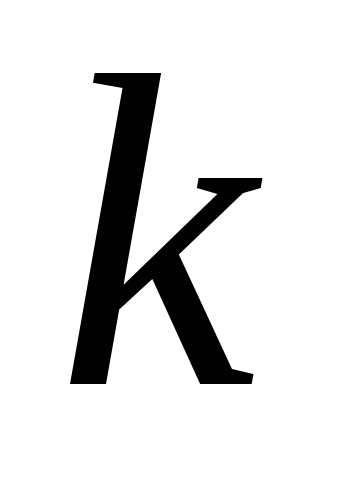 подмножеств равно числу Стирлинга 2
рода
подмножеств равно числу Стирлинга 2
рода .
Откуда получаем формулу:
.
Откуда получаем формулу:

| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 1 | 2 | 5 | 15 | 52 | 203 | 877 | 4140 | 21147 | 115975 |
Рассмотрим следующие
конструкции, в которых точки обозначают
одноэлементные множества, а сегменты
объединяют элементы, принадлежащие
одному множеству. Из 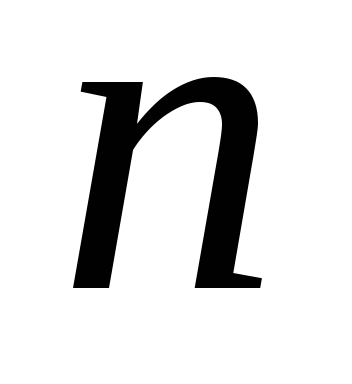 элементов можно построить
элементов можно построить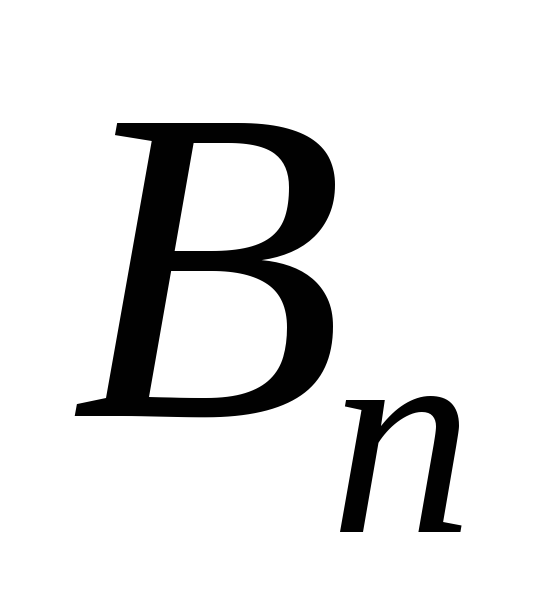 разных таких конструкций.
разных таких конструкций.
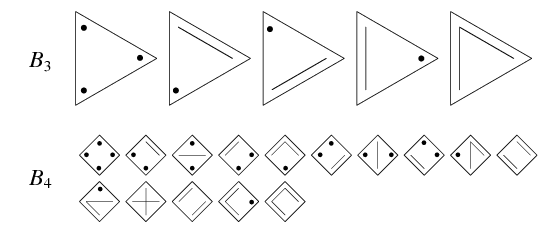
Теорема. Числа Белла удовлетворяют следующему рекуррентному соотношению:
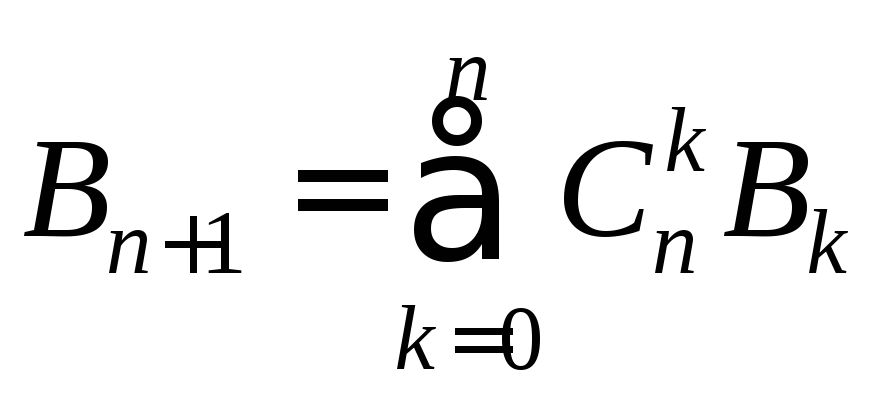
Доказательство. Рассмотрим разбиение  элемента в зависимости от величины
блока, в котором находится
элемента в зависимости от величины
блока, в котором находится –
ый элемнент. Пусть размер этого блока
равен
–
ый элемнент. Пусть размер этого блока
равен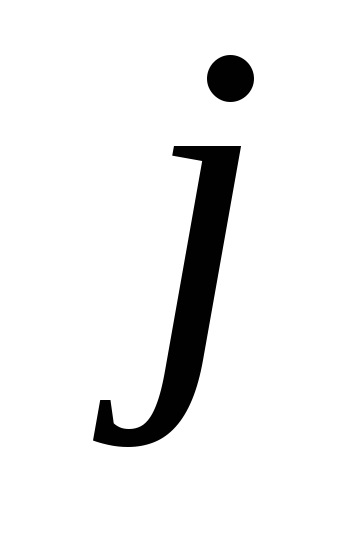
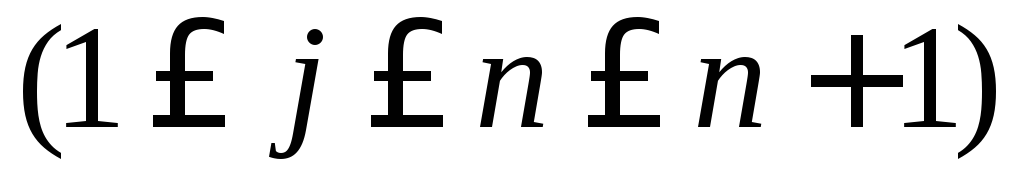 .
Тогда существует
.
Тогда существует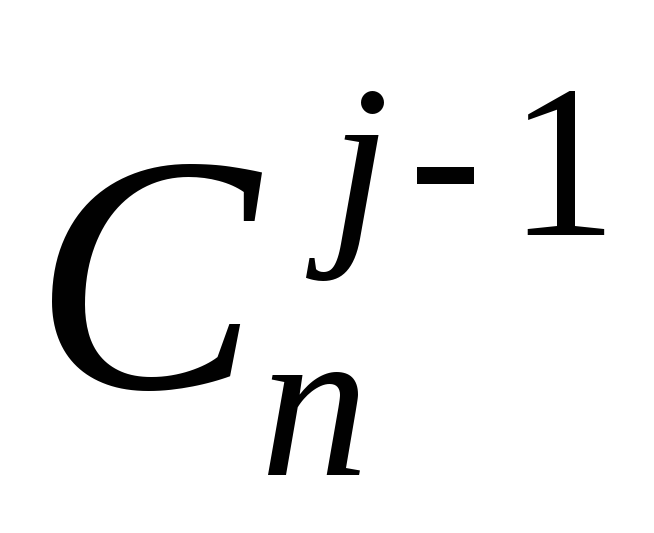 способов выбрать в него кроме
способов выбрать в него кроме –
ого еше
–
ого еше элемент. Остальные
элемент. Остальные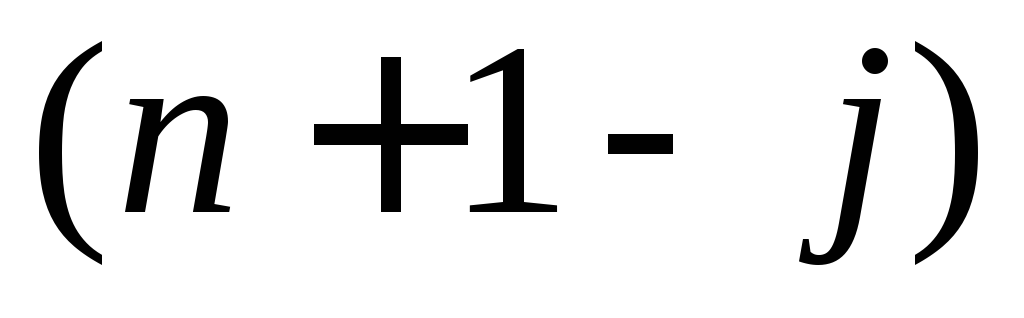
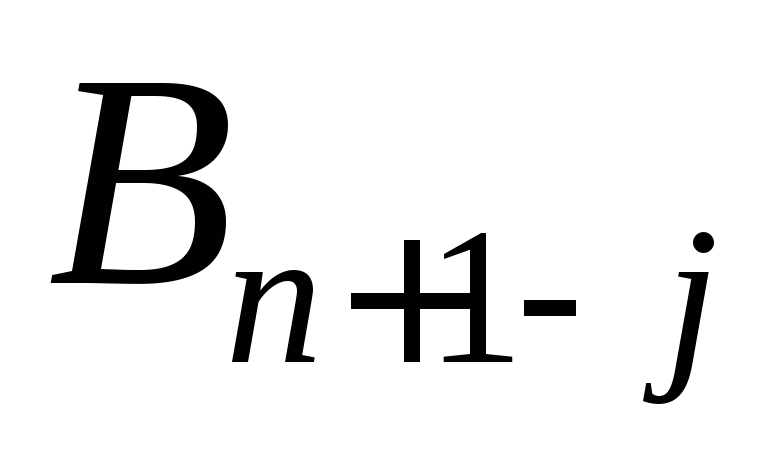 способами.Таким образом:
способами.Таким образом: 
Пример.Например, 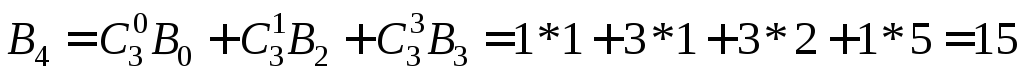 .
Числа Белла удовлетворяют следующему
свойству:
.
Числа Белла удовлетворяют следующему
свойству:

Для значений 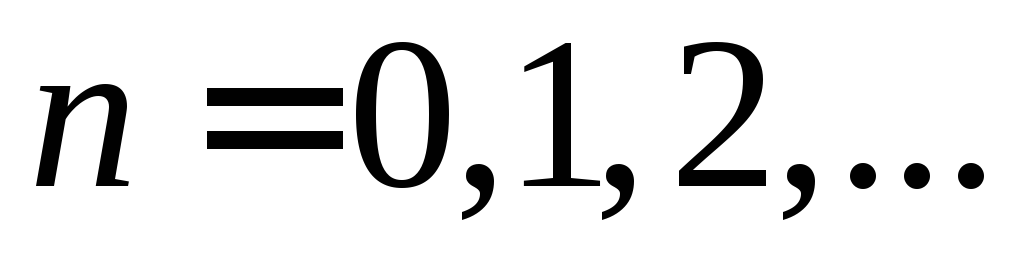 получим следующие значения детерминанта:
получим следующие значения детерминанта:
1, 1, 2, 12, 288, 34560, 24883200, 125411328000, 5056584744960000, 1834933472251084800000, 6658606584104736522240000000, …
При разложении функции 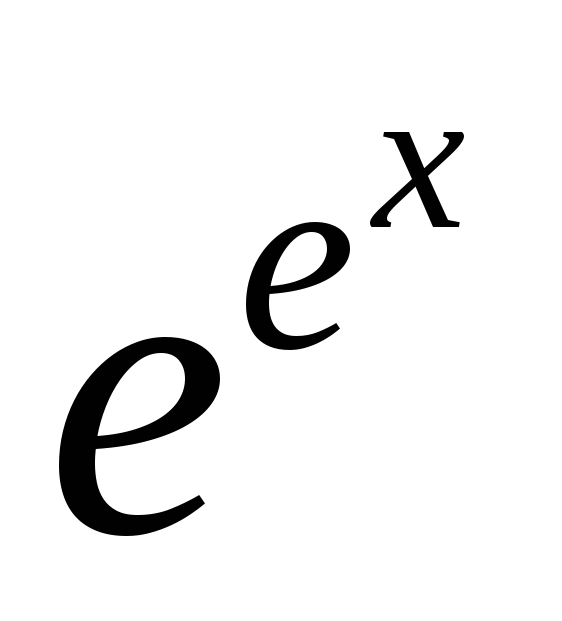

Числа  могут быть построены при помощитреугольника Белла.
Первая строка содержит 1. Каждая следующая
строка начинается числом, стоящим в
конце предыдущей строки. Каждое следующее
число в строке равно сумме чиел, стоящих
слева и сверху от него. Числа Белла
образуют последние числа в строках.
могут быть построены при помощитреугольника Белла.
Первая строка содержит 1. Каждая следующая
строка начинается числом, стоящим в
конце предыдущей строки. Каждое следующее
число в строке равно сумме чиел, стоящих
слева и сверху от него. Числа Белла
образуют последние числа в строках.

Композиции
При решении задач про распределение одинаковых предметов между
одинаковых предметов между
 в сумму натуральных слагаемых
в сумму натуральных слагаемых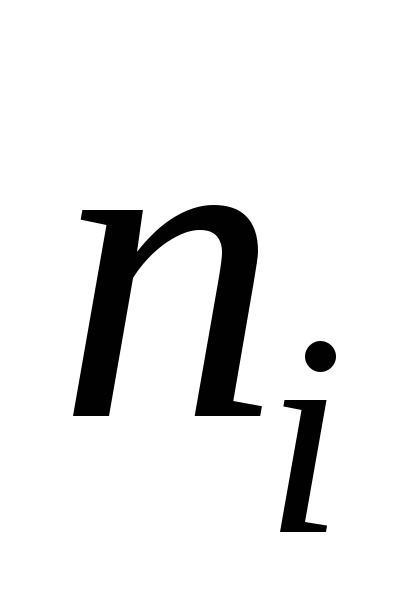 :
: 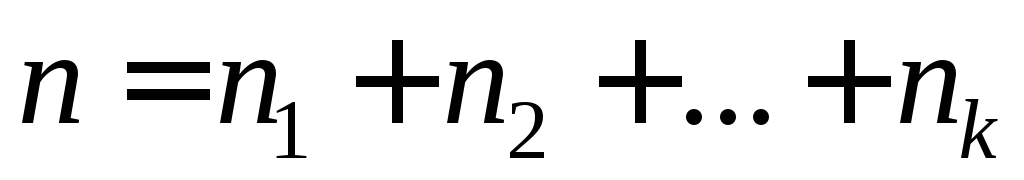 , где
, где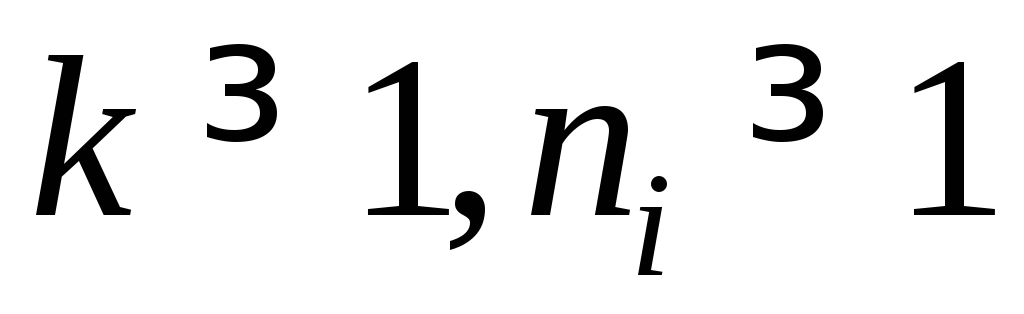 (5.18)
(5.18)
Два таких разложения числа 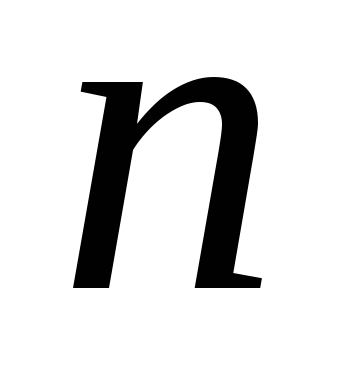 считаются разными, если они отличаются
хотя бы одним слагаемым. В таком случае
говорят о композиции числа
считаются разными, если они отличаются
хотя бы одним слагаемым. В таком случае
говорят о композиции числа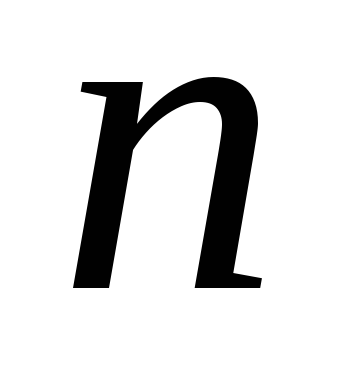 .
В ином случае,композиция числа
.
В ином случае,композиция числа 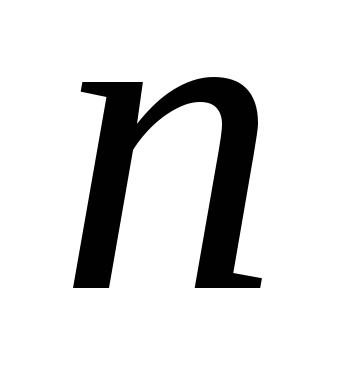 –это его разложение в виде (5.18), где
учитываются как величины слагаемых
(частей) , так и порядок их расположения
в сумме.
–это его разложение в виде (5.18), где
учитываются как величины слагаемых
(частей) , так и порядок их расположения
в сумме.
Пример. Выписать все композиции числа 3.
3=3, 3=2+1, 3=1+2, 3=1+1+1.
Композиции с ограничениями на количество слагаемых
Число композиций  числа
числа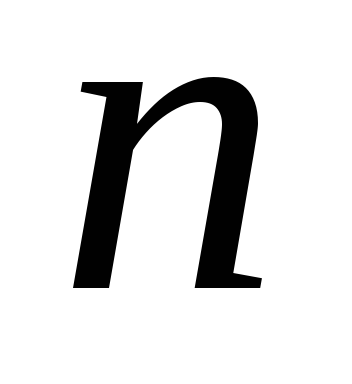 из
из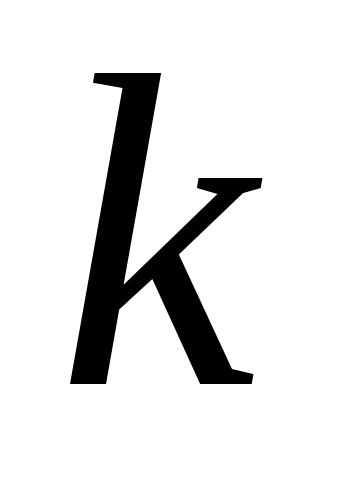 слагаемых равно числу распределений
слагаемых равно числу распределений одинаковых предметов по
одинаковых предметов по разным урнам при условии отсутствия
пустых урн. Число предметов, которые
попали в урну с номером
разным урнам при условии отсутствия
пустых урн. Число предметов, которые
попали в урну с номером
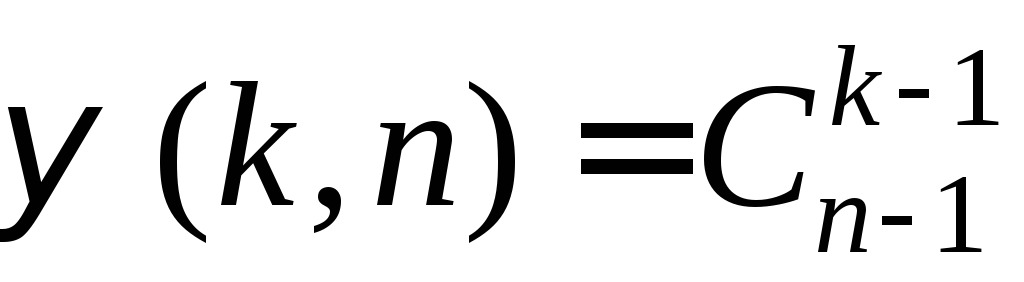 .
. Число всех композиций числа 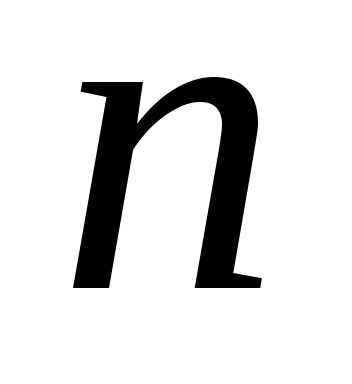
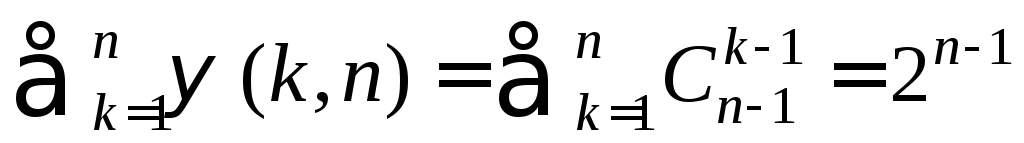 (5.19)
(5.19)
Комбинаторика разбиений
При анализе стратегий различных игр требуется подсчитывать количество комбинаций при раскладе определенных предметов. Наиболее распространенная карточная игра – преферанс. В классическом варианте этой игры карты раскладываются на 3 кучки (по числу играющих) и 2 карты кладутся в “прикуп“. Играют 32 картами, т. е. каждый игрок получает по 10 карт.
Определим количество вариантов расклада при игре в преферанс:
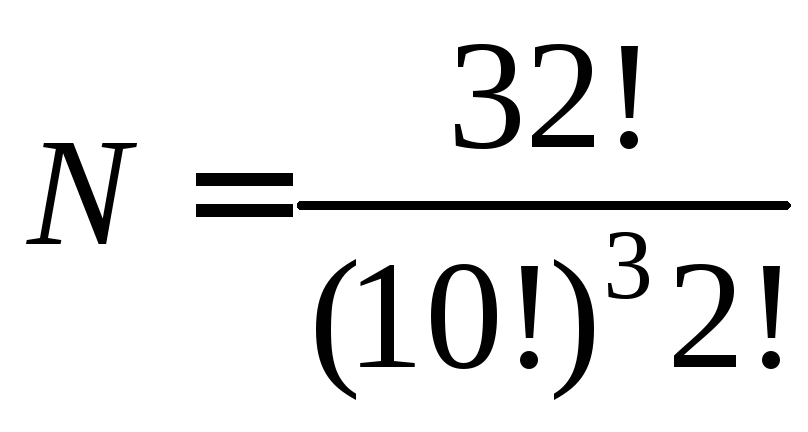
Для обоснования полученной формулы расставим все карты подряд и переставим их 32! способами. При каждой перестановке будем выделять первые 10 карт первому игроку, вторую десятку – второму, третью – третьему, а последние 2 карты будем откладывать в “прикуп”. После этого заметим, что перестановка 10 карт в руках каждого игрока не меняет варианта расклада, как и положения 2 карт в прикупе. Поэтому 32! разделим три раза на 10! и еще на 2!
В общем случае, если раскладываются  разных предметов по
разных предметов по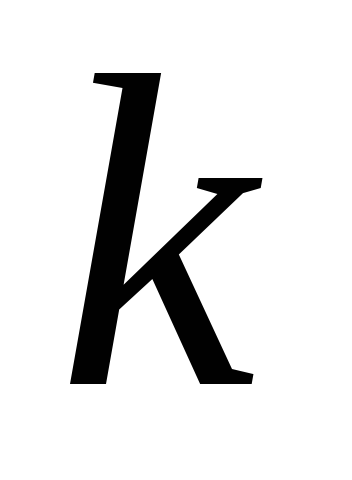 ящикам так, чтобы в 1-й ящик (кучку, игроку
в руки) попало
ящикам так, чтобы в 1-й ящик (кучку, игроку
в руки) попало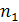 предметов, во второй предмета, в
предметов, во второй предмета, в
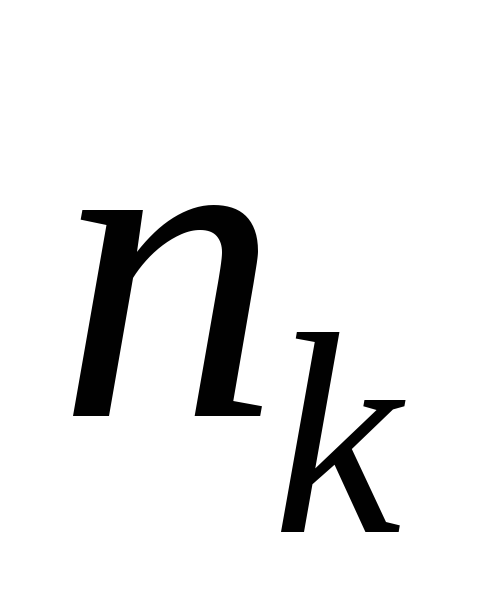 предметов, при этом
предметов, при этом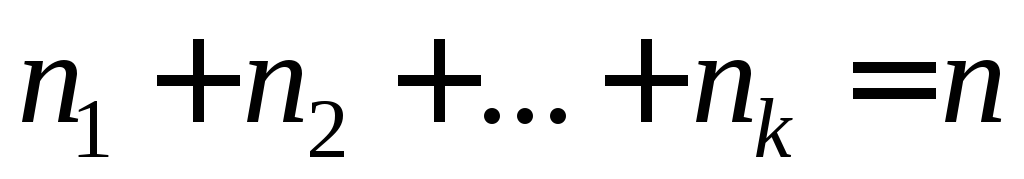 ,
то число вариантов расклада
,
то число вариантов расклада  (5.20)
(5.20)
Числа Белла — Википедия (с комментариями)
Материал из Википедии — свободной энциклопедии
В комбинаторике числом Белла <math>B_n</math> называется число всех неупорядоченных разбиений n-элементного множества, при этом по определению полагают <math>B_0 = 1</math>.
Численные значения
Значения чисел Белла <math>B_n</math> для <math>n=0,1,2,\dots</math> образуют последовательность:
- 1, 1, 2, 5, 15, 52, 203, 877, 4140, 21 147, 115 975 (последовательность A000110 в OEIS)
Явные формулы
Число Белла можно вычислить как сумму чисел Стирлинга второго рода:
- <math>B_n = \sum_{m=0}^n S(n,m)</math>
Для чисел Белла справедлива также формула Добинского:[1]
- <math>B_n = \frac{1}{e}\sum_{k=0}^\infty \frac{k^n}{k!}</math>.
Числа Белла можно задать в рекуррентном виде:
- <math>B_{n+1} = \sum_{k=0}^n \binom{n}{k} B_k</math>.
Свойства
Если <math>p</math> простое, то верно сравнение Тушара:
- <math>B_{n+p}\equiv B_n+B_{n+1}\pmod{p}</math>
и более общее:
- <math>B_{n+p^m}\equiv mB_n+B_{n+1} \pmod{p}.</math>
Производящая функция
Экспоненциальная производящая функция чисел Белла имеет вид[2]
- <math>\sum_{n=0}^\infty \frac{B_n}{n!} x^n = e^{e^x-1}</math>.
Напишите отзыв о статье «Числа Белла»
Примечания
Литература
- Яблонский С. В. Введение в дискретную математику. — М.: Высшая школа, 2006. — 392 с. — ISBN 5-06-005683-X.
Отрывок, характеризующий Числа Белла
– В Москве? – сказал он вопросительно. – Да, в Москве. Прощайте.– Ах, желала бы я быть мужчиной, я бы непременно осталась с вами. Ах, как это хорошо! – сказала Наташа. – Мама, позвольте, я останусь. – Пьер рассеянно посмотрел на Наташу и что то хотел сказать, но графиня перебила его:
– Вы были на сражении, мы слышали?
– Да, я был, – отвечал Пьер. – Завтра будет опять сражение… – начал было он, но Наташа перебила его:
– Да что же с вами, граф? Вы на себя не похожи…
– Ах, не спрашивайте, не спрашивайте меня, я ничего сам не знаю. Завтра… Да нет! Прощайте, прощайте, – проговорил он, – ужасное время! – И, отстав от кареты, он отошел на тротуар.
Наташа долго еще высовывалась из окна, сияя на него ласковой и немного насмешливой, радостной улыбкой.
Пьер, со времени исчезновения своего из дома, ужа второй день жил на пустой квартире покойного Баздеева. Вот как это случилось.
Проснувшись на другой день после своего возвращения в Москву и свидания с графом Растопчиным, Пьер долго не мог понять того, где он находился и чего от него хотели. Когда ему, между именами прочих лиц, дожидавшихся его в приемной, доложили, что его дожидается еще француз, привезший письмо от графини Елены Васильевны, на него нашло вдруг то чувство спутанности и безнадежности, которому он способен был поддаваться. Ему вдруг представилось, что все теперь кончено, все смешалось, все разрушилось, что нет ни правого, ни виноватого, что впереди ничего не будет и что выхода из этого положения нет никакого. Он, неестественно улыбаясь и что то бормоча, то садился на диван в беспомощной позе, то вставал, подходил к двери и заглядывал в щелку в приемную, то, махая руками, возвращался назад я брался за книгу. Дворецкий в другой раз пришел доложить Пьеру, что француз, привезший от графини письмо, очень желает видеть его хоть на минутку и что приходили от вдовы И. А. Баздеева просить принять книги, так как сама г жа Баздеева уехала в деревню.
Высокототиентное число — Википедия
Материал из Википедии — свободной энциклопедии
Высокототиентное число — это целое число k, имеющее больше решений уравнения
- x − φ(x) = k,
чем для любого другого числа, меньшего k. Здесь φ — функция Эйлера, значение функции называется тотиентом. Несколько первых высокототиентных чисел: 1, 2, 4, 8, 12, 24, 48, 72, 144, 240, 432, 480, 576, 720, 1152, 1440 (последовательность A097942 в OEIS), с 1, 3, 4, 5, 6, 10, 11, 17, 21, 31, 34, 37, 38, 49, 54 и 72 решениями соответственно. Последовательность высокототиентных чисел является подмножеством наименьших чисел k с точно n решениями уравнения φ(x) = k [1]
Тотиентом числа x, с разложением x=∏ipiei{\displaystyle x=\prod _{i}p_{i}^{e_{i}}}, является произведение:
- ϕ(x)=∏i(pi−1)piei−1.{\displaystyle \phi (x)=\prod _{i}(p_{i}-1)p_{i}^{e_{i}-1}.}
Таким образом, высокототиентное число — это число, которое имеет больше путей представления в виде произведения этого вида, чем любое меньшее число.
Концепция чем-то аналогична концепции высокосоставных чисел[en]. Число 1 является единственным нечётным высокоставным числом, и точно так же 1 является единственным нечётным высокототиентным числом (на самом деле, все нечётные числа нетотиентны). И так же, как существует бесконечно много высокосоставных чисел, существует бесконечно много высокототиентных чисел, хотя найти высокототиентные числа труднее, чем найти высокосоставные, поскольку требует факторизации на простые множители, что становится крайне сложно по мере роста чисел.
| По формуле | |
|---|---|
| Последовательности | |
| По свойствам | |
| Зависящие от системы счисления | |
| Модели | Близнецы (p, p + 2) • Цепочка близнецов (n ? 1, n + 1, 2n ? 1, 2n + 1, …) • Тройка простых (p, p + 2 или p + 4, p + 6) • Четвёрка простых (p, p + 2, p + 6, p + 8) • k?Кортеж • Родственные (p, p + 4) • Отличающиеся на 6 (p, p + 6) • Чена • Софи Жермен (p, 2p + 1) • Цепи Куннингама (p, 2p ± 1, …) • Безопасные (p, (p ? 1)/2) • Прогрессии (p + a•n, n = 0, 1, …) • Сбалансированные (последовательные p ? n, p, p + n) |
| По размеру | |
| Комплексные числа | |
| Составные числа | |
| Связанные разделы | |
1 — один. натуральное нечетное число. число фибоначчи f1 и f2, число белла b0 и b1, число каталана c0 и c1, факториал 0! и 1!, регулярное число (число хемминга). в ряду натуральных чисел находится между числами 0 и 2. Все о числе один.
- Главная
- О числе 1
1 — один. Натуральное нечетное число. Число Фибоначчи F1 и F2, Число Белла B0 и B1, Число Каталана C0 и C1, Факториал 0! и 1!, Регулярное число (Число Хемминга). В ряду натуральных чисел находится между числами 0 и 2.
Like если 1 твое любимое число!
Распространенные значения и факты
01 регион — Республика Адыгея
- Столица
- Майкоп
- Автомобильный код
- 01
- Федеральный округ
- Южный
- Экономический район
- Северо-Кавказский
- Дата образования
- 27 июля 1922 г.
- Территория
- 7,6 тыс. кв. км. 0,04 % от РФ 86 место в РФ
- Население
- Общая численность 477 тыс. чел.
Изображения числа 1
Склонение числа «1» по падежам
| Падеж | Вспомогательное слово | Характеризующий вопрос | Склонение числа 1 |
|---|---|---|---|
| Именительный | Есть | Кто? Что? | один |
| Родительный | Нет | Кого? Чего? | одного |
| Дательный | Дать | Кому? Чему? | одному |
| Винительный | Видеть | Кого? Что? | один |
| Творительный | Доволен | Кем? Чем? | одним |
| Предложный | Думать | О ком? О чём? | одном |
Перевод «один» на другие языки
- Азербайджанский
- bir
- Албанский
- një
- Английский
- one
- Арабский
- واحد
- Армянский
- մեկ
- Белорусский
- адзін
- Болгарский
- един
- Вьетнамский
- một
- Голландский
- een
- Греческий
- ένας
- Грузинский
- ერთი
- Иврит
- אחד
- Идиш
- מען
- Ирландский
- amháin
- Исландский
- einn
- Испанский
- uno
- Итальянский
- uno
- Китайский
- 一
- Корейский
- 한
- Латынь
- unum
- Латышский
- viens
- Литовский
- vienas
- Монгольский
- нэг
- Немецкий
- ein
- Норвежский
- ett
- Персидский
- یک
- Польский
- jeden
- Португальский
- um
- Румынский
- unul
- Сербский
- један
- Словацкий
- jeden
- Словенский
- ena
- Тайский
- หนึ่ง
- Турецкий
- bir
- Украинский
- один
- Финский
- yksi
- Французский
- un
- Хорватский
- jedan
- Чешский
- jeden
- Шведский
- ett
- Эсперанто
- unu
- Эстонский
- üks
- Японский
- 1
Перевод «1» на другие языки и системы
Римскими цифрами
- Римскими цифрами
- I
Сервис перевода арабских чисел в римские
Арабско-индийскими цифрами
- Арабскими цифрами
- ١
- Восточно-арабскими цифрами
- ۱
- Деванагари
- १
- Бенгальскими цифрами
- ১
- Гурмукхи
- ੧
- Гуджарати
- ૧
- Ория
- ୧
- Тамильскими цифрами
- ௧
- Телугу
- ౧
- Каннада
- ೧
- Малаялам
- ൧
- Тайскими цифрами
- ๑
- Лаосскими цифрами
- ໑
- Тибетскими цифрами
- ༡
- Бирманскими цифрами
- ၁
- Кхемерскими цифрами
- ១
- Монгольскими цифрами
- ᠑
В других системах счисления
- 1 в двоичной системе
- 1
- 1 в троичной системе
- 1
- 1 в восьмеричной системе
- 1
- 1 в десятичной системе
- 1
- 1 в двенадцатеричной системе
- 1
- 1 в тринадцатеричной системе
- 1
- 1 в шестнадцатеричной системе
- 1
QR-код, MD5, SHA-1 числа 1
Адрес для вставки QR-кода числа 1, размер 500×500:http://pro-chislo.ru/data/moduleImages/QRCodes/1/68f84c0088bf54ba3bfd853ec2c1270a.png
- MD2 от 1
- c92c0babdc764d8674bcea14a55d867d
- MD4 от 1
- 8be1ec697b14ad3a53b371436120641d
- MD5 от 1
- c4ca4238a0b923820dcc509a6f75849b
- SHA1 от 1
- 356a192b7913b04c54574d18c28d46e6395428ab
- SHA256 от 1
- 6b86b273ff34fce19d6b804eff5a3f5747ada4eaa22f1d49c01e52ddb7875b4b
- SHA384 от 1
- 47f05d367b0c32e438fb63e6cf4a5f35c2aa2f90dc7543f8a41a0f95ce8a40a313ab5cf36134a2068c4c969cb50db776
- SHA512 от 1
- 4dff4ea340f0a823f15d3f4f01ab62eae0e5da579ccb851f8db9dfe84c58b2b37b89903a740e1ee172da793a6e79d560e5f7f9bd058a12a280433ed6fa46510a
- GOST от 1
- b0f784fe99f37c57188d100f79bffa0e877f38c8ad50baf7e474b7596a02b5bf
- Base64 от 1
- MQ==
1й день в году
1й день в не високосном году — 1 января
Новый год
Новый год — праздник, отмечаемый многими народами в соответствии с принятым календарём, наступающий в момент перехода с последнего дня года в первый день следующего года. Обычай праздновать Новый год существовал уже в Месопотамии в третьем тысячелетии до нашей эры. Начало года с 1 января было установлено римским правителем Юлием Цезарем в 46 году до н. э. В Древнем Риме этот день был посвящён Янусу — богу выбора, дверей и всех начал. Месяц январь получил своё название в честь бога Януса, которого изображали с двумя лицами: одно смотрело вперёд, а другое — назад.
Всемирный день мира
«Всемирный день мира» (англ. World Day of Peace) или «День всемирных молитв о мире» — международный праздник, во время которого верующие призывают Бога прекратить все войны и ниспослать людям мир на Земле. Отмечается каждый год, 1 января.
День памяти былинного богатыря Ильи Муромца
Рождественский пост
Рожде́ственский пост (Фили́ппов пост, в просторечии Фили́пповки) — христианский пост, установленный в честь Рождества Христова. Соблюдается с 15 (28) ноября по 24 декабря (6 января).
1й день в високосном году — 1 января
Математические свойства числа 1
- Простые множители
- 1
- Делители
- 1
- Количество делителей
- 1
- Сумма делителей
- 1
- Простое число
- Нет
- 1е простое число
- 2
- Число Фибоначчи
- Да F1 и F2
- Число Белла
- Да B0 и B1
- Число Каталана
- Да C0 и C1
- Факториал
- Да 0! и 1!
- Регулярное число (Число Хемминга)
- Да
- Совершенное число
- Нет
- Квадрат
- 1
- Квадратный корень
- 1
- Натуральный логарифм (ln)
- 0
- Десятичный логарифм (lg)
- 0
- Синус (sin)
- 0.8414709848079
- Косинус (cos)
- 0.54030230586814
- Тангенс (tg)
- 1.5574077246549
Фильмы про 1
1 минуту (1 a Minute), 2010 год
Фильм «1 минуту» — это документальная драма основана на событиях жизней людей,а также жизни самого режиссера, который борется с раком.…
1+1 (Intouchables), 2011 год
Аристократ Филипп, ставший инвалидом после несчастного случая, берет себе в помощники молодого мужчину, коего даже с натяжкой нельзя назвать подходящим…
1, 2, 3, Белая мгла (1, 2, 3, Whiteout), 2007 год
Фильм «1, 2, 3, Белая мгла» — это фантастическая драма, которая больше похожа на аудио-визуальных эксперимент, чем на полноправное кино.…
Все фильмы о числе 1 (4)