Числа Белла
|
|
|
|||||||||||||||||||||||||||
Частное решение.
Угол между ними.
Матрица смежности онлайнСиндром ломкой Х хромосомы: определение числа CGG повторов (синдром Мартина-Белла)
Срок: 20р.
Материал: венозная кровь с EDTA 4 мл
Стоимость: 8900 грн
Заказать
Хотите получить скидку? Сделайте видео- или фотоотзыв! Подробнее об акциях
При сдаче теста в городах кроме Киева — доплата 500 грн к заказу и срок + 3 дня.
Синдром ломкой Х-хромосомы (синдром Мартина-Белла) является генетическим заболеванием, которое вызывает умственную отсталость, расстройства в поведении и обучении, влияет на физические характеристики пациента. Хотя синдром ломкой Х-хромосомы может встречаться у лиц обоего пола, мужчины страдают этим заболеванием чаще, чем женщины и протекает оно у мужчин более тяжело. center>
Причина заболевания кроется в особом строении Х-хромосомы. Его генетическая основа — это увеличение числа тринуклеотидных повторов (CGG) в длинном плече Х-хромосомы. У здоровых людей число этих повторов составляет от 6 до 54.
У женщин чаще встречается премутация, то есть количество CGG-повторов составляет 55-200. Умственная отсталость и клиника заболевания в этом случае не развивается, однако женщины-носительницы премутации страдают преждевременным истощением яичников, а также бесплодием, либо невынашиванием беременности.
Частота рождения ребенка с данной патологией в нашей популяции составляет от 1:2000 до 1:4000.
В случае установления бессимптомного носительства мутации у женщины может быть рекомендовано использование донорских ооцитов или проведение предимплантационной генетической диагностики с целью селекции эмбриона женского пола.
Унаследовав нормальный аллель от отца, девочка не будет страдать данным заболеванием, хотя и может быть носителем одной патологической Х-хромосомы.
Метод исследования основан на полимеразной цепной реакции с детекцией количества повторов на капиллярном электрофорезе.
Проводится забор венозной крови в вакуумную пробирку с EDTA К2 или К3 (фиолетовая/сиреневая крышка) 4 мл.
Требования сдачи крови натощак нет (легкий завтрак и незадолго до взятия крови выпить 1-2 стакана обычной негазированной воды; детей обязательно поить негазированной водой порциями, до 150-200 мл, в течение 30 минут), в день сдачи крови не употреблять медикаменты (включая витамины и БАД), накануне исключить прием жареной и жирной пищи.
Рекомендовано предоставить выписку/заключение врача, заполнить бланк заказа.
Во всех случаях по результатам необходимо получить консультацию врача-генетика.
Ваш голос учтен!
4.
9
/
5.0
(2 голосов)
Вычисление чисел Белла
fredrikj.net / blog /
6 августа 2015 г.
Числа Белла $B_n$ подсчитывают количество способов множество из $n$ элементов можно разбить на непересекающиеся подмножества. целочисленная последовательность $B_0, B_1, \ldots$ (OEIS A000110) начинается с $$1, 1, 2, 5, 15, 52, 203, 877, 4140, 21147, \ldots$$
Легко видеть, что $B_n \le n!$ по индукции. Разбиение множества $A = \{a_1, \ldots, a_{n-1}\}$ можно продолжить до разбиения множества $A \cup \{a_n\}$ не более чем на $n$ различных способами: мы можем либо добавить $a_n$ к одному из существующих подмножеств (которых не более $n-1$), либо создать новое подмножество, содержащее только $a_n$.
Действительно, числа Белла растут почти так же быстро, как эта верхняя граница, размер которой составляет $\log n! = n \log n — n + O(\log n)$ по формуле Стирлинга.
{W(x)} = x$.
9{2+o(1)}$, т.е.
квазиквадратичны по размеру результата.
Точное вычисление чисел Белла
Самый простой способ вычислить числа Белла — это использовать числовой треугольник напоминающий треугольник Паскаля для биномиальных коэффициентов. Числа Белла появляются на краях треугольника. Начиная с 1, каждая новая строка в треугольнике строится путем взятия последней записи в предыдущей строке как первая запись, а затем установка каждого новая запись для своего левого соседа плюс его верхний левый сосед: 9{1+o(1)}$ раз. Сочетание EGF с многомодульной оценкой для вычисления целые числа $B_0, \ldots, B_n$ одновременно весьма привлекательны поскольку он избегает знаменателей факторного размера, которые мы получаем, когда выполнение арифметических действий в $Q[[x]]$.
Я реализовал большинство описанных алгоритмов выше во FLINT еще в 2011 году.
- bell_number_bsplit.c вычисляет изолированное число Белла, используя формулу Добински и двоичное разбиение
- bell_number_multi_mod.
c
вычисляет изолированное число Белла, используя конечную формулу Добински и многомодульное вычисление - bell_number_vec_recursive.c вычисляет вектор чисел Белла, используя алгоритм рекурсивного числового треугольника
- bell_number_vec_multi_mod.c вычисляет вектор чисел Белла, используя многомодульную оценку (на основе EGF по модулю малых простых чисел)
- bell_number_nmod.c вычисляет изолированное число Белла по модулю $p$, используя конечную формулу Добински
- bell_number_nmod_vec_recursive.c вычисляет вектор чисел Белла по модулю $p$, используя алгоритм рекурсивного числового треугольника
- bell_number_nmod_vec_series.c вычисляет вектор чисел Белла по модулю $p$, используя EGF
c
вычисляет изолированное число Белла, используя конечную формулу Добински и многомодульное вычислениеЕсть также по умолчанию функции FLINT, которые автоматически выбирают (примерно, в зависимости от железа) самый быстрый алгоритм.
В следующей таблице показано, сколько секунд занимает FLINT с соответствующим алгоритмом на моем ноутбуке:
| нет | vec_recursive | vec_multi_mod | bsplit | мульти_мод |
| 10 | 0. 000000013* | 0.0000076 | 0.0000039 | 0.0000059 |
| 100 | 0.00011 | 0.00033 | 0.000031 | 0.000094 |
| 1000 | 0.070 | 0.30 | 0.0060 | 0,0093 |
| 10000 | 87 | 118 | 3,1 | 1,2 |
| 100000 | — | — | 858 | 164 |
Обратите внимание, что тайминги для первых двух алгоритмов предназначены для одновременного вычисления первых $n$ чисел Белла, а последние два предназначены для вычисления только $B_n$. Звездочка (*) означает, что код на самом деле обманывает здесь, используя таблицу поиска, когда $n
Мы видим, что алгоритм числового треугольника
превосходит EGF (vec_multi_mod) при разумных значениях $n$.
Алгоритм числового треугольника имеет худшую асимптотическую сложность, но намного
ниже накладные расходы.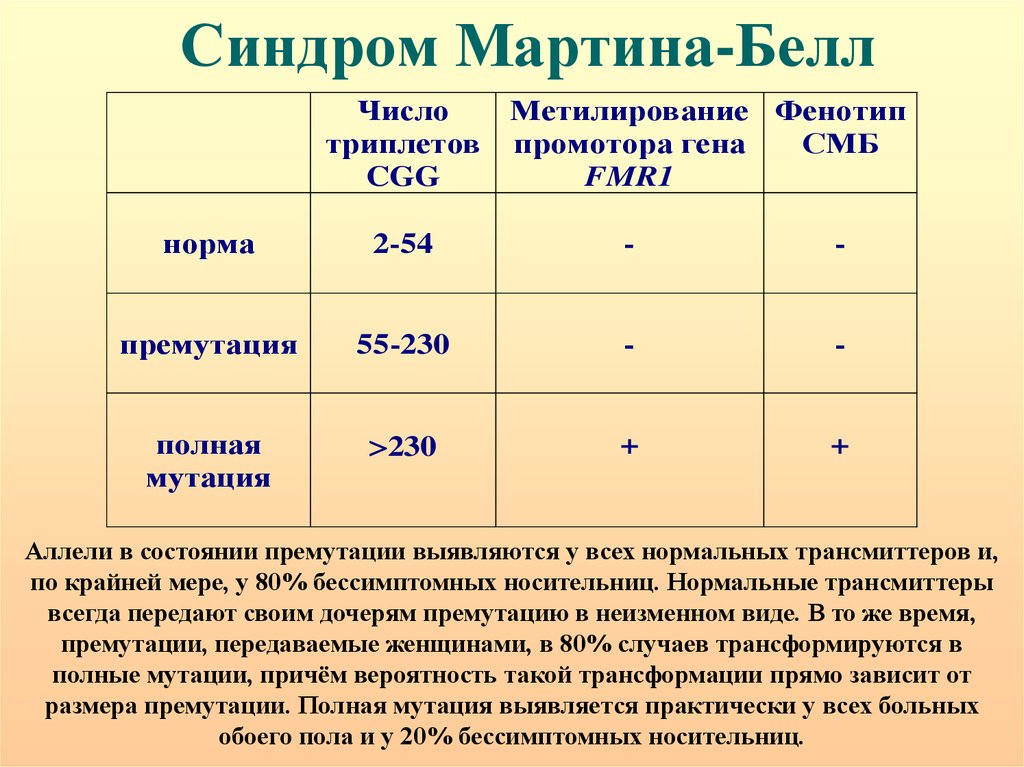
Я не реализовал распараллеливание алгоритмов multi_mod. Это должно дать почти двукратное ускорение на моем двухъядерном процессоре.
Во FLINT нет реализации на основе OGF, но я тестировал этот алгоритм, и у него почти одинаковая скорость к EGF с многомодульной оценкой.
Приблизительный расчет числа звонков
Теперь предположим, что вместо вычисления точного значения $B_n$ мы довольны старшими цифрами $d$, где $d$ для Например, может быть 10, 100 или 1000. Ясно, что если мы рассмотрим 9{(N+1)}(m), \ldots$ и, в свою очередь, остаток ряда Тейлора.
Пусть
$$T(z) = \exp(F(z)), \quad F(z) = n \log(z) — \log \Gamma(z+1).$$
Ясно, что $|T(z)| \le \exp(|F(z)|)$.
У нас есть
$$
\sup_{|z-m|\le R} |F(z)| \le |F(m)| + R \sup_{|z-m|\le R} |F'(z)|.
$$
Однако, непосредственно ограничивая
$$
F'(z) = \frac{n}{z} — \psi(z+1)
$$
не работает, так как есть
является катастрофическим сокращением ($F'(z) \ приблизительно 0$ имеет место по построению, когда $z \ приблизительно m$).
{2+o(1)}$ точном вычислении $B_n$
(при условии, что все, что нам нужно, это числовое приближение)!
9k$, чтобы гарантировать точность результата до $d$ цифр, несмотря на ошибки округления.
Я не вижу простого способа подобрать все эти параметры оптимально априори , так как они сложным образом зависят друг от друга. Рабочая точность особенно трудно выбрать, так как это зависит от деталей, лежащих в основе алгоритмы для гамма-функции, для умножения степенных рядов, и так далее. Мое решение состояло в том, чтобы всегда выбирать отношение $r / R = 1/8$ (что дает три бита на член) и выбрав как количество подразделений и рабочая точность адаптивно: 92$$ где $p$ — точность в битах. Например:
- Чтобы вычислить 10-значное приближение $B_n$, ряд Тейлора работает быстрее, если $n$ больше 5 миллионов.
- Чтобы вычислить 100-значное приближение $B_n$, ряд Тейлора работает быстрее, если $n$ больше 500 миллионов.
- Чтобы вычислить 1000-значное приближение $B_n$, ряд Тейлора работает быстрее, если $n$ больше 50 миллиардов.
На следующем графике показано время, за которое arb_bell_fmpz для вычисления цифр от $B_n$ до $d$, где $d$ равно 10, 100, 1000 и $\infty$ (точное вычисление $B_n$). 9{100}}$, количество разделов набора с 1 элементом гугола, с точностью до 1000 цифр:
522814709141082608913334784314134261851806
2232888949657946267157517765591827437575568527323435768792618847167888789438948060302478614199779726
3678257759505994042279245062445753647863874788822306413960438998857329199453620537788749942016823439
68267785858225339422083619687423225479298171524242007012081418958404496161123201363892701142452
0592967211088076726689116500153640131057718252616451791806734296741516356176155638789662447036908840
738627453
02672752037690916240689650852398468230120896448383085739867131963399875467499177815304267568743
4662852459854922316072421122078373333676860456717485594671823500441075731431468000467316898340014880
05634995376054080240205182329713875701872552257243678139133679365822937731151484061913797597293
70242425082172677880169805458277444328503091835330854941844204279433189349120410802200732718571
· 10 972157574857696235378663027434211359218006858504930450816134076178889687987618389929416815288755835629
± 4.
{n+1/2} \exp\left(n/W(n) — n — 1\вправо)$
предлагает значение 9{O(1)} n$ работают с фиксированной точностью).
Сомневаюсь, что этот код можно использовать в реальной жизни, но было весело. упражнение делать. Меня не очень интересуют числа Белла как таковые, а скорее в алгоритмах. Как обычно, взгляд на конкретную проблему помогает понять инструменты, доступные для решения более сложных проблем. В этом случае используются несколько функций Arb:
- Поддержка простой работы с аппроксимациями вещественных чисел с переменной точностью и автоматическим отслеживанием границ их ошибок. 9k$$, который реализован в mpmath.
Задача читателю: можете ли вы придумать более быстрый способ вычисления чисел Белла (приблизительно или точно)? Насколько точно вы можете аппроксимировать $B_n$, используя асимптотические разложения, если вы использовать поправочные члены высокого порядка? Можете ли вы сделать это с помощью эффективных и строгих ограничений погрешности?
fredrikj.
net |
Индекс блога |
RSS-канал |
Подписывайтесь на меня на Mastodon |
Стать спонсоромко.комбинаторика — На колокольчиках
$\begingroup$
Изменить (первая версия была сформулирована неверно. Спасибо Дугласу и другим за ваши исправления) Пусть $B_n$ будет $n$-м номером Белла (количество разделов множества с $n$ элементами). Для каждого $n > 3$ у меня есть набор $A_n$ размера $|A_n|=B_n$. Затем у меня есть подмножество $A’_n \subset A_n$, где $|A’_n|=B_n-B_{n-1}$. Я хотел бы сказать кое-что о размере $A’_n$ относительно размера $A_n$. Например, кажется, что $lim_{n \to \infty} \frac{B_{n-1}}{B_n}=0$. Могу ли я сделать более сильное утверждение об отношении последовательных чисел Белла? Как я могу формализовать утверждение «для достаточно больших $n$ большая часть $A_n$ находится в $A’_n$».
- кокомбинаторика
$\endgroup$
2
$\begingroup$
Легко видеть, что $B_n \ge 2 B_{n-1}$, поскольку у нас всегда есть выбор: добавлять $n$ к той же части, что и $n-1$, или нет.
net |
Индекс блога |
RSS-канал |
Подписывайтесь на меня на Mastodon |
Стать спонсором
