Числа Белла
Число Белла равно количеству разбиений множества из элементов на произвольное количество непустых подмножеств, которые не пересекаются. Очевидно, что, так как существует только одно разбиение пустого множества. Например,, так как существует 5 возможных разбиений множестваиз трех элементов:
Заметим, что элементов можно разбить намножеств. При этом количество разбиений– элементного множества наподмножеств равно числу Стирлинга 2 рода. Откуда получаем формулу:
0 | 1 | 2 | 3 | 4 | 5 | 7 | 8 | 9 | 10 | ||
1 | 1 | 2 | 5 | 15 | 52 | 203 | 877 | 4140 | 21147 | 115975 |
Рассмотрим следующие
конструкции, в которых точки обозначают
одноэлементные множества, а сегменты
объединяют элементы, принадлежащие
одному множеству.
Из
элементов можно построитьразных таких конструкций.
Теорема. Числа Белла удовлетворяют следующему рекуррентному соотношению:
Доказательство. Рассмотрим разбиение элемента в зависимости от величины блока, в котором находится– ый элемнент. Пусть размер этого блока равен. Тогда существуетспособов выбрать в него кроме– ого ешеэлемент. Остальныеэлементов можно разбитьспособами.Таким образом:
Пример.Например, . Числа Белла удовлетворяют следующему свойству:
Для значений получим следующие значения детерминанта:
1, 1, 2, 12, 288, 34560, 24883200, 125411328000, 5056584744960000, 1834933472251084800000, 6658606584104736522240000000, …
При разложении функции в ряд Маклорена коэффициенты ряда образуют числа Белла:
Числа
могут быть построены при помощитреугольника Белла.
Композиции
При решении задач про распределениеодинаковых предметов междунепустыми урнами можно говорить о разложении числав сумму натуральных слагаемых:
, где(5.18)
Два таких разложения числа считаются разными, если они отличаются хотя бы одним слагаемым. В таком случае говорят о композиции числа. В ином случае,композиция числа –это его разложение в виде (5.18), где учитываются как величины слагаемых (частей) , так и порядок их расположения в сумме.
Пример. Выписать все композиции числа 3.
3=3, 3=2+1, 3=1+2, 3=1+1+1.
Композиции с ограничениями на количество слагаемых
Число композиций
числаизслагаемых равно числу распределенийодинаковых предметов поразным урнам при условии отсутствия
пустых урн.
Число предметов, которые
попали в урну с номером,
дает слагаемое . Отсюда выплывает, что.
Число всех композиций числа
(5.19)
Комбинаторика разбиений
При анализе стратегий различных игр требуется подсчитывать количество комбинаций при раскладе определенных предметов. Наиболее распространенная карточная игра – преферанс. В классическом варианте этой игры карты раскладываются на 3 кучки (по числу играющих) и 2 карты кладутся в “прикуп“. Играют 32 картами, т. е. каждый игрок получает по 10 карт.
Определим количество вариантов расклада при игре в преферанс:
Для обоснования полученной формулы
расставим все карты подряд и переставим
их 32! способами. При каждой перестановке
будем выделять первые 10 карт первому
игроку, вторую десятку – второму, третью
– третьему, а последние 2 карты будем
откладывать в “прикуп”. После этого
заметим, что перестановка 10 карт в руках
каждого игрока не меняет варианта
расклада, как и положения 2 карт в прикупе.
Поэтому 32! разделим три раза на 10! и еще
на 2!
В общем случае, если раскладываются разных предметов поящикам так, чтобы в 1-й ящик (кучку, игроку в руки) попалопредметов, во второй предмета, в-й –предметов, при этом, то число вариантов расклада
(5.20)
Число Белла
множества B A , содержащего элемент n, существует в точности
S(n-b,k-1) разбиений множества А на k блоков, содержащих B в качестве блока. Действительно, каждое такое разбиение однозначно соответствует разбиению множества А\В на k-1 блоков. b- элементное множество B A , содержащее элемент n, можно выбрать С(n-1,b-1) способами. Следовательно
S(n, k)
n−(k −1)
= ∑
b=1
n−(k −1)
= ∑ Cb−−1S(n −b, k −1) =
n 1
b=1
n−1
Cn−−b S(n −b, k −1) = ∑Ci − S(i, k −1).
n 1 n 1 i=k −1
Определение. Число Белла Bn есть число всех разбиений n- элементного множества Bn = Π (A) , где A = n.
Другими словами
n
Bn = ∑
k =0
Теорема
S(n, k).
n
3.3. B + = ∑Ci B .
n 1 n i i=0
Доказательство.
Множество всех разбиений множества A={1,…,n+1} можно разбить на различные классы в зависимости от блока В, содержа-
щего элемент n+1 | (или в зависимости от множества А\В). Для каж- | ||||||||
дого множества | A \ B {1,…, n} существует в точности | ||||||||
|
| Π ( A \ B) |
| = B |
| A−B |
|
| разбиений множества А, содержащих В в каче- |
|
| ||||||||
|
|
|
|
| |||||
|
|
|
|
|
|
|
|
|
|
стве блока.
Группируя классы в зависимости от мощности множества А\В, получаем требуемую формулу.
B(0)=1
B(1)=1
B(2)=2
B(3)=5
B(4)=15
B(5)=52
B(6)=203
Таблица 3.2. Числа Белла.
12
Числа Стирлинга первого рода
Введем следующее обозначение многочлена
[x]k | = x(x −1)…(x −k +1) |
| |
Для частных случаев: |
| ||
[x]0 | =1, | . | |
[x]1 =1, | |||
| |||
[x]2 | = x(x −1), |
| |
[x]3 | = x(x −1)(x −2). |
| |
Определение. Числа Стирлинга первого рода s(n,k) есть коэффициенты при последовательных степенях переменной x в много-
члене [x]k :
n |
|
[x]n = ∑s(n, k)xk . |
|
k =0 |
|
Очевидно, что s(n,k)=0 для k>n. |
|
Теорема 3.4. |
|
s(n, k) = s(n −1, k −1) −(n −1)s(n −1, k) , для 0 < k < n, | (3.4) |
s(n, n) =1 , для n ≥ 0, | (3.5) |
s(n,0) = 0 , для n >0. | (3.6) |
Доказательство.
Формулы (3.5) и (3.6) очевидны. Формулу (3.4) получим, сравнивая коэффициенты при xk в обеих частях равенства
[x]n =[x]n−1 (x −n +1).
Имеем
n |
| n−1 |
|
|
|
|
|
| |
∑s(n, k)xk = (x −n =1)∑s(n −1, k)xk = |
|
| |||||||
k =0 |
| k =0 |
|
|
|
|
|
| |
n−1 |
|
| n−1 |
|
|
| |||
= ∑s(n −1, k)xk +1 −(n −1)∑s(n, k)xk = |
|
| |||||||
k =0 |
|
| k =0 |
|
|
| |||
n−1 |
|
|
|
|
|
|
|
| |
∑(s(n −1, k −1) −(n −1)s(n −1, k))xk + |
|
| |||||||
k =1 |
|
|
|
|
|
|
|
| |
+ s(n −1, n −1)xn −(n −1)s(n −1,0). |
|
|
| ||||||
| k | 0 | 1 |
| 2 |
| 3 | 4 | 5 |
|
|
|
|
|
|
|
|
|
|
13
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 | 1 | 0 | 0 | 0 | 0 | 0 |
1 | 0 | 1 | 0 | 0 | 0 | 0 |
2 | 0 | -1 | 1 | 0 | 0 | 0 |
3 | 0 | 2 | -3 | 1 | 0 | 0 |
4 | 0 | -6 | 11 | -6 | 1 | 0 |
5 | 0 | 24 | 50 | 35 | -10 | 1 |
Таблица 3.
3. Числа Стирлинга первого рода.
Лекция 4. Формулы включений и исключений.
Формулы включений и исключений
Лемма 4.1. Пусть дано N элементов и n свойств p1,…,pn. Пусть Ni1 …ir — число элементов, обладающих, по крайней мере, свойст-
вами pi1 ,… pir ,r =1,n . Тогда число элементов N0 , не обладающих ни одним из указанных свойств определяется формулой
n |
| ∑Ni1 …is |
|
N0 = N −∑Ni + ∑Ni1i2 +… +(−1)s | +… | ||
i=1 | i1 <i2 | i1 <i2 <…<is | (4.1) |
+(−1)n N12…n
Доказательство. Рассмотрим правую часть (4.1). Элемент, не обладающий свойствами p1,…,pn, учитывается только в слагаемом N. Любой элемент A, обладающий ровно r свойствами j1,…,jr учитывается в выражении
∑Ni1…is , s ≤ r, Crs раз.
i1<i2 <…<is
Следовательно, вклад A в правую часть (4.1) равен:
1−Cr1 +Cr2 +… +(−1)s Crs +… +(−1)r Crr = (1−1)r = 0r = 0 .
Пример 4.1. (пояснение к предыдущей формуле)
Рассмотрим множество шаров, которые могут быть окрашены в 4 цвета:
желтый – свойство 1; красный – свойство 2; синий – свойство 3; зеленый – свойство 4.
Пусть некоторый шар окрашен одновременно в желтый, красный и зеленый цвета. Тогда для него N0 = 0. Теперь рассмотрим,
14
какой вклад он дает в правую часть равенства (4.1).
В первом слагаемом он учитывается 1 раз. Во втором слагаемом он учитывается C31 =3 раза (т.к. N1 = 1, N2 = 1, N4 = 1). В
третьем слагаемом он учитывается C32 =3 раза (т.к. N12 = 1, N14 = 1, N24 = 1). В четвертом слагаемом он учитывается C33 =1 раз (т.к.
N124=1). В пятом (последнем для рассматриваемого примера) сла-
гаемом он учитывается 0 раз (т.к. N1234 = 0).
Таким образом, вклад рассматриваемого шара в правую часть равенства (4.
1) равен 1 – 3 + 3 – 1 + 0 = 0.
Замечание. Формула (4.1) называется формулой включений и исключений.
Пример 4.2. (задача о беспорядках).
Определить количество перестановок a1,…,an, чисел 1,…,n та-
ких, что ai ≠ i,i =1,n .
Решение. Число всех перестановок N=n!
Свойство si : ai = i,i = 1, n .
Ni1 ,…,ir — число перестановок, оставляющих на месте по крайней мере числа i1,…,ir , следовательно, Ni1 ,…,ir = (n − r)!
В ∑Ni1 ,…,ir имеется Cnr слагаемых – количество способов
i1 <…<ir
выбора чисел i1,…,ir из 1,…,n. Итак, на основании (4.1):
N0 = n!−Cn1 (n −1)!+Cn2 (n − 2)!+… + (−1)r Cnr (n − r)!+…
+(−1)n Cnn 0! = n!(1−1+ | 1 | +… + (−1)r | 1 |
| +… + (−1)n | 1 | ) = | ||
| r! |
| |||||||
| 2! |
| n! | ||||||
n | 1 |
|
|
|
|
|
|
|
|
= n!∑(−1)r |
|
|
|
|
|
|
|
| |
r! |
|
|
|
|
| ||||
r =2 |
|
|
|
|
| ||||
Лемма 4. |
|
|
|
|
| ||||
n |
|
|
|
|
|
|
|
|
|
∑(−1)k −r CnkCkr = 0, n, r N, n ≥ r |
|
|
| (4.2) | |||||
k =r |
|
|
|
|
|
|
|
|
|
Доказательство. Рассмотрим тождество |
|
| |||||||
n |
|
|
|
|
|
|
|
|
|
(1 + x)n = ∑Cnk xk |
|
|
| (4. | |||||
2 (вспомогательная)
3)k =0
15
Дифференцируя (4.3) r раз по x, получим
|
|
|
|
| n |
| |
n(n −1)…(n − r +1)(1 + x)n−r = ∑Cnk k(k −1)…(k − r +1)xk −r . | |||||||
|
|
|
|
| k =r |
| |
Последнее равенство преобразуется к виду | |||||||
| n! |
| n |
| k! |
|
|
| (1+ x)n−r = ∑Cnk |
| xk −r . | ||||
| (n −r)! |
| (k −r)! | ||||
| k =r |
|
| ||||
Разделив обе части на r! приходим к соотношению | |||||||
|
|
| n |
|
|
|
|
Cnr (1 + x)n−r = ∑Cnk Ckr xk | −r , |
| |||||
|
|
| k =r |
|
|
|
|
которое при x = −1 дает |
| ||||||
| n |
|
|
|
|
| |
∑(−1)k −r Cnk Ckr = 0 . |
|
|
|
| |||
| k =r |
|
|
|
|
| |
Лемма 4.3. Пусть дано N элементов и n свойств s1,…,sn. Пусть Ni1…ir — число элементов, обладающих по крайней мере свойствами
i1,…,ir, r =1, n . Тогда число элементов N(r), обладающих ровно r свойствами определяются формулой
N (r) = ∑ Ni1 …ir + | + (−1)s−r Csr | ∑ | Ni1 …is + |
1≤i1 <…<is ≤n | 1≤i1 | <…<is ≤n | (4.4) |
| n |
| |
+ (−1)n−r Cnr N12…n = ∑(−1)n−s Csr | ∑ | Ni1 …is . | |
| s=r | 1≤i1 <. | |
..<is ≤nДоказательство. В левой части (4.4) элемент с ровно r свойствами учитываются один раз. В правой части (4.4) элемент с ровно r свойствами учитываются один раз в первом слагаемом и не учитываются далее. Элемент с ровно t свойствами, t>r, учитывается
(−1)s−r CsrCts раз в слагаемом (−1)s−r Csr ∑ Ni1 …is .
1≤i1 <…<is ≤n
Поэтому вклад от элементов с ровно t свойствами, t>r, состав-
t
ляет∑(−1)s−r Csr Cts . В силу леммы 4.2 эта сумма равна нулю.
s=r
Пример 4.3 (задача о встречах). Определить количество перестановок a1,…,an чисел 1,…,n , для которых ai=i ровно в r местах.
16
Числа Белла
|
|
|
|||||||||||||||||||||||||||
Первые полторы тысяч разложений.
Угол между ними.
Матрица смежности онлайнВосьмое Нечётное Число, Восьмое Составное Число, Четвёртое Число Белла, Число Мерсенна
Решение этого кроссворда состоит из 10 букв длиной и начинается с буквы П
Ниже вы найдете правильный ответ на Восьмое нечётное число, восьмое составное число, четвёртое число Белла, число Мерсенна, если вам нужна дополнительная помощь в завершении кроссворда, продолжайте навигацию и воспользуйтесь нашей функцией поиска.
ответ на кроссворд и сканворд
Воскресенье, 15 Марта 2020 Г.
ПЯТНАДЦАТЬ
предыдущий следующий
ты знаешь ответ ?
ответ:
связанные кроссворды
- Пятнадцать
- Числа, натуральное число, расположенное между числами 14 и 16
похожие кроссворды
- Нечетное число
- Восьмое света буквы
- Восьмое воплощение бога вишну в индуизме
- Чётное или нечётное 5 букв
- Нечётное 5 букв
- Чётное, нечётное 5 букв
- Нечётное 5 букв
- Число, делящееся на данное целое число без остатка
- Число, от прибавления которого никакое число не меняется 4 буквы
Номер звонка — frwiki.
wikiДля одноименных статей см. Bell .
В математике , то п — й Колокол номер (названный в честь Эрик Темпл Белл ) является количество разделов набора с п различных элементов , или, что то же самое, число отношений эквивалентности на таком множестве.
Резюме
- 1 Первые объекты
- 2 Генератор серии
- 3 Другая недвижимость
- 4 См. Также
- 5 Примечания и ссылки
- 6 Библиография
Первые свойства
- Эти числа образуют последовательность целых чисел A000110 из OEIS , первые члены которой можно вычислить вручную:
B0знак равно1,B1знак равно1,B2знак равно2,B3знак равно5,B4знак равно15,B5знак равно52,B6знак равно203,B7знак равно877,…{\ Displaystyle B_ {0} = 1, \ quad B_ {1} = 1, \ quad B_ {2} = 2, \ quad B_ {3} = 5, \ quad B_ {4} = 15, \ quad B_ { 5} = 52, \ quad B_ {6} = 203, \ quad B_ {7} = 877, \ quad \ ldots} Первый имеет значение 1, потому что в пустом наборе есть ровно один раздел : пустой раздел, не состоящий из частей.
{n} {n \ select k} B_ {k},}что можно продемонстрировать следующим образом:
зафиксировав элемент x в наборе с n + 1 элементами, мы сортируем разделы по количеству k элементов вне части, содержащей x .
Поэтому для каждого значения k от 0 до n мы должны выбрать k элементов среди n элементов, отличных от x , а затем дать им разбиение. - Семь меньшие цифры Bell первым являются B 2 = 2, B 3 = 5, B 7 = 877, B 13 = 27644437, B 42 = 35 742 549 198 872 617 291 353 508 656 626 642 567, В 55 = 359 334 085 968 622 831 041 960 188 598 043 661 065 388 726 959 079 837 и B 2841 (см. Комплекты A051131 и A051130 OEIS). Неизвестно, есть ли другие.
{n} {n \ select k} B_ {k},}что можно продемонстрировать следующим образом: Генератор серии
Чтобы обработать все числа Белла, мы можем взглянуть на связанный генератор и ряды экспоненциального генератора , которые соответственно:
{{\ frac {n} {W (n)}} — n-1},}где W — W-функция Ламберта ; получается менее точное приближение, но более удобное в использовании с помощью обрамления ; можно также заметить сходство предыдущего приближения с формулой Стирлинга . перИкс-перперИкс<W(Икс)<перИкс{\ Displaystyle \ пер Икс- \ пер \ пер Икс <W (х) <\ пер х}
Смотрите также
- Эти номера Bell упорядоченные , которые идентифицируют заказанные разделы.
- Белл треугольник , который позволяет просто получить номера Bell
Примечания и ссылки
- ↑ Элементы множества всегда различны в обычной теории множеств , но это не так в теории мультимножеств . И количество разделов набора с n неотличимыми элементами — это количество разделов целого числа .
- ↑ (in) А.К. Эйткен , « Проблема комбинаций » , Математические заметки , Vol. 28,, xviii — xxiii ( ISSN 1757-7489 и 2051-204X , DOI 10.1017 / S1757748900002334 , читать онлайн , по состоянию на 29 мая 2021 г. )
- ↑ Дональд Кнут , Искусство программирования : история комбинаторного поколения , т. 4, фас. 4, Эддисон Уэсли,
- ↑ Даниэль Барски и Бенали Бензаго , « Белловые числа и сумма факториалов », Journal de Théorie des Nombres de Bordeaux , vol. 16,, стр. 1-17 ( читать онлайн [PDF] )
- ↑ Мы найдем другие приближения B n на (в) Эрике В. Вайсштейне , » Bell Number » на MathWorld .
28,, xviii — xxiii ( ISSN 1757-7489 и 2051-204X , DOI 10.1017 / S1757748900002334 , читать онлайн , по состоянию на 29 мая 2021 г. )
Вайсштейне , » Bell Number » на MathWorld .Библиография
- Дональд Кнут , Искусство программирования : история комбинаторного поколения , т. 4, фас. 3, Эддисон Уэсли,
<img src=»https://fr.wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»» title=»»>
ДНК-диагностика синдрома Мартина-Белла (ломкой Х-хромосомы)
ЦЕНЫ*Цены для иностранных граждан уточнять по телефону либо по e-mail
Уважаемые пациенты, Цены на услуги могут изменяться и отличаться от цены на сайте, действительную стоимость услуг уточняйте у администратора.
Дородовая диагностика
Пренатальная ДНК-диагностика нейросенсорной несиндромальной тугоухости (по ворсинам хориона или амниоцитам)
5 410,00
Пренатальная ДНК-диагностика муковисцидоза (по ворсинам хориона или амниоцитам)
5 820,00
Пренатальная ДНК-диагностика синдрома Мартина-Белл (ломкой Х-хромосомы) (по ворсинам хориона или амниоцитам)
9 560,00
Пренатальная ДНК-диагностика спинальной мышечной атрофии (по ворсинам хориона или амниоцитам)
4 940,00
Пренатальная ДНК-диагностика принадлежности резуса эмбриону (по ворсинам хориона или амниоцитам)
4 990,00
Пренатальная ДНК-диагностика фенилкетонурии (по ворсинам хориона или амниоцитам)
5 260,00
Пренатальное определение пола плода при Х-сцепленных заболеваниях (по ворсинам хориона или амниоцитам)
1 610,00
ДНК-тест на материнскую контаминацию
4 740,00
Определение кариотипа амниоцитов беременности, которая развивается
3 690,00
Определение кариотипа развивающейся беременности, FISH-метод
4 500,00
Определение кариотипа ворсин хориона в абортивном материале
3 600,00
Определение кариотипа ворсин хориона беременности, которая развивается
3 420,00
Определение кариотипа ворсин хориона беременности, которая развивается, FISH-метод
3 890,00
Определение кариотипа плода из пуповинной крови
3 040,00
Молекулярно-диагностические исследования
Выделение и хранение ДНК из лейкоцитов периферийной крови
540,00
Определение зиготности гена RHD
2 720,00
Определение мутаций генов BRCA1 и BRCA2
3 500,00
ДНК-диагностика неустановленной мутации (І ст.
сложности)
14 000,00
ДНК-диагностика неустановленной мутации (ІІ ст. сложности)
28 000,00
ДНК-диагностика неустановленной мутации (ІІІ ст. сложности)
42 000,00
ДНК-диагностика микроделеций Y-хромосомы
1 940,00
ДНК-диагностика микроструктурных хромосомных аномалий методом сравнительной геномной гибридизации
48 800,00
Предимплантационная генетическая диагностика, сравнительная геномная гибридизация, 24 хромосомы, количество эмбрионов не больше 8-ми
66 980,00
Предимплантационная генетическая диагностика, сравнительная геномная гибридизация, 24 хромосомы, количество эмбрионов не больше 8-ми, без биопсии бластоцисты/бластомера
64 080,00
Предимплантационная генетическая диагностика: сравнительная геномная гибридизация, 24 хромосомы, за каждый дополнительный эмбрион свыше 8-ми.
8 900,00
Предимплантационная генетическая диагностика методом ПЦР (I ст. сложности)
14 000,00
Предимплантационная генетическая диагностика методом ПЦР (ІI ст.
сложности)
28 000,00
Предимплантационная генетическая диагностика методом ПЦР (ІII ст. сложности)
42 000,00
ДНК-диагностика муковисцидоза
2 170,00
ДНК-диагностика нейросенсорной несиндромальной тугоухости (ген GJB2)
1 220,00
ДНК-диагностика синдрома Мартина-Белл (ломкой X -хромосомы)
6 520,00
ДНК-диагностика спинальной мышечной атрофии
1 260,00
ДНК-диагностика фенилкетонурии
1 720,00
Неинвазивная пренатальная ДНК-диагностика резус-фактора плода (по крови беременной)
8 040,00
Пренатальная ДНК-диагностика нейросенсорной несиндромальной тугоухости (по ворсинам хориона или амниоцитам)
5 410,00
Пренатальная ДНК-диагностика муковисцидоза (по ворсинам хориона или амниоцитам)
5 820,00
Пренатальная ДНК-диагностика синдрома Мартина-Белл или ломкой Х-хромосомы (по ворсинам хориона или амниоцитам)
9 560,00
Пренатальная ДНК-диагностика спинальной мышечной атрофии (по ворсинам хориона или амниоцитам)
4 940,00
Пренатальная ДНК-диагностика принадлежности резуса эмбриона (по ворсинам хориона или амниоцитам)
4 990,00
Пренатальная ДНК-диагностика фенилкетонурии (по ворсинам хориона или амниоцитам)
5 260,00
Пренатальное определение пола плода при Х-сцепленных заболеваниях (по ворсинам хориона или амниоцитам)
1 610,00
ДНК-тест на материнскую контаминацию
4 740,00
Программа для будущих родителей «Ответственное родительство» (ДНК-диагностика муковисцидоза, ДНК-диагностика спинальной мышечной атрофии)
7 440,00
Программа для будущих родителей «Ответственное родительство» РАСШИРЕННАЯ (ДНК-диагностика 289 генов)
15 750,00
Программа для будущих родителей «Ответственное родительство» РАСШИРЕННАЯ для второго партнера (ДНК-диагностика 289 генов)
15 750,00
HLA-типирование (2 лица)
16 640,00
HLA-типирование (1 лицо)
8 425,00
НИПТ SAGE NADIYA — неинвазивная диагностика хромосомных аномалий плода (по крови беременной женщины)
16 000,00
ПОСМОТРЕТЬ ВСЕ ЦЕНЫ Партнер клиники — родильный дом «Лелека»ЗАПИСАТЬСЯ
k A_i=S$ и для каждого $i\not=j$, $A_i\cap A_j=\emptyset$.
$\квадрат$Пример 1.4.2. Разбиения множества $\{a,b,c\}$ равны $\{\{a\},\{b\},\{c\}\}$, $\{\{a,b\},\{c\}\}$, $\{\{a ,с\},\{б\}\}$, $\{\{b,c\},\{a\}\}$ и $\{\{a,b,c\}\}$. $\квадрат$
Разделы возникают в ряде областей математики. Например, если $\equiv$ — отношение эквивалентности на множестве $S$, эквивалентность классы $\equiv$ образуют раздел $S$. Здесь мы считаем число разбиений конечного множества $S$, которые мы могли бы также считать $[n]=\{1,2,3,\ldots,n\}$, если не представляет интерес какой-либо другой набор. Обозначим количество разделов $n$-элемента множества $B_n$; эти 9n {n\выберите k} B_k. $$
Доказательство. Рассмотрим разбиение $S=\{1,2,\ldots,n+1\}$, $A_1$,…,$A_m$. Мы
можно предположить, что $n+1$ находится в $A_1$ и что $|A_1|=k+1$ для некоторого
$k$, $0\le k\le n$. Тогда $A_2$,…,$A_{m}$ образуют раздел
остальные $n-k$ элементов $S$, то есть $S\backslash A_1$. Есть
$B_{n-k}$ разделов этого множества, значит, существует $B_{n-k}$ разделов
$S$, в котором одной частью является множество $A_1$.
n {n\выберите k} B_k,
$$
написано наоборот.
$\qed$
93 {3\выберите k}B_k = 1\cdot 1 + 3\cdot 1 + 3\cdot 2 +
1\cточка 5 = 15\кр
}
$$
$\квадрат$
Числа Белла растут экспоненциально быстро; первые несколько 1, 1, 2, 5, 15, 52, 203, 877, 4140, 21147, 115975, 678570, 4213597, 27644437.
Числа Белла появляются во многих других задачах; вот
интересный пример. Обычная потребность в некоторых компьютерных программах состоит в том, чтобы
генерировать случайную перестановку $1,2,3,\ldots,n$, которую мы можем подумать
как перетасовка чисел, визуализированная как пронумерованные карты в
палуба. Вот привлекательный метод, который легко запрограммировать: Начните с
числа по порядку, затем на каждом шаге убирайте одно число случайным образом
(это легко сделать в большинстве языков программирования) и поместите его на передний план
из списка номеров. (Рассматриваемый как перетасовка колоды карт, это
соответствует удалению карты и помещению ее на верх колоды.)
Сколько раз мы должны это сделать? Волшебного числа нет, но оно
конечно, не должен быть маленьким по сравнению с размером $n$.
m$.) Так как существует
всего $n!$ различных перестановок $1,2,\ldots,n$, это означает
что многие перетасовки дают один и тот же окончательный порядок.
Вот наш вопрос: сколько перетасовок приводит к исходному порядку?
Пример 1.4.6. Эти перетасовки возвращаются к исходному порядку: $(1,1,1,1,1)$, $(5,4,3,2,1)$, $(4,1,3,2,1)$. $\квадрат$
Теорема 1.4.7 Количество перетасовок $[n]$, в результате которых исходный порядок сортировки $B_n$.
Доказательство. Поскольку мы знаем, что $B_n$ подсчитывает количество разделов
$\{1,2,3,\ldots,n\}$, мы можем доказать теорему, установив 1–1
соответствие между тасовками, которые оставляют колоду отсортированной, и
перегородки. Учитывая перетасовку $(m_1,m_2,\ldots,m_n)$, мы помещаем в
single устанавливает все $i$ так, что $m_i$ имеет единственное значение. Например,
используя перетасовку $(4,1,3,2,1)$, так как $m_2=m_5$, один набор
$\{2,5\}$. Все остальные значения различны, поэтому другие наборы в
раздела: $\{1\}$, $\{3\}$ и $\{4\}$.
Обратите внимание, что каждое перемешивание, независимо от окончательного порядка, производит разделить этим методом. Нас интересуют только те перетасовки, которые оставьте колоду в порядке. Теперь нам нужно показать, что каждый раздел результат ровно одной такой перетасовки.
Предположим, у нас есть раздел с $k$ частями. Если при тасовке колода остается отсортированной, последняя запись, $m_n$, должна быть 1. Если часть, содержащая $n$, равна $A_1$, то она должна быть такой $m_i=1$ тогда и только тогда, когда $i\in A_1$. Если $k=1$, то единственная часть содержит все $\{1,2,\ldots,n\}$, и перетасовка должна быть $(1,1,1,\ldots,1)$.
Если $k>1$, последний ход, отличный от 1, должен быть 2, так как 2 должно закончиться
сразу после 1. Таким образом, если $j_2$ — наибольший индекс такой, что
$j_2\notin A_1$, пусть $A_2$ — часть, содержащая $j_2$, и она должна быть
что $m_i=2$ тогда и только тогда, когда $i\in A_2$. Продолжаем так: Один раз
мы выяснили, какие из $m_i$ должны иметь значения $1,2,\ldots,p$,
пусть $j_{p+1}$ будет наибольшим индексом таким, что
$j_{p+1}\notin A_1\cup\cdots\cup A_p$, пусть $A_{p+1}$ — часть
содержащий $j_{p+1}$, а затем $m_i=p+1$ тогда и только тогда, когда $i\in
А_{р+1}$.
n$, и это оказывается немного больше, чем
$1/n!$. Таким образом, это не подходящий метод для генерации случайных
перестановки.
Приведенное выше рекуррентное соотношение представляет собой несколько громоздкий способ вычисления Звонковые числа. Другой способ их вычисления — с другим рецидив, выраженный в Треугольник колокола, конструкция которого аналогична треугольник Паскаля: $$\матрица{ А_{1,1}\кр А_{2,1}&А_{2,2}\кр А_{3,1}&А_{3,2}&А_{3,3}\кр A_{4,1}&A_{4,2}&A_{4,3}&A_{4,4}\cr} \qquad\matrix{ 1\кр 1&2\кр 2&3&5\кр 5&7&10&15\кр} $$ Правило построения этого треугольника: $A_{1,1}=1$; первый запись в каждой строке является последней записью в предыдущей строке; другие записи $A_{n,k}=A_{n,k-1}+A_{n-1,k-1}$; строка $n$ содержит $n$ записей. Оба первый столбец и диагональ состоят из чисел Белла, с $A_{n,1}=B_{n-1}$ и $A_{n,n}=B_n$.
$A_{n,k}$ можно интерпретировать как количество разделов
$\{1,2,\ldots,n+1\}$ в
который $\{k+1\}$ является набором синглетонов с самой большой записью в разделе.
Например, $A_{3,2}=3$; разбиения $3+1=4$, в которых $2+1=3$
это наибольшее число, появляющееся в одноэлементном наборе,
$\{\{1\},\{2,4\},\{3\}\}$, $\{\{2\},\{1,4\},\{3\}\} $ и $\{\{1,2,4\},\{3\}\}$.
Чтобы увидеть, что это действительно работает так, как рекламируется, нам нужно подтвердить несколько вещи. Во-первых, рассмотрим $A_{n,n}$, число разделов $\{1,2,\ldots,n+1\}$, в котором $\{n+1\}$ — одноэлементное множество с самая большая запись в разделе. Так как $n+1$ — наибольший элемент множества, все разбиения, содержащие один элемент $\{n+1\}$, удовлетворяют требование, и поэтому $B_n$ разделов $\{1,2,\ldots,n\}$ вместе с $\{n+1\}$ представляют собой в точности интересующие нас разбиения, которые есть, $A_{n,n}=B_n$.
Далее проверяем, что при желаемой интерпретации действительно
верно, что $A_{n,k}=A_{n,k-1}+A_{n-1,k-1}$ для $k>1$. Рассмотрим
раздел считается $A_{n,k-1}$. Это содержит синглтон $\{k\}$,
и элемент $k+1$ не является одноэлементным. Если мы поменяем местами $k$ и
$k+1$, мы получаем одноэлементный $\{k+1\}$, и ни один больший элемент не находится в
синглтон.
2$ делит $n$; Другими словами, числа без квадратов являются произведениями
различных простых множителей, то есть $n=p_1p_2\cdots p_k$, где каждый
$p_i$ — простое число, и никакие два простых множителя не равны.
Найдите количество факторизаций $n$. Например, $30=2\cdot
3\cdot 5$, а факторизация 30 равна 30, $6\cdot 5$, $10\cdot
3$, $2\cdot 15$ и $2\cdot 3\cdot 5$. Обратите внимание, что мы считаем только 30 как
факторизация, хотя в некотором смысле и тривиальная факторизация.
Пример 1.4.3 Схема рифмовки строфы стихотворения указывает, какие строки
рифма. Обычно это выражается в форме ABAB, что означает первый
и третьи строки четырехстрочной строфы рифмуются, как и вторая и
четвертая, или ABCB, означающая, что рифмуются только вторая и четвертая строки, и так далее. А
лимерик — пятистрочное стихотворение со схемой рифмовки AABBA. Как много
возможны разные схемы рифмовки для строфы из $n$ строк? Избегать
повторяющиеся шаблоны, мы допускаем новую букву в шаблон только тогда, когда
все предыдущие буквы использовались слева от новой.
За
Например, ACBA не допускается, так как когда C помещается в позицию 2, B
слева не использовался. Это та же схема рифмовки, что и ABCA,
что разрешено.
9nS(n,k),
$$
где $S(n,k)$ — количество разбиений $\{1,2,\ldots,n\}$ на
ровно $k$ частей, $1\le k\le n$. $S(n,k)$ — это Числа Стирлинга второго рода .
Найдите рекуррентное соотношение для
$S(n,k)$. Ваше повторение должно позволять довольно простой треугольник
построение, содержащее значения $S(n,k)$, а затем числа Белла
можно вычислить, суммируя строки этого треугольника. Показать первый
пять рядов треугольника, $n\in\{1,2,\ldots,5\}$.
Пример 1.4.5 Пусть $A_n$ — количество разделов
$\{1,2,\ldots,n+1\}$, в котором ни одно последовательное целое не находится в одном и том же
часть перегородки. Например, при $n=3$ эти разделы
$\{\{1\},\{2\},\{3\},\{4\}\}$, $\{\{1\},\{2,4\},\{3 \}\}$,
$\{\{1,3\},\{2\},\{4\}\}$, $\{\{1,3\},\{2,4\}\}$,
$\{\{1,4\},\{2\},\{3\}\}$, поэтому $A_3=5$.
Пусть $A(n,k)$ — количество разделов
$\{1,2,\ldots,n+1\}$ ровно на $k$ частей, в которых нет последовательных
целые числа находятся в одной части раздела.
{n+1} A(n,k).
$$
Найдите повторение для $A(n,k)$ и покажите, что $A_n=B_n$.
Больше дискретной математики через теорию графов
\( \def\negchoose#1#2{\genfrac{[}{]}{0pt}{}{#1}{#2}_{-1}}
\newcommand{\mchoose}[2]{\left(\!\binom{#1}{#2}\!\right)}
\newcommand{\cycle}[1]{\arraycolsep 5 pt
\left(\begin{массив}#1\конец{массив}\right)}
\newcommand{\importantarrow}{\Rightarrow}
\newcommand{\qchoose}[2]{\left[{#1\top#2}\right]_q}
\ новая команда {\ bp} {
\begin{enumerate}{\setcounter{enumi}{\value{номер_проблемы}}}}
\newcommand{\ep}{\setcounter{номер_проблемы}{\значение{enumi}}
\конец{перечислить}}
\ новая команда {\ игнорировать} [1] {}
\renewcommand{\bottomfraction}{.8}
\renewcommand{\topfraction}{.8}
\newcommand{\apple}{\text{🍎}}
\newcommand{\ap}{\яблоко}
\newcommand{\банан}{\текст{🍌}}
\ новая команда {\ ba} {\ банан}
\newcommand{\груша}{\текст{🍐}}
\newcommand{\pe}{\груша}
\DeclareMathOperator{\Fix}{Fix}
\DeclareMathOperator{\Orb}{Orb}
\newcommand{\F}{\mathcal{F}}
\новая команда{\предупреждение}{\fbox}
\def\d{\displaystyle}
\def\курс{Математика 228}
\ новая команда {\ f} [1] {\ mathfrak # 1}
\ новая команда {\ s} [1] {\ mathscr # 1}
\def\N{\mathbb N}
\def\B{\mathbf{B}}
\def\circleA{(-.
{-1}}
\def\nrml{\triangleleft}
\ деф \ ст {:}
\ деф \ ~ {\ широкая тильда}
\def\rem{\mathcal R}
\def\sigalg{$\sigma$-алгебра }
\def\Гал{\mbox{Гал}}
\def\iff{\leftrightarrow}
\def\If{\Leftrightarrow}
\ деф \ земля {\ клин}
\def\И{\bigwedge}
\защита\вход{\вход}
\def\AAnd{\d\bigwedge\mkern-18mu\bigwedge}
\def\Ви{\bigvee}
\def\VVee{\d\Vee\mkern-18mu\Vee}
\ деф \ имп {\ стрелка вправо}
\def\Imp{\Rightarrow}
\def\Fi{\Leftarrow}
\def\var{\mbox{var}}
\def\Th{\mbox{Th}}
\защита\вход{\вход}
\def\sat{\mbox{Sat}}
\def\con{\mbox{Con}}
\def\iffmodels{\bmodels\models}
\def\dbland{\bigwedge \!\!\bigwedge}
\def\дом{\mbox{дом}}
\def\rng{\mbox{диапазон}}
\def\isom{\cong}
\DeclareMathOperator{\wgt}{wgt}
\newcommand{\vtx}[2]{узел[заливка,круг,внутренний интервал=0pt, минимальный размер=4pt,метка=#1:#2]{}}
\ новая команда {\ va} [1] {\ vtx {выше} {# 1}}
\ новая команда {\ vb} [1] {\ vtx {ниже} {# 1}}
\ новая команда {\ vr} [1] {\ vtx {право} {# 1}}
\ новая команда {\ vl} [1] {\ vtx {слева} {# 1}}
\renewcommand{\v}{\vtx{выше}{}}
\def\circleA{(-.
5,0) круг (1)}
\def\circleAlabel{(-1.5,.6) узел[выше]{$A$}}
\def\circleB{(.5,0) круг (1)}
\def\circleBlabel{(1.5,.6) узел[выше]{$B$}}
\def\circleC{(0,-1) круг (1)}
\def\circleClabel{(.5,-2) узел[справа]{$C$}}
\def\twosetbox{(-2,-1.4) прямоугольник (2,1.4)}
\def\threesetbox{(-2.5,-2.4) прямоугольник (2.5,1.4)}
\def\ansfilename{практика-ответы}
\def\shadowprops{{fill=black!50,shadow xshift=0.5ex,shadow yshift=0.5ex,path fading={круг с размытым краем 10 процентов}}}
\ новая команда {\ hexbox} [3] {
\def\x{-cos{30}*\r*#1+cos{30}*#2*\r*2}
\def\y{-\r*#1-sin{30}*\r*#1}
\рисовать (\х,\у) +(90:\r) — +(30:\r) — +(-30:\r) — +(-90:\r) — +(-150:\r) — +(150: \r) — цикл;
\draw (\x,\y) узел{#3};
}
\newcommand{\card}[1]{\left| #1 \справа|}
\newcommand{\twoline}[2]{\begin{pmatrix}#1 \\ #2 \end{pmatrix}}
\новая команда{\lt}{<}
\новая команда{\gt}{>}
\newcommand{\amp}{&}
\)
Число Белла, \(B_{k}\text{,}\), обозначает количество способов, которыми множество \(k\) объектов может быть разделено на непустые подмножества.
kS(k,n)\text{.}\)
Последовательность номеров Белла начинается с
\begin{уравнение*} 1, 1, 2, 5, 15, 52, 203, 877, 4040, 21147, 115975, \ldots \end{уравнение*}
Обратите внимание, что первые четыре цифры выглядят как каталонские. Фактически, одна из многих вещей, которые подсчитывают каталонские числа, — это непересекающихся наборов разделов. Как только вы поверите в это, вы увидите, что \(C_n \le B_n\) для всех \(n\text{.}\)
Числа Белла могут быть получены путем построения так называемого треугольника Белла. Чтобы построить этот треугольник, начните с 1 вверху и 1 под ним. Сложите эти два числа вместе и поставьте сумму 2 справа от 1 во втором столбце. Эта цифра 2 также является первой записью третьей строки. Вторая запись в третьей строке находится путем прибавления 2 к числу 1 над ней. Эта сумма равна 3 и идет справа от 2. 3 теперь ниже 2. Сложение этих двух чисел дает последнее число 5 в третьей строке. Поскольку над цифрой 5 нет числа, третья строка завершена.
5 теперь становится первым числом в четвертой строке, и процесс продолжается.
| 1 | ||||||
| 1 | 2 | |||||
| 2 | 3 | 5 | ||||
| 5 | 7 | 10 | 15 | |||
| 15 | 20 | 27 | 37 | 52 | ||
| 52 | 67 | 87 | 114 | 151 | 203 | |
| 203 | 255 | 322 | 409 | 523 | 674 | 877 |
Подводя итог, можно сказать, что построение треугольника следует двум основным правилам:
Последнее число каждой строки является первым числом следующей строки.
Все остальные числа находятся путем прибавления числа слева от пропущенного числа к числу непосредственно над этим же числом.
Когда треугольник расширяется, как указано выше, номера колоколов находятся как в первом столбце, так и по внешней диагонали.
Активность297
Почему эта конструкция треугольника дает вам числа Белла? Объясните с точки зрения набора разделов.
Как и треугольник Паскаля, треугольник Белла обладает несколькими интересными свойствами.
Активность298
Если сумма ряда прибавляется к номеру Белла в конце этой строки, получается следующий номер Белла. Например, сумма четвертой строки плюс число Белла в конце строки: \(15 + 20 + 27 + 37 + 52 + 52\) равно 203, следующему числу Белла. Почему это происходит?
Активность299
Еще одна закономерность, которую вы можете заметить: числа второй диагонали \(1, 3, 10, 37, 151, 674, \ldots\) являются суммами горизонтальных рядов. Докажи это!
Слегка повернув треугольник, мы получим треугольник разности , аналогичный треугольнику Паскаля. Записи, которые формируются рекурсивно путем сложения в треугольнике Паскаля, теперь являются разностью двух чисел над ними в треугольнике Белла.
| 1 | 2 | 5 | 15 | 52 | 203 | 877 | \(\ldots\) | ||||||
| 1 | 3 | 10 | 37 | 151 | 674 | \(\ldots\) | |||||||
| 2 | 7 | 27 | 114 | 523 | \(\ldots\) | ||||||||
| 5 | 20 | 87 | 409 | \(\ldots\) | |||||||||
| 15 | 67 | 322 | \(\ldots\) | ||||||||||
| 52 | 255 | \(\ldots\) | |||||||||||
| 203 | \(\ldots\) |
Активность300
Объясните, почему различия работают именно так, как в повернутом треугольнике.
{\text{th}}\) может быть рекурсивно представлено как \(B_{n + 1} = \binom{n}{0} B_{ 0} + \binom{n}{1} B_{1} + \binom{n}{2}B_{2} + \ldots + \binom{n}{n} B_{n}\text{.}\ ) Коэффициенты этого уравнения являются элементами \(n\)-й строки треугольника Паскаля.
Активность301
Доказать повторяемость
\begin{уравнение*} B_{k + 1} = \binom{k}{0} B_{0} + \binom{k}{1} B_{1} + \binom{k}{2}B_{2} + \ldots + \ бином {к} {к} В_ {к} \end{equation*}
Числа Белла связаны с числами Стирлинга и могут быть определены как сумма чисел Стирлинга второго рода. То есть \(B_{k} = S(k,1) + S(k,2) + \cdots + S(k,k)\text{,}\), где \(S(k,n)\ ) представляет количество способов группировки \(k\) элементов в \(n\) подмножеств. Итак, \(B_{3} = S(3,1) + S(3,2) + S(3,3) = 1 + 3 + 1 = 5\text{.}\) Поскольку числа Белла учитывают разбиения набора элементов, они используются в теории простых чисел для перечисления количества способов разложения числа на множители с различными простыми множителями.
Например, число 42 имеет три различных простых делителя: 2, 3 и 7. Поскольку \(B_{3} = 5\) , мы знаем, что существует пять способов разложения 42 на множители. Это \(2 \times 3 \times 7 \text{,}\) \(2 \times 21\text{,}\) \(3 \times 14\text{,}\) \(6 \times 7\text{,}\) и \(42 \text{.}\) Таким образом, число \(210\text{,}\), имеющее 4 различных делителя, 2, 3, 5 и 7, можно разложить на множители \(B_{4} = 15\) способов .
Числа Белла можно использовать для моделирования многих реальных ситуаций. Например, количество различных способов, которыми два человека могут спать на немаркированных односпальных кроватях, равно \(B_{2} = 2\) способов: они могут спать в одной кровати или в разных кроватях. Количество способов сервировки обеда, состоящего из трех блюд, таких как салат, хлеб и рыба, равно \(B_{3} = 5\) способов: каждое можно подать на отдельной тарелке, салат и хлеб — на одна тарелка и рыба на другой, салат и рыба на одной тарелке и хлеб на другой, или все три блюда могут быть на одной тарелке.
Этот пример служит моделью для пяти способов, которыми три человека могут занимать три немаркированные кровати, пяти способов, которыми трое заключенных могут быть скованы вместе наручниками, пяти способов, которыми три нации могут образовывать союзы, или любой ситуации разделения трех отдельных элементов на непустые. подмножества.
Одним из интересных применений чисел Белла является подсчет количества схем рифмовки, возможных для строфы в стихах. Есть \(B_{2} = 2\) возможностей для двухстрочной строфы: строки могут либо рифмоваться, либо не рифмоваться. Возможные схемы рифмовки трехстрочной строфы можно описать как ааа, ааб, аба, абб и абв: таким образом, существует 5 или \(B_{3}\) возможных схем рифмовки. Японцы использовали диаграммы, изображающие возможные схемы рифмовки пятистрочной строфы \(B_{5} = 52\), еще в 1000 г. н.э. в 9 в.0099 Сказка о Гэндзи Леди Шикибу Мурасаки.
Завершаем интересным занятием.
Активность302
Набор \(\{u_{0}, u_{1}, u_{2}, \ldots \}\), где \(u_{0} = 1\text{,}\) \(u_{1} = x\text{,}\) \(u_{2} = x(x — 1)\text{,}\) \(u_{3} = x(x — 1)(x — 2)\text{ ,}\) и т.
д., является базисом векторного пространства \(V\) всех многочленов с действительными коэффициентами. Пусть \(P(x) = c_{0}u_{0} + c_{1}u_{1} + c_{2}u_{2} + \cdots\) будет любым элементом \(V\text{, }\) и определим функционал \(L\) следующим образом: \(L\lbrack P(x)\rbrack = c_{0} + c_{1} + \cdots\text{.}\) 9{n}\rbrack\) .
Получите рекурсию в действии 301, используя предыдущую часть.
Вычисление чисел Белла
fredrikj.net / blog /
6 августа 2015 г.
Числа Белла $B_n$ подсчитывают количество способов множество из $n$ элементов можно разбить на непересекающиеся подмножества. целочисленная последовательность $B_0, B_1, \ldots$ (OEIS A000110) начинается с $$1, 1, 2, 5, 15, 52, 203, 877, 4140, 21147, \ldots$$
Легко видеть, что $B_n \le n!$ по индукции. Разбиение множества $A = \{a_1, \ldots, a_{n-1}\}$ можно продолжить до разбиения множества $A \cup \{a_n\}$ не более чем на $n$ различных способами: мы можем либо добавить $a_n$ к одному из существующих подмножеств (которых не более $n-1$), либо создать новое подмножество, содержащее только $a_n$.
{W(x)} = x$.
9{2+o(1)}$, т.е.
квазиквадратичны по размеру результата.
Точное вычисление чисел Белла
Самый простой способ вычислить числа Белла — это использовать числовой треугольник напоминающий треугольник Паскаля для биномиальных коэффициентов. Числа Белла появляются на краях треугольника. Начиная с 1, каждая новая строка в треугольнике строится путем взятия последней записи в предыдущей строке как первая запись, а затем установка каждого новая запись для своего левого соседа плюс его верхний левый сосед: 9{1+o(1)}$ раз. Сочетание EGF с многомодульной оценкой для вычисления целые числа $B_0, \ldots, B_n$ одновременно весьма привлекательны поскольку он избегает знаменателей факторного размера, которые мы получаем, когда выполнение арифметических действий в $Q[[x]]$.
Я реализовал большинство описанных алгоритмов выше во FLINT еще в 2011 году.
- bell_number_bsplit.c вычисляет изолированное число Белла, используя формулу Добински и двоичное разбиение
- bell_number_multi_mod. c
вычисляет изолированное число Белла, используя конечную формулу Добински и многомодульное вычисление
- bell_number_vec_recursive.c вычисляет вектор чисел Белла, используя алгоритм рекурсивного числового треугольника
- bell_number_vec_multi_mod.c вычисляет вектор чисел Белла, используя многомодульную оценку (на основе EGF по модулю малых простых чисел) 90 205
- bell_number_nmod.c вычисляет изолированное число Белла по модулю $p$, используя конечную формулу Добински
- bell_number_nmod_vec_recursive.c вычисляет вектор чисел Белла по модулю $p$, используя алгоритм рекурсивного числового треугольника
- bell_number_nmod_vec_series.c вычисляет вектор чисел Белла по модулю $p$, используя EGF
c
вычисляет изолированное число Белла, используя конечную формулу Добински и многомодульное вычислениеЕсть также по умолчанию функции FLINT, которые автоматически выбирают (примерно, в зависимости от железа) самый быстрый алгоритм.
В следующей таблице показано, сколько секунд занимает FLINT с соответствующим алгоритмом на моем ноутбуке:
| нет | vec_recursive | vec_multi_mod | бсплит | мультимод |
| 10 | 0.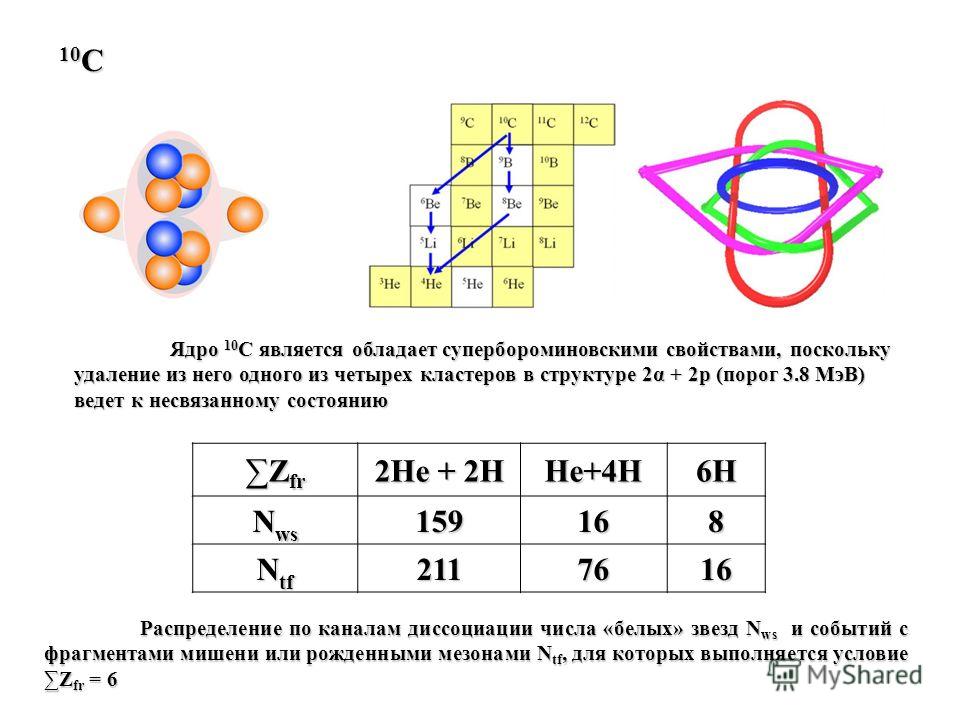 000000013* | 0.0000076 | 0.0000039 | 0.0000059 |
| 100 | 0.00011 | 0.00033 | 0.000031 | 0.000094 |
| 1000 | 0.070 | 0.30 | 0.0060 | 0,0093 |
| 10000 | 87 | 118 | 3,1 | 1,2 |
| 100000 | — | — | 858 | 164 |
Обратите внимание, что тайминги для первых двух алгоритмов предназначены для одновременного вычисления первых $n$ чисел Белла, а последние два предназначены для вычисления только $B_n$. Звездочка (*) означает, что код на самом деле обманывает здесь, используя таблицу поиска, когда $n
Мы видим, что алгоритм числового треугольника
превосходит EGF (vec_multi_mod) при разумных значениях $n$.
Алгоритм числового треугольника имеет худшую асимптотическую сложность, но намного
ниже накладные расходы.
Я не реализовал распараллеливание алгоритмов multi_mod. Это должно дать почти двукратное ускорение на моем двухъядерном процессоре.
Во FLINT нет реализации на основе OGF, но я тестировал этот алгоритм, и у него почти одинаковая скорость к EGF с многомодульной оценкой.
Приблизительный расчет числа звонков
Теперь предположим, что вместо вычисления точного значения $B_n$ мы довольны старшими цифрами $d$, где $d$ для Например, может быть 10, 100 или 1000. Ясно, что если мы рассмотрим 9{(N+1)}(m), \ldots$ и, в свою очередь, остаток ряда Тейлора.
Пусть
$$T(z) = \exp(F(z)), \quad F(z) = n \log(z) — \log \Gamma(z+1).$$
Ясно, что $|T(z)| \le \exp(|F(z)|)$.
У нас есть
$$
\sup_{|z-m|\le R} |F(z)| \le |F(m)| + R \sup_{|z-m|\le R} |F'(z)|.
$$
Однако, непосредственно ограничивая
$$
F'(z) = \frac{n}{z} — \psi(z+1)
$$
не работает, так как есть
является катастрофическим сокращением ($F'(z) \ приблизительно 0$ имеет место по построению, когда $z \ приблизительно m$).
{2+o(1)}$ точном вычислении $B_n$
(при условии, что все, что нам нужно, это числовое приближение)!
9k$, чтобы гарантировать точность результата до $d$ цифр, несмотря на ошибки округления.
Я не вижу простого способа оптимально подобрать все эти параметры априори , так как они сложным образом зависят друг от друга. Рабочая точность особенно трудно выбрать, так как это зависит от деталей, лежащих в основе алгоритмы для гамма-функции, для умножения степенных рядов, и так далее. Мое решение состояло в том, чтобы всегда выбирать отношение $r / R = 1/8$ (что дает три бита на член) и выбрав как количество подразделений и рабочая точность адаптивно: 92$$ где $p$ — точность в битах. Например:
- Чтобы вычислить 10-значное приближение $B_n$, ряд Тейлора работает быстрее, если $n$ больше 5 миллионов.
- Чтобы вычислить 100-значное приближение $B_n$, ряд Тейлора работает быстрее, если $n$ больше 500 миллионов.
- Чтобы вычислить 1000-значное приближение $B_n$, ряд Тейлора работает быстрее, если $n$ больше 50 миллиардов.
На следующем графике показано время, за которое arb_bell_fmpz для вычисления цифр от $B_n$ до $d$, где $d$ равно 10, 100, 1000 и $\infty$ (точное вычисление $B_n$). 9{100}}$, количество разделов набора с 1 элементом гугола, с точностью до 1000 цифр:
- 4784314134261851806
- Поддержка простой работы с аппроксимациями вещественных чисел с переменной точностью и автоматическое отслеживание границ их ошибок. 9k$$, который реализован в mpmath.
Задача читателю: можете ли вы придумать более быстрый способ вычисления чисел Белла (приблизительно или точно)? Насколько точно вы можете аппроксимировать $B_n$, используя асимптотические разложения, если вы использовать поправочные члены высокого порядка? Можете ли вы сделать это с помощью эффективных и строгих ограничений погрешности?
fredrikj.
net |
Индекс блога |
RSS-канал |
Подписывайтесь на меня в Твиттере |
Стать спонсоромНик Кэннон приветствует ребенка номер 10 с Бриттани Белл
У Ника Кэннона в этом году есть пара подарков на ранний день рождения, потому что он только что приветствовал своего 10-го ребенка … всего через 2 недели после рождения его 9-го ребенка.
Чрезвычайно гордый папа поделился в пятницу новостями о своем новорожденном сыне, Rise Messiah Cannon . на ИГ. Он написал: «Еще одно благословение!!! По мере того, как мое путешествие по этой планете становится все более и более замечательным и непостижимым, все, что я могу сделать, это благодарить Бога и продолжать просить Всевышнего направить мои шаги».
Райз — третий ребенок Ника от его бывшей девушки Бриттани Белл .
ТМЗ Композит
Ник Кэннон получает приветствие в честь Дня отца от трех мамочек
Затем он поблагодарил Бриттани за то, что он называет 48 часами мучительной боли и опасной для жизни опасности, сказав: «Спасибо, Бриттани, за моих маленьких весов! Я люблю тебя и нашу Невероятную семью!»
Конечно, новый набор радости приходит всего через несколько недель после рождения дочери Ника Оникс Айс Коул Пушка с моделью ЛаНиша Коул .
Как мы уже сообщали, Эбби Де Ла Роса , также родит в следующем месяце с их третьим общим ребенком.
К вашему сведению, день рождения Ника тоже в следующем месяце, так что похоже, что в этом сезоне он будет праздновать МНОГО.
Поздравляю.
Снова!!- Бриттани Белл
Ник Кэннон
Телевизор
Дети
дети знаменитостей
Детские часы
Музыка
Еще от ТМЗ
Сан-Диего Падрес Вентилятор бьет кулаками, толкает мужчину вниз по рядам сидений … Во время драки в игре
03. 10.2022 7:40, частьВойна на Украине Российский рэпер покончил с собой… После того, как его призвали на войну, он выступил против
03.10.2022 7:28, частьПоследние новости
Карим Абдул-Джаббар Разрывает Кайри из-за видео Алекса Джонса .
.. Спонсоры должны бросить его!!! 03.10.2022 7:25, частьЭксклюзив
Шон Эйвери из НХЛ Угрожает повредить машину подростка … В жарком споре с соседями
03.10.2022 1:00 PTКим Кардашян Взимается SEC за Crypto Promo Соглашается заплатить 1,26 миллиона долларов
03. 10.2022 6:10, частьЭксклюзив
Тори Ланез Подала в суд беременная женщина, утверждающая, что сбила и сбежала … Он говорит, что это ложь
03.10.2022 7:16, часть«Черная пантера 2»: новый трейлер Летиция Райт стала новым героем … Пост-Чедвик Боузман
03. 10.2022 7:13, частьДК Меткалф Сихокс Тележка вне поля в середине игры … Я должен 💩!!!
03.10.2022, 6:56, частьЭксклюзив
Лиззо Приглашен в кроватку Джеймса Мэдисона… После игры на хрустальной флейте
03. 10.2022, 00:50, частьПиттсбург Стилерс Вентилятор падает с эскалатора… Умирает от травм
03.10.2022 6:00 PTЭксклюзив
Джек Джонсон Фанаты преследуют, преследуют меня… Мне нужна защита, судья!!!
03. 10.2022, 00:30, PTЭксклюзив
Джеффри Дамер Соседская племянница против Мемориала … Шоу причиняет только боль
03.10.2022, 00:20, частьУгадай, кто это Мини-гитарист Превратился в!
03. 10.2022, 00:01, частьЭксклюзивные детали
Марго Робби, Кара Делевинь Помчался на Photog в Аргентине… Друзья спешат на помощь
02.10.2022 13:07, частьЭксклюзивные детали
Комик под огнем Отвечает на шутку Cruise N-Word
9/26/2022 8:25 PTБилли Эйхнер Кажется, виновата гомофобия.
..
Для бомбы кассовых сборов «Братаны» 02.10.2022 16:17, частьЭксклюзив
Ванесса Брайант Посетил концерт Bad Bunny в Лос-Анджелесе… One Gal Pal, охрана на буксире
02.10.2022 16:01, частьЗвезда ‘Till’ Джалин Холл Игра Эммета научила меня этому .
.. Будь собой, будь в курсе 02.10.2022 13:53, частьАдам Левин Выступает с Maroon 5 на мероприятии Shaq’s Fundraiser … Бехати показывает свою поддержку
02.10.2022 9:13:00 по тихоокеанскому времениУилл Смит Отложенный фильм Apple возродили в Вашингтоне.
..
Проверено, хорошая реакция 02.10.2022 12:13, частьDavid Bell
Dakota AllenDaylen BaldwinD’Anthony BellDavid BellJoel BitonioCorey BojorquezJacoby BrissettTaven BryanHarrison BryantJermaine CarterNick ChubbJadeveon ClowneyJack ConklinAmari CooperDawson DeatonGrant DelpitJoshua DobbsMichael DunnJordan ElliottMartin Emerson Jr.Demetric Felton Jr.Tony Fields IIJerome FordMiller ForristallHjalte FroholdtMyles GarrettThomas Graham Jr.Jakeem Grant Sr.A.J. GreenJoe HaegMike Harley Jr.Nick HarrisRonnie Harrison Jr.Brock HoffmanChris HubbardJames Hudson IIICharley HughlettKareem HuntJesse JamesD’Ernest JohnsonJohn Johnson IIIJohn Kelly Jr.Jordan KunaszykRichard LeCounte IIIZaire Mitchell-PadenKellen MondDavid MooreGreg Newsome IIDavid NjokuElijah NkansahChris OdomJeremiah Owusu-KoramoahDonovan Peoples-JonesRoderick Perry IIJacob PhillipsEthan PocicIsaac Рочелл, Честер Роджерс, Джош Розен, Энтони Шварц, Сион Такитаки, Уайатт Теллер, Исайя Томас, Томми Тогиаи, Энтони Уокер-младший, Дензел Уорд, Дешон Уотсон, Стивен Уэтерли, Кертис Уивер, Исайя Уэстон, Тайрон Уитли-младший, Жадный Уильямс, Джедрик Уиллс-младший, Перрион Уинфри, Чейз Винович, Майкл Вудс II, Алекс Райт, Кейд Йорк,
Реклама- РЕЗЮМЕ
- Карьера
- ЖЕЛЕЗНЫЕ
- SPLES
- Ситуационные
Карьера
Первоначально носит из Клевела Браунса в третьем раунде (99 -й).
Ключевые примечания
- Начал 26 из 29 игр за три сезона за Boilermakers с 2019 по 21 год. Завершил студенческую карьеру, сделав 232 улова на 2946 ярдов и 21 приземление.
- Поймал 93 передачи на 1286 ярдов и шесть приемов приземления в 2021 году и был назван первой командой All-Big Ten Conference второй сезон подряд.
- Установил рекорд Пердью, сыграв 17 игр на приеме на 100 ярдов за карьеру, в том числе семь во время его Всеамериканского сезона 2021 года, где он занял второе место по общему количеству приемов за один сезон в школьной истории с 1286.
- Возглавил «Большую десятку» по приемам за игру (8,5) и приему ярдов за игру (116,9) в 2021 году на пути к тому, чтобы быть названным Рихтером-Ховардом Приемником года на конференции.
Личный номер
- Уроженец Индианаполиса, штат Индиана, учился в Центральной средней школе Уоррена.
- Привел свою школьную футбольную и баскетбольную команды к непобежденным сезонам чемпионатов штата. Баскетбольная команда пошла со счетом 32: 0, и он сделал победный бросок, когда истекло время в игре чемпионата.
- Назван игроком года Gatorade 2018 года в Индиане.
- Специалист по финансовому консультированию и планированию в Purdue.
видео
Cleveland Browns Daily — Дэвид Белл присоединяется к шоу в прямом эфире в студии
Новичок Browns WR Дэвид Белл садится за стол вместе с Натаном Зегурой и Бо Бишопом в прямом эфире в студии. Ребята также слышат от главного тренера Кевина Стефански и Джереми Овусу-Корамоа вместе с Майлсом Гарреттом на подиуме.
видео
Дэвид Белл: «Каждый день я прогрессирую».
Ресивер-новичок Дэвид Белл обратился к СМИ 15 июня 2022 года после тренировки команды в Зале славы профессионального футбола. Дэвид рассказывает о своем переходе в НФЛ, о том, над чем он работает, и о своем волнении перед посещением Зала славы профессионального футбола.
видео
Cleveland Browns Daily — округ Колумбия Джо Вудс рассказывает нам о своем состоянии обороны Браунс
Браунс DC Джо Вудс рассказывает Зегуре о полном состоянии защиты Браунов по мере того, как программа межсезонья подходит к концу, а также услышать от ХК Кевина Стефански и WR Дэвид Белл после второй тренировки в мини-лагере!
видео
Cleveland Browns Daily — Дэвид Белл и Алекс Райт присоединяются к шоу
Какой пятничный выпуск программы для вас, детишки! Тренер LB Джейсон Тарвер заходит, чтобы начать шоу, плюс это дебют CBD для новичка WR Дэвида Белла и Эдж Рашера Алекса Райта, поскольку оба выходят один на один с Зегурой в мини-лагере новичков! Все это И мы разбираем расписание Браунов на 2022/23 и расписание НФЛ в целом.
видео
Дэвид Белл: «Мы идем с намерением выиграть хоть одну игру» | Пресс-конференция
Дэвид Белл встречается со СМИ 13 мая 2022 года
видео
Класс драфта новичков
Взгляните на наш класс драфта новичков 2022 года.
видео
Мартин Эмерсон, Алекс Райт и Дэвид Белл | Вводная пресс-конференция
Кливленд Браунс 2022 Выборы третьего раунда драфта выступают перед СМИ 30 апреля 2022 года.
видео
Пресс-конференция Дэвида Белла
Ресивер New Browns Wide Дэвид Белл обращается к СМИ после того, как его выбрали 99-м номером на драфте НФЛ 2022 года.
видео
Дэвид Белл слышит от Эндрю Берри и Кевина Стефански
Дэвид Белл слышит от генерального менеджера Эндрю Берри и главного тренера Кевина Стефански о том, что «Браунс» выбрали его под 99-м номером на драфте НФЛ 2022 года.
новости
«Браунс» ожидают, что Дензел Уорд, Джек Конклин и Дэвид Белл будут готовы к первой неделе
Энтони Уокер-младший и Шелдон Дэй, которые находятся в списке активных/нефутбольных травм, также должны быть готовы к открытию сезона был выбран в третьем раунде драфта НФЛ 2022 года.
Натан Зегура, Джейсон Гиббс и Энтони Пойсал делают свои прогнозы на некоторые из главных вопросов, касающихся Браунов перед тренировочным сбором
новости
Браунс 2022 Предварительный просмотр позиции: Разрушение WR
Амари Купер прибыл, чтобы стать лучшим, и несколько парней будут соревноваться после него за большие роли в игре на пропуск Белл привносит в WR
Лучшая черта Белла — умение ловить мяч, что, по мнению «Браунс», придаст ему большую ценность для нападения в качестве новичка
новости
5 вещей, которые стоит посмотреть в ОТА «Браунс»
The Browns начали OTA во вторник и будут проводить тренировки в течение каждой из следующих трех недель, что приведет к обязательному мини-лагерю
новости
Дэвид Белл готовится к возможной роли в слоте WR
Навыки Белла созрели для слота, где «Браунс» ищут нового игрока, который будет проигрывать каждый
новости
«Браунс» подписали 7 Выборы на драфте 2022 года
«Браунс» подписали семь выборов в своем классе драфта 2022 года с девятью игроками
новости
Тренер Browns WR говорит, что у Browns есть «четкое видение» для новичка Дэвида Белла
Белл, выбранный в третьем раунде 2022 года, проверил многие поля, которые Browns ищут в широком ресивере
новости
Социальные сети реагируют на Browns Day 2 Выборы на драфте
Вот как социальные сети отреагировали на то, что Мартин Эмерсон, Алекс Райт и Дэвид Белл были выбраны в Кливленд0003
новости
Браунс выбрали WR Дэвида Белла под 99-м номером на драфте НФЛ 2022 года
Белл был первой всеамериканской командой в 2021 году
галерея
Вышли фотографии Дэвида Белла, выбранного в третьем раунде «Браунс» в 2022 году.
РекламаЧисла звонков — Academic Kids
From Academic Kids
В комбинаторной математике n th Bell number , названный в честь Эрика Темпла Белла, представляет собой количество разделов набора с n членов. Последовательность номеров Белла начинается следующим образом: Template:OEIS:
Содержимое 1 Перегородки комплекта
2 Другой вид номеров Bell
3 Свойства чисел Белла
4 Наглядный способ расчета чисел Белла
5 См. также
6 Внешние ссылки
Разделы набора
В целом, B n — это количество разделов набора размером n . Раздел множества S определяется как набор непустых, попарно непересекающихся подмножеств S , объединение которых равно S .
Например, B 3 = 5, поскольку набор из трех элементов { a , b , c } можно разделить 5 различными способами:- {{ }, { б }, { с }}
- {{ }, { б , с }}
- {{ б }, { а , в }}
- {{ с }, { а , б }}
- {{ а , б , с }}
B 0 равно 1, потому что в пустом наборе ровно один раздел. Каждый член пустого множества — непустое множество (что совершенно верно), а их объединение — пустое множество. Таким образом, пустой набор является единственным разделом самого себя.
Другой взгляд на числа Белла
Числа Белла также можно рассматривать как количество различных возможных способов положить n помеченных шаров в один или несколько анонимных ящиков. Например, предположим, что n равно 3. У нас есть три шара, которые мы назовем a , b и c , и три коробки.
Если ящики нельзя отличить друг от друга, есть пять способов положить шары в ящики:- Каждый шар идет в свою коробку.
- Все три мяча кладутся в одну коробку. Поскольку ящики анонимны, это считается только одной комбинацией.
- и входит в одну коробку; b и c входят в другой ящик.
- б входит в одну коробку; и и c входят в другую коробку.
- c входит в одну коробку; a и b входят в другую коробку.
Свойства чисел Белла
9n S(n,k).<математика>
2232888949657946267157517765591827437575568527323435768792618847167888789438948060302478614199779726
3678257759505994042279245062445753647863874788822306413960438998857329199453620537788749942016823439
68267785858225339422083619687423225479298171524242007012081418958404496161123201363892701142452
059296721108807672668
73862745341419887853895977737193023441786354602380530218286706381521744667874212992728960187602
026727520376240689650852398468230120896448383085739867131963399875467499177815304267568743
4662852459854922316072421122078373333676860456717485594671823500441075731431468000467316898340014880
0563499537605408024020518232971387570187255225724367813793658229377311514840617597293
· 10 972157574857696235378663027434211359218006858504930450816134076178889687987618389929416815288755835629
± 4.
{n+1/2} \exp\left(n/W(n) — n — 1\вправо)$
предлагает значение 9{O(1)} n$ работают с фиксированной точностью).Сомневаюсь, что этот код можно использовать в реальной жизни, но было весело. упражнение делать. Меня не очень интересуют числа Белла как таковые, а скорее в алгоритмах. Как обычно, взгляд на конкретную проблему помогает понять инструменты, доступные для решения более сложных проблем. В этом случае используются несколько функций Arb:
net |
Индекс блога |
RSS-канал |
Подписывайтесь на меня в Твиттере |
Стать спонсором
Снова!!
10.2022 7:40, часть
.. Спонсоры должны бросить его!!! 03.10.2022 7:25, часть
10.2022 6:10, часть
10.2022 7:13, часть
10.2022, 00:50, часть
10.2022, 00:30, PT
10.2022, 00:01, часть
..
Для бомбы кассовых сборов «Братаны» 02.10.2022 16:17, часть
.. Будь собой, будь в курсе 02.10.2022 13:53, часть
..
Проверено, хорошая реакция 02.10.2022 12:13, часть
Баскетбольная команда пошла со счетом 32: 0, и он сделал победный бросок, когда истекло время в игре чемпионата.
Реклама
Например, B 3 = 5, поскольку набор из трех элементов { a , b , c } можно разделить 5 различными способами:
Если ящики нельзя отличить друг от друга, есть пять способов положить шары в ящики:Число Стирлинга S ( n , k ) — это количество способов разбить множество мощности n ровно на k непустых подмножеств.
n -е число Белла также является суммой коэффициентов полинома, выражающего n -й момент любого распределения вероятностей как функцию первых n кумулянтов; этот способ нумерации разделов не такой грубый, как тот, который дается числами Стирлинга.
9x-1}.<математика>
Наглядный способ расчета чисел Белла
Эту последовательность можно легко рассчитать, выполнив следующие действия:
- Начните с номера один. Поместите это в ряд отдельно.
- Начать новую строку с крайним правым элементом из предыдущей строки в качестве крайнего левого числа
- Определите числа не в левом столбце, взяв сумму числа слева и числа над числом слева (число по диагонали вверх и влево от числа, которое мы вычисляем)
- Повторяйте третий шаг, пока не появится новая строка с числом на одно больше, чем в предыдущей строке
- Номер слева от данной строки Номер звонка для этой строки.
Например, первый ряд создается путем размещения одного элемента отдельно. Следующая (вторая) строка получается путем взятия самого правого числа из предыдущей строки (1) и помещения его в новую строку. Теперь у нас есть такая структура:
1 1 х
Значение x здесь определяется путем сложения числа слева от x (один) и числа над числом слева от x (тоже один).
