Фигура трапеция: Трапеция — что это такое, свойства и виды трапеций (равнобедренная, прямоугольная)

Содержание

Трапеция — что это такое, свойства и виды трапеций (равнобедренная, прямоугольная)

Обновлено 22 июля 2021

Определение
Происхождения слова
Стороны трапеции
Равнобедренная и прямоугольная
Свойства трапеций

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. В этой статье мы решили подробно рассказать о такой геометрической фигуре, как ТРАПЕЦИЯ.

Ее подробно изучают на уроках геометрии в 8-м классе. И эти уроки являются частью общего знакомства школьников с различными четырехугольниками.

Определение трапеции

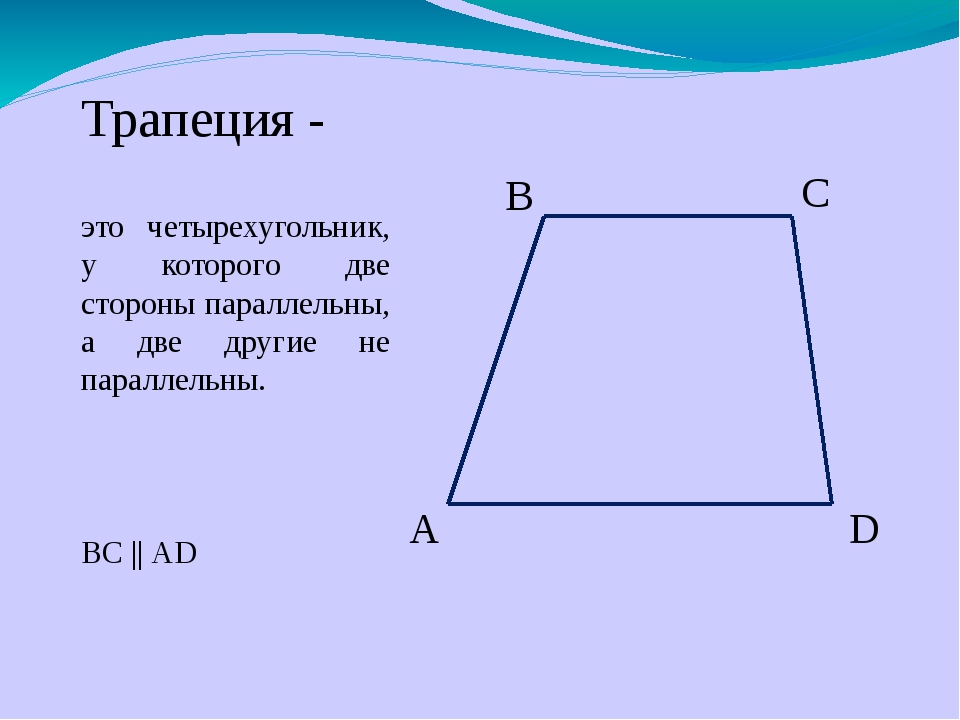
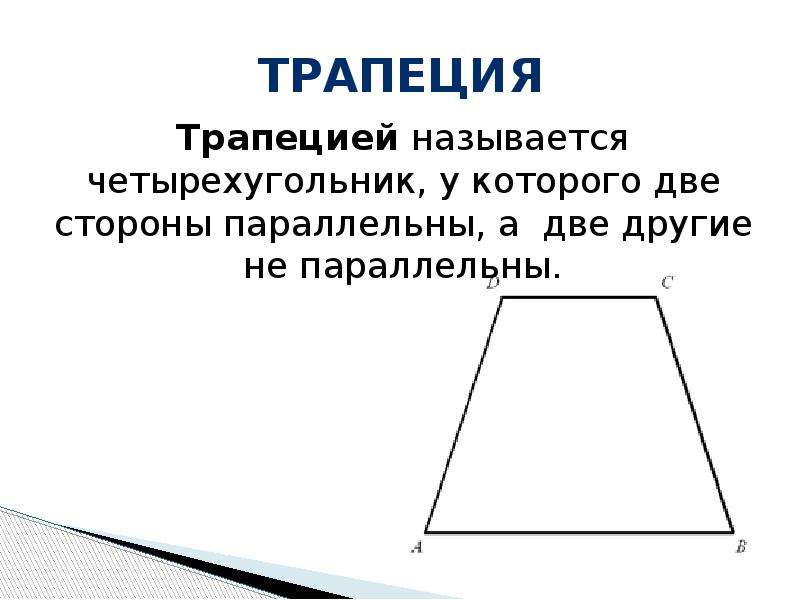
Трапеция – геометрическая фигура, которая представляет собой четырехугольник, у которого две противоположные стороны располагаются на параллельных прямых. А две другие стороны должны, наоборот, быть не параллельными.

Вот так выглядит классическая трапеция:

У этой фигуры стороны АВ и CD являются параллельными. А вот AD и CB – нет.

Происхождения слова

Первое упоминание об этой фигуре встречается еще в трудах известного древнегреческого математика Евклида.

В его книге «Начала» этим термином описывается абсолютно любой четырехугольник, который не является параллелограммом.

Если кто не помнит, параллелограммом называют четырехугольник, у которого противоположные стороны параллельны. Выглядит эта фигура в классическом понимании вот так:

Интересно, что и всем известные фигуры – квадрат, прямоугольник (что это?) и ромб (это как?) – также являются частным случаем параллелограмма. Ведь действительно – у них противоположные стороны параллельны друг к другу.

И получается, что Евклид был в целом прав. Он просто поделил все четырехугольники на две большие категории – параллелограммы и трапеции.

Кстати, само слово ТРАПЕЦИЯ также имеет греческое происхождение. В древние времена оно звучало как «трапедзион». И в переводе это означает «обеденный стол». Поэтому слово «трапеза», которое у нас является синонимом любого приема пищи тоже родом оттуда.

Стороны трапеции

Парные стороны трапеций имеют свои названия:

Основания трапеции – стороны, которые располагаются на параллельных прямых.
Боковые – стороны, которые не находятся на параллельных прямых.

Закрепим это с помощью рисунка:

В данном случае стороны АВ и CD параллельны друг другу. А значит, именно они являются основаниями. А вот АС и BD – наоборот, явно не параллельны. И соответственно, это боковые стороны.

Кстати, расположение сторон не зависит от расположения самой фигуры. Даже вот в таких положениях

все равно параллельные стороны будут считаться основаниями, а непараллельные – боковыми.

Равнобедренная и прямоугольная трапеции

Вариант трапеции, который мы рассмотрели – это самые распространенные виды геометрической фигуры. Но есть и частные случаи:

Равнобедренная трапеция – та, у которой боковые (не параллельные) стороны равны. Ее еще называют равнобокой или равнобочной.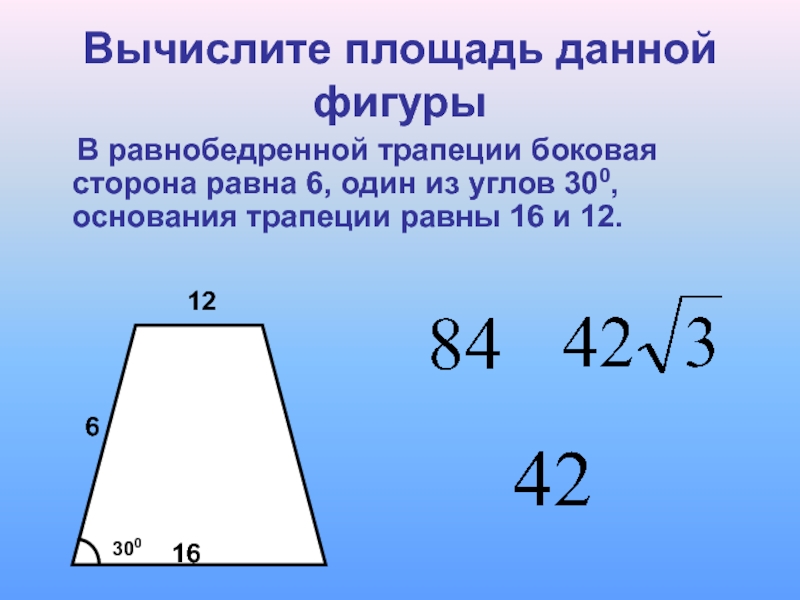

Выглядит она вот так:

В данном примере графически показано, что стороны AD и ВС равны между собой. Об этом свидетельствуют небольшие черточки.

Прямоугольная трапеция – та, у которой одна из боковых сторон и основания образовывают прямой угол.

Выглядит она вот так:

В данном примере, углы DAB и ADC являются прямыми, то есть равны 90 градусам. А соответственно, трапеция называется прямоугольной.

Тут важно заметить, что под прямым углом к основанию должна идти только одна боковая сторона. Если будут обе, то трапеция автоматически превратится в квадрат.

Свойства трапеций

С трапециями связаны несколько понятий в геометрии, которые активно используются для решения различных теорем.

Средняя линия

Средняя линия трапеции – это отрезок, который идет параллельно основаниям и соединяет середины:

Со средней линией связана одна интересная теорема. Очень часто на уроках геометрии школьников просят определить ее длину. И сделать это весьма просто.

Длина средней линии трапеции равна половине суммы длин ее оснований.

Звучит может и несколько тяжеловато. Но на деле – это весьма просто. Так, чтобы посчитать в нашем примере длину отрезка MN, который является средней линией, надо применить формулу:

MN = (AD + ВС) / 2

И это правило распространяется на все виды трапеций.

Биссектриса углов трапеции

Биссектриса – это линия (луч), которая делит угол пополам. Так вот

Любая биссектриса, выведенная из угла трапеции, отсекает на основании отрезок, равный по длине боковой стороне.

На данном рисунке отрезок АЕ является биссектрисой угла ABD. И исходя из этого, отрезки АВ и ВЕ равны между собой, о чем свидетельствуют небольшие черточки на них.
В то же время у биссектрис в трапеции есть еще одно свойство.

Две биссектрисы, выведенные из углов одной боковой стороны, пересекаются под прямым углом.

Все эти теоремы в процессе школьного обучения, ученикам еще необходимо доказывать. Ну а мы решили не приводить долгие математические и геометрические выкладки. Просто примите как данность!

Вот и все, что мы хотели рассказать вам о трапеции.

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Эта статья относится к рубрикам:

Геометрическая фигура трапеция. Виды трапеций. Свойства равнобедренной трапеции

1. ТРАПЕЦИЯ

2. Определение Трапецией называют четырехугольник, у которого две стороны параллельны, а две другие не параллельны.

Трапеция
от греч. trapeza — стол.
Трапеция буквально — «столик».
Геометрическая фигура была названа
так по внешнему сходству с маленьким
столом.

5. Элементы трапеции

Основание
Боковая
сторона
B
А
Основание
AD, BC – основания,
AB, CD – боковые стороны
C
D
Боковая
сторона

6. Определение Высотой трапеции называют перпендикуляр, опущенный из любой точки прямой, содержащей одно из оснований, на прямую,

содержащую другое
основание.

7. Виды трапеций

прямоугольная
равнобедренная
Трапецию, у которой боковые стороны равны,
называют равнобедренной.
Трапецию, у которой боковая сторона является её
высотой, называют прямоугольной.

8. Свойства равнобедренной трапеции

B
C
А
B
D
1) Углы при основаниях равны
A= B
C
А
D
2) Диагонали равны AC=BD

9. Признаки равнобедренной трапеции

B
А
C
B
D
1) Если углы при основании
трапеции равны, то трапеция
равнобедренная
Если A= B,
то ABCD – равнобедренная
трапеция
C
А
D
2) Если диагонали трапеции
равны, то трапеция
равнобедренная
Если AC=BD,
то ABCD – равнобедренная
трапеция

10.

Средняя линия трапеции A
М
Средняя линия трапеции –
отрезок, соединяющий
середины боковых сторон
B
N
MN– средняя линия
C
Средняя линия трапеции равна полусумме её оснований
MN=½(AB+DC)
Являются ли четырёхугольники трапециями?
В
1.
2.
90°
А 90°
N
100°
С
E
D
3.
C
60°
F
M
4.
80°
K
K
130°
E
P
60°
D
82°
98°
H
R

Трапеция

\[{\Large{\text{Произвольная трапеция}}}\]

Определения

Трапеция – это выпуклый четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.

Параллельные стороны трапеции называются её основаниями, а две другие стороны – боковыми сторонами.

Высота трапеции – это перпендикуляр, опущенный из любой точки одного основания к другому основанию.

Теоремы: свойства трапеции

1) Сумма углов при боковой стороне равна $180^\circ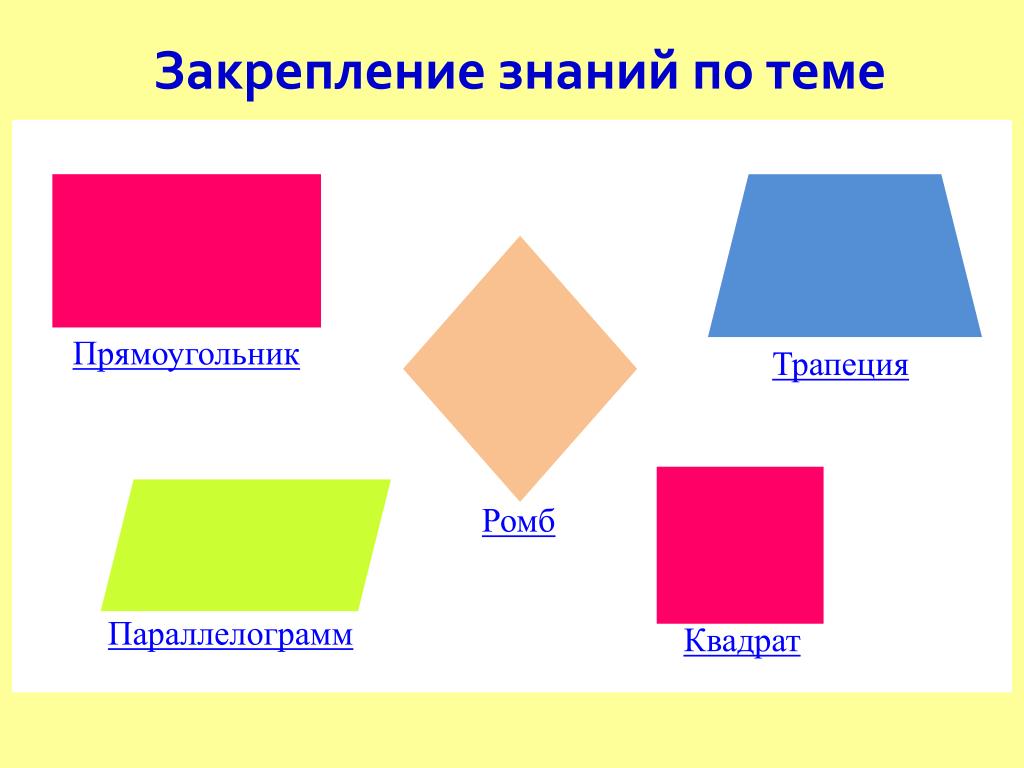$. \circ\).

2) Т.к. $AD\parallel BC$ и $BD$ – секущая, то $\angle DBC=\angle BDA$ как накрест лежащие.
Также $\angle BOC=\angle AOD$ как вертикальные.
Следовательно, по двум углам $\triangle BOC \sim \triangle AOD$.

Докажем, что $S_{\triangle AOB}=S_{\triangle COD}$. Пусть $h$ – высота трапеции. Тогда $S_{\triangle ABD}=\frac12\cdot h\cdot AD=S_{\triangle ACD}$. Тогда: \[S_{\triangle AOB}=S_{\triangle ABD}-S_{\triangle AOD}=S_{\triangle ACD}-S_{\triangle AOD}=S_{\triangle COD}\]

Определение

Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.

Теорема

Средняя линия трапеции параллельна основаниям и равна их полусумме.

Доказательство*
С доказательством рекомендуется ознакомиться после изучения темы “Подобие треугольников”.

1) Докажем параллельность.

Проведем через точку $M$ прямую $MN’\parallel AD$ ($N’\in CD$). Тогда по теореме Фалеса (т.к. $MN’\parallel AD\parallel BC, AM=MB$) точка $N’$ — середина отрезка $CD$. Значит, точки $N$ и $N’$ совпадут.

2) Докажем формулу.

Проведем $BB’\perp AD, CC’\perp AD$. Пусть $BB’\cap MN=M’, CC’\cap MN=N’$.

Тогда по теореме Фалеса $M’$ и $N’$ — середины отрезков $BB’$ и $CC’$ соответственно. Значит, $MM’$ – средняя линия $\triangle ABB’$, $NN’$ — средняя линия $\triangle DCC’$. Поэтому: \[MM’=\dfrac12 AB’, \quad NN’=\dfrac12 DC’\]

Т.к. $MN\parallel AD\parallel BC$ и $BB’, CC’\perp AD$, то $B’M’N’C’$ и $BM’N’C$ – прямоугольники. По теореме Фалеса из $MN\parallel AD$ и $AM=MB$ следует, что $B’M’=M’B$. Значит, $B’M’N’C’$ и $BM’N’C$ – равные прямоугольники, следовательно, $M’N’=B’C’=BC$.

Таким образом:

\[MN=MM’+M’N’+N’N=\dfrac12 AB’+B’C’+\dfrac12 C’D=\] \[=\dfrac12 \left(AB’+B’C’+BC+C’D\right)=\dfrac12\left(AD+BC\right)\]

Теорема: свойство произвольной трапеции

Середины оснований, точка пересечения диагоналей трапеции и точка пересечения продолжений боковых сторон лежат на одной прямой.

1) Докажем, что точки $P$, $N$ и $M$ лежат на одной прямой.

Проведем прямую $PN$ ($P$ – точка пересечения продолжений боковых сторон, $N$ – середина $BC$). Пусть она пересечет сторону $AD$ в точке $M$. Докажем, что $M$ – середина $AD$.

Рассмотрим $\triangle BPN$ и $\triangle APM$. Они подобны по двум углам ($\angle APM$ – общий, $\angle PAM=\angle PBN$ как соответственные при $AD\parallel BC$ и $AB$ секущей). Значит: \[\dfrac{BN}{AM}=\dfrac{PN}{PM}\]

Рассмотрим $\triangle CPN$ и $\triangle DPM$. Они подобны по двум углам ($\angle DPM$ – общий, $\angle PDM=\angle PCN$ как соответственные при $AD\parallel BC$ и $CD$ секущей). Значит: \[\dfrac{CN}{DM}=\dfrac{PN}{PM}\]

Отсюда $\dfrac{BN}{AM}=\dfrac{CN}{DM}$. Но $BN=NC$, следовательно, $AM=DM$.

2) Докажем, что точки $N, O, M$ лежат на одной прямой.

Пусть $N$ – середина $BC$, $O$ – точка пересечения диагоналей. Проведем прямую $NO$, она пересечет сторону $AD$ в точке $M$. Докажем, что $M$ – середина $AD$.

$\triangle BNO\sim \triangle DMO$ по двум углам ($\angle OBN=\angle ODM$ как накрест лежащие при $BC\parallel AD$ и $BD$ секущей; $\angle BON=\angle DOM$ как вертикальные). Значит: \[\dfrac{BN}{MD}=\dfrac{ON}{OM}\]

Аналогично $\triangle CON\sim \triangle AOM$. Значит: \[\dfrac{CN}{MA}=\dfrac{ON}{OM}\]

Отсюда $\dfrac{BN}{MD}=\dfrac{CN}{MA}$. Но $BN=CN$, следовательно, $AM=MD$.

\[{\Large{\text{Равнобедренная трапеция}}}\]

Определения

Трапеция называется прямоугольной, если один из ее углов – прямой.

Трапеция называется равнобедренной, если ее боковые стороны равны.

Теоремы: свойства равнобедренной трапеции

1) У равнобедренной трапеции углы при основании равны.

2) Диагонали равнобедренной трапеции равны.

3) Два треугольника, образованные диагоналями и основанием, являются равнобедренными.

Доказательство

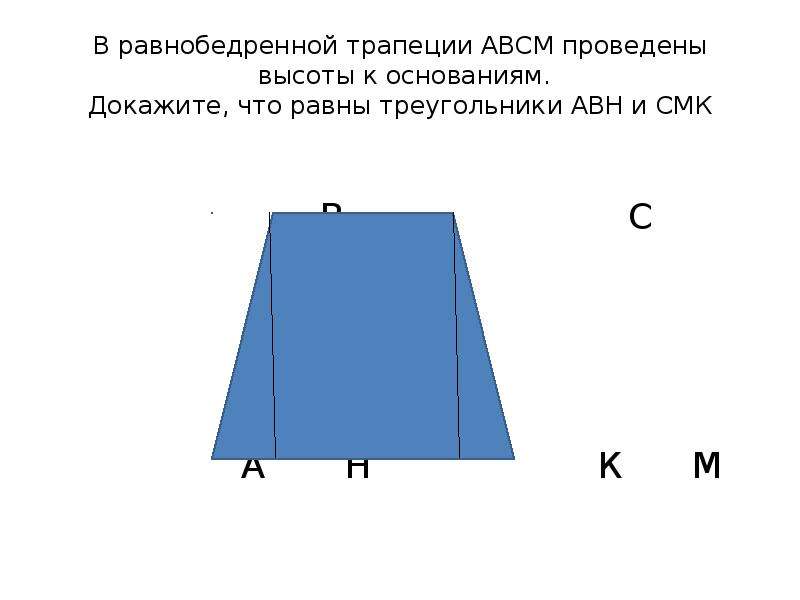
1) Рассмотрим равнобедренную трапецию $ABCD$.

Из вершин $B$ и $C$ опустим на сторону $AD$ перпендикуляры $BM$ и $CN$ соответственно. Так как $BM\perp AD$ и $CN\perp AD$, то $BM\parallel CN$; $AD\parallel BC$, тогда $MBCN$ – параллелограмм, следовательно, $BM = CN$.

Рассмотрим прямоугольные треугольники $ABM$ и $CDN$. Так как у них равны гипотенузы и катет $BM$ равен катету $CN$, то эти треугольники равны, следовательно, $\angle DAB = \angle CDA$.

Т.к. $AB=CD, \angle A=\angle D, AD$ – общая, то по первому признаку $\triangle ABD=\triangle ACD$. Следовательно, $AC=BD$.

3) Т.к. $\triangle ABD=\triangle ACD$, то $\angle BDA=\angle CAD$. Следовательно, треугольник $\triangle AOD$ – равнобедренный.

Аналогично доказывается, что и $\triangle BOC$ – равнобедренный.

Теоремы: признаки равнобедренной трапеции

1) Если у трапеции углы при основании равны, то она равнобедренная.

2) Если у трапеции диагонали равны, то она равнобедренная.

Доказательство

Рассмотрим трапецию $ABCD$, такую что $\angle A = \angle D$.

Достроим трапецию до треугольника $AED$ как показано на рисунке. Так как $\angle 1 = \angle 2$, то треугольник $AED$ равнобедренный и $AE = ED$. Углы $1$ и $3$ равны как соответственные при параллельных прямых $AD$ и $BC$ и секущей $AB$. Аналогично равны углы $2$ и $4$, но $\angle 1 = \angle 2$, тогда $\angle 3 = \angle 1 = \angle 2 = \angle 4$, следовательно, треугольник $BEC$ тоже равнобедренный и $BE = EC$.

В итоге $AB = AE — BE = DE — CE = CD$, то есть $AB = CD$, что и требовалось доказать.

2) Пусть $AC=BD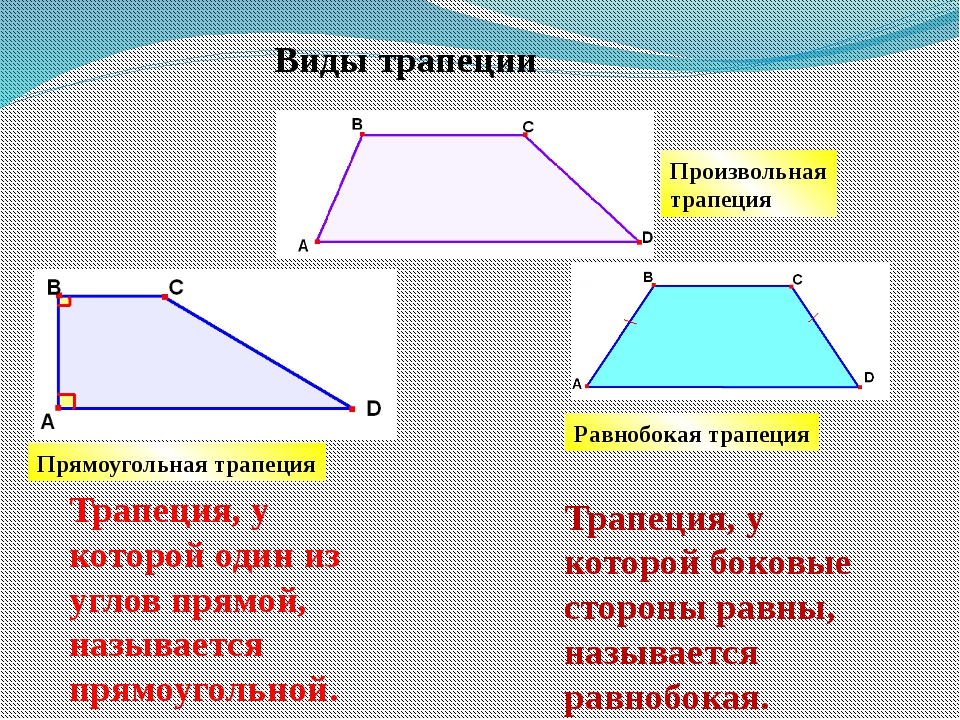$. Т.к. $\triangle AOD\sim \triangle BOC$, то обозначим их коэффициент подобия за $k$. Тогда если $BO=x$, то $OD=kx$. Аналогично $CO=y \Rightarrow AO=ky$.

Т.к. $AC=BD$, то $x+kx=y+ky \Rightarrow x=y$. Значит $\triangle AOD$ – равнобедренный и $\angle OAD=\angle ODA$.

Таким образом, по первому признаку $\triangle ABD=\triangle ACD$ ($AC=BD, \angle OAD=\angle ODA, AD$ – общая). Значит, $AB=CD$, чтд.

Трапеция — это… Что такое Трапеция?

Трапе́ция (от др.-греч. τραπέζιον — «столик»; τράπεζα — «стол, еда») — четырёхугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна). Две параллельные стороны называются основанием трапеции, а две другие — это боковые стороны. Иногда трапеция определяется как четырёхугольник, у которого пара противолежащих сторон параллельна (про другую не уточняется), в этом случае параллелограмм является частным случаем трапеции.

В частности, существует понятие криволинейная трапеция.

Связанные определения

Элементы трапеции

Параллельные стороны называются основаниями трапеции.
Две другие стороны называются боковыми сторонами.
Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.
Расстояние между основаниями называется высотой трапеции.

Виды трапеций

Прямоугольная трапеция Равнобедренная трапеция

Трапеция, у которой боковые стороны равны, называется равнобокой или равнобедренной.
Трапеция, имеющая прямые углы при боковой стороне, называется прямоугольной.

Общие свойства

Средняя линия трапеции параллельна основаниям и равна их полусумме.

Отрезок, соединяющий середины диагоналей, равен полуразности оснований.
(Обобщённая теорема Фалеса). Параллельные прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки.
В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.

Свойства и признаки равнобедренной трапеции

Прямая, проходящая через середины оснований, перпендикулярна основаниям и является осью симметрии трапеции.
Высота, опущенная из вершины на большее основание, делит его на два отрезка, один из которых равен полусумме оснований, другой — полуразности оснований.
В равнобедренной трапеции углы при любом основании равны.
В равнобедренной трапеции длины диагоналей равны.
Если трапецию можно вписать в окружность, то она равнобедренная.
Около равнобедренной трапеции можно описать окружность.

Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.

Вписанная и описанная окружность

Площадь

Здесь приведены формулы, свойственные именно трапеции. См. также формулы для площади произвольных четырёхугольников.

В случае, если и — основания и — высота, формула площади:

В случае, если — средняя линия и — высота, формула площади:

ɴʙ Эти формулы — одинаковы, так как полусумма оснований равняется средней линии трапеции:

Формула, где , — основания, и — боковые стороны трапеции:

Площадь равнобедренной трапеции с радиусом вписанной окружности, равным , и углом при основании :

В частности, если угол при основании равен 30°, то:

См. также

Примечания

Тип фигуры — груша или трапеция

Тип фигуры трапеция или, проще говоря, груша. Это довольно часто встречающийся тип женской фигуры.

Основные признаки:

Объем бедер и объем талии имеет явно выраженную разницу
Полные округлые бедра
Узкие плечи
Плоский живот
Тонкая длинная шея
Небольшая грудь

Jennifer Lopez	Nicole Scherzinger

Natalia Oreiro

Представительницы такого типа фигуры часто сталкиваются с проблемой как зрительно уменьшить бедра. Главное правило при таком телосложение – это уравновесить ширину бедер с плечами. При помощи одежды этого вполне можно достичь!

Во-первых, для женщин с типом фигуры груша необходимо зрительно увеличить плечи. Широкие плечи сбалансируют широкие бедра. При этом подчеркивайте талию при помощи поясов, ремней, приталенной одежды.

Во-вторых, носите более темные цвета, вертикальные линии и матовую ткань в нижней части тела.


Ermanno Scervino	Dolce & Gabbana

На фото справа объемная линия плеч. Слева – горизонтальный рисунок в области груди, делающий эту часть шире.


Dolce & Gabbana	Dolce & Gabbana

Диагональные полосы в форме конуса вершиной вверх создают сильный эффект уменьшения объема.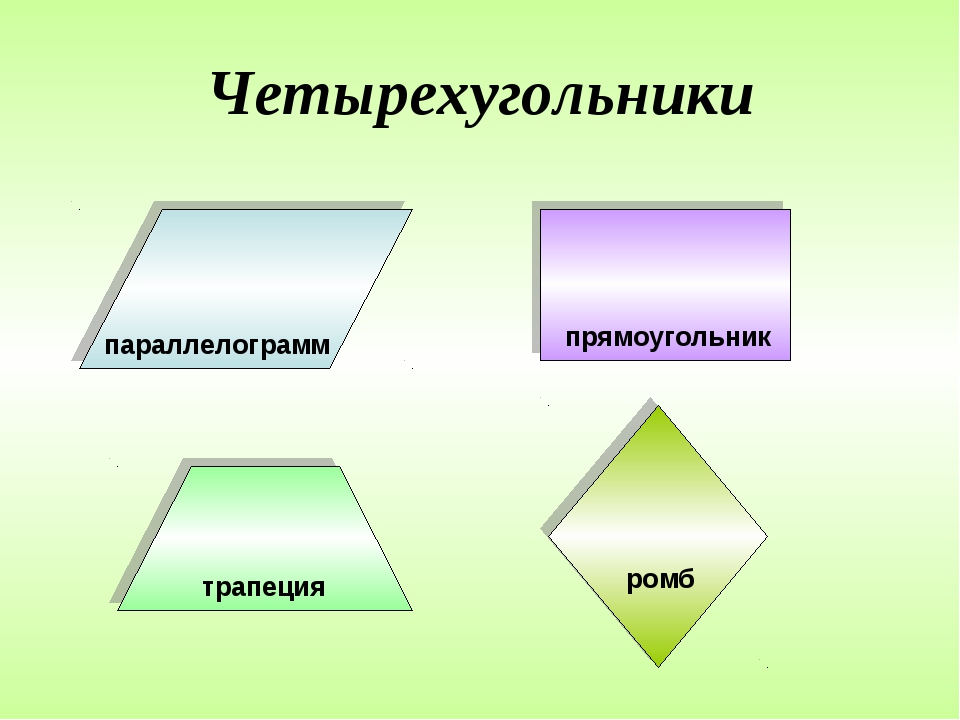

На фото справа юбка из матовой грубоватой ткани, способствующей скрыть объем бедра.


Dolce & Gabbana	Dolce & Gabbana

Контрастные вертикальные линии удлиняют силуэт на фото справа. Слева – набивные цветы гипюра придают дополнительный объем.

А теперь детально о гардеробе для типа фигуры — груша.

Носите платья и юбки длиной от середины колена и ниже. Силуэт должен быть слегка зауженный или слегка расклешенный от бедра.

Наиучший стиль для этого типа женской фигуры – ампир. Платья в этом стиле плотно прилегают по лифу и плавно струятся по бедрам.

Всегда носите плечики, полуприталенные и присборенные верхние части, чтобы подчеркнуть талию. Например, блузки и платья с запахом.

Чтобы зрительно увеличить плечи, выбирайте крупные воротники блузок, максимальную деталировку и декор в области плеч и груди такие, как вырез «лодочка», рукав «фонарик», платок или шарф, уложенный на плечи.

Обувь носить желательно на низком каблуке и с открытым вырезом. В холодное время года старайтесь, чтобы юбка, колготы и обувь были в одном цвете. Таким образом, получается одна сплошная вертикаль от талии до носка, что удлиняет силуэт.


Jennifer Aniston	Ксения Сухинова

И еще. Всегда выбирайте сумки на ремне выше бедер или клатч. Такие аксессуары не будут акцентировать те места, которые хотелось бы скрыть.


Eva Mendes	Nicole Richie, Chanel

Тип женской фигуры груша воплощает собой женственность. Не стесняйтесь, если природа наградила Вас широкими бедрами. Учитесь правильно их корректировать одеждой, и тогда округлые бедра станут Вашим достоинством.

Дополнительная информация

О типе фигуры песочные часы

О типе фигуры перевернутый треугольник

Гардероб по типу фигуры: фото и рекомендации

Одежда для типа фигуры:

Мало кого из женщин нашей планеты природа наградила сразу и ногами «от ушей», и осиной талией, и грудью 5-того размера. Как же быть тем, кто мечтает выглядеть по-королевски, а внешние данные до идеальных явно не дотягивают?

Шикарная фигура на самом деле — не такой уж и неотъемлемый признак «женщины-королевы», гораздо важнее уметь скрыть свои недостатки и подчеркнуть имеющиеся достоинства. Сделать это можно с помощью правильно подобранной одежды. Прежде чем отправляться за обновками в магазин, определите, к какому типу телосложения относится ваша фигура. Итак, выбираем гардероб по типу фигуры.

Все фигуры условно разделяют на 4 типа: трапеция (груша), треугольник, прямоугольник и песочные часы. Иногда добавляют яблоко (округлый вариант прямоугольника).

Одежда для женщин с типом фигуры трапеция (груша)

У женщины с фигурой-трапецией обычно четкая талия и бедра шире плеч. С такой фигурой ни в коем случае нельзя носить облегающие вещи, лучше всего в этом случае будет смотреться полуприлегающая одежда.

Если у вас красивые ноги, очень хорошо подойдут вам слегка расширяющиеся к подолу юбки или брюки, скроенные прямо и зауженные внизу. Такие вещи отвлекут внимание от излишне широких бедер и, наоборот, притянут взгляды к стройным ножкам.

Зрительно уменьшить бедра поможет и выбор цвета одежды.

Если мы выбираем гардероб по типу фигуры «трапеция», стоит отдавать предпочтение темным черным или коричневым оттенкам брюк, джинсов и юбок и однотонным пастельным – блузок, свитеров и кофточек. Выбирая платье, стоит остановиться на том варианте, который выгодно подчеркнет грудь.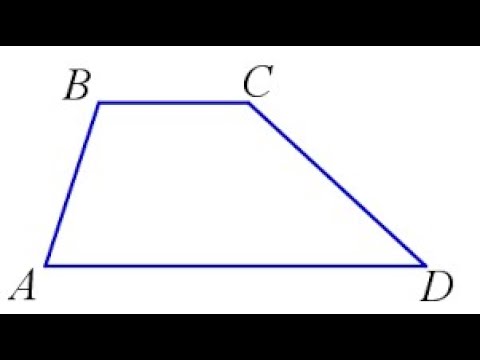

Слегка приталенное платье светло-зеленого, белого, голубого или сиреневого цветов придаст вашей фигуре практически идеальные пропорции.

Хороши для «груш» такие фасоны:

— платье с полуприлегающим верхом и юбкой-солнце или полусолнце длиной до середины колена;
— двухцветное платье с небольшой баской: верх светлый, низ темный;
— юбка-«рыбка» (приталенная, плотно обхватывающая бедра и мягко спускающаяся, расширяясь, до середины икры).

Женственным «грушам» стоит также обратить внимание на юбку-шорты. Эта модель настолько универсальна, что не только скроет лишние объемы «внизу», но и сделает ваш образ еще более притягательным за счет некоторой загадочности, неопределенности (не то юбка, не то шорты…).

Красиво смотрятся на «грушах» платья-футляры, платья с глубоким и широким вырезом, с пышным коротким рукавчиком. Вообще, «груши», помните: разнообразные платья – это ваш правильный выбор! А брюк и джинсов пусть будет немного поменьше в гардеробе.

Одежда для женщин с типом фигуры «перевернутый треугольник»

У фигуры-треугольника плечи, наоборот, шире бедер. Ее обладательницам стоит подчеркивать линию талии и делать акцент на красивых бедрах.

Придется отказаться от крупных орнаментов и рисунков, а также от горизонтальных полос на кофтах, джемперах и блузках.

Жакеты лучше выбирать приталенные, с большими карманами и V-вырезом.
Брюки и джинсы, в общем, подойдут любые. На такой фигуре будут выигрышно смотреться как раз светлые джинсы, особенно в сочетании с рубашками того же оттенка.
Также светлыми должны быть и юбки, хорошо, если ткань будет в клетку или косую полоску. Длина юбок для «женщин-треугольников» может быть любая – чем краше ножки, тем короче юбка (естественно, в разумных пределах).
«Треугольники» словно созданы для однотонных прямых платьев простого покроя. Лучше всего выбирать укороченные модели.
Юбка-карандаш, которая хороша для любого возраста, способна придать шарм и элегантность даме с фигурой «перевернутый треугольник». Только нужно сбалансировать пропорции: например, выбрать юбку с накладными карманами или каким-нибудь ярким узором.

Как ни странно, модные сегодня платья с обтягивающим верхом и пышной-юбкой-«солнце» пойдут «треугольнику» не меньше, чем «груше». Но в данном случае верх должен быть именно четко облегающим фигуру. Кроме того, идеальный ворот для такого платья – закрытый. Хороши разнообразные воротнички-стойки, маленькие светлые воротнички «а ля гимназистка».

Прекрасно смотрятся на «треугольниках» платья-рубашки с тонким пояском.

Одежда для женщин с типом фигуры «Прямоугольник»

Женщины с фигурой-прямоугольником, как правило, имеют пропорциональные бедра и плечи при нечетко выраженной талии. Очень важно в таком случае для придания стройности очертить линию талии. Для этого стоит отдать предпочтение юбкам без пояса, брюкам-капри, жакетам прямого покроя и блузкам с небольшим рукавом.

Очень красиво на такой фигуре смотрятся платья на бретельках с прямым вырезом.

Когда выбираем гардероб по типу фигуры «прямоугольник», цвета в одежде можно в принципе использовать любые с условием, что и верх, и низ будут одного тона.

Аксессуары в виде разнообразных ремней лучше вообще исключить, они только подчеркнут недостатки, никак их не скрыв. Исключением может послужить широкий ремень контрастного цвета, не слишком плотно обхватывающий талию. Его роль в данном случае – «разделить» зрительно фигуру, «создать» линию талии, даже если фактически ее почти нет.

На ножках будет красиво смотреться обувь на невысоком каблуке или на платформе.

Хорошо сидят на «прямоугольниках» укороченные пиджаки, «косухи», джинсовые курточки.

Узкие джинсы и брюки смотрятся на такой фигурке гораздо лучше, чем на любой другой. Если вы обладаете такой фигурой, то можете смело позволить себе:

— брюки скинни и топ с круглым вырезом;
— леггинсы и свободный свитер;
— ультракороткие шортики со свободной клетчатой блузкой.

«Мальчишеская» фигура дает возможность спокойно носить балетки (благодаря тому, что ноги у таких девушек обычно длинные и стройные, балетки не придадут образу тяжеловесность) или сапоги без каблука.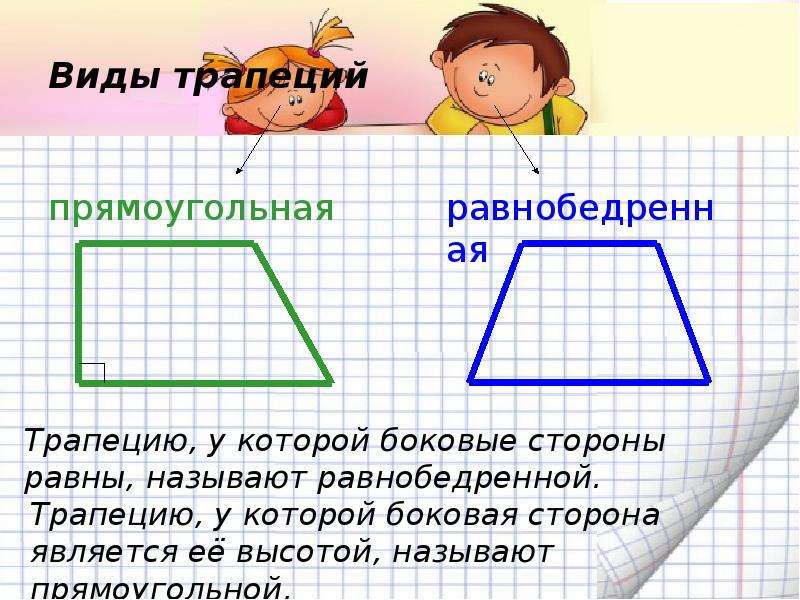

На холодное время года женщины с такой фигурой могут приобрести пальто в стиле «оверсайз» (то есть объемное) или полупальто длиной до бедер. Пиджачный крой будет просто великолепен в данном случае.

Одежда для типа фигуры «Яблоко»

«Яблоко» — в принципе, это одна из вариаций «прямоугольника». Женщины-«яблочки» тоже отличаются стройными ногами, прямыми плечами. Талия не выражена, присутствует лишь намек на нее. При этом они часто имеют полноватую грудь, слегка выдающийся животик, круглое лицо. Как одеться «яблоку»?

Сразу – о важном: детали, привлекающие внимание, сконцентрируйте наверху. Пусть это будут:

— яркий шарфик;
— крупная брошь;
— красивые бусы.

Талию не акцентируем. Но можно использовать в некоторых моделях широкий жесткий пояс. Платья нужно подбирать полуприлегающие, желательно с рукавом. Хороши платья с запахом, с мягкими складочками в районе живота. Если вы решили надеть топ – пусть он будет снабжен квадратным декольте или каким-либо другим вырезом необычной, притягивающей взгляд формы.

«Яблоку» со стройными ногами не возбраняется мини. Интересно, что короткие юбки и шорты «сидят» на такой фигуре отлично почти в любом возрасте.

Хороши свободные брюки из мягких тканей. Выбираете купальник? Обратите внимание на танкини или цельный с вертикальными узорами.

Одежда для женщин с типом фигуры «Песочные часы»

Женщинам с фигурой «песочные часы» повезло больше всех – им пойдет любая одежда, лишь бы она не была бесформенной и безразмерной.

Брюки или джинсы лучше выбирать с заниженной талией, такие будут смотреться более выигрышно чем, к примеру, широкие брюки с высокой посадкой. Хотя и широкие брюки могут выглядеть на женщине-«песочных часах» очень эффектно, если надеть их, например, с белой блузкой и черным корсетом.

Дополнить образ можно любыми аксессуарами, бижутерией, высокими каблуками – позволяется практически все. Однако увлекаться тоже не стоит, красивая фигура – еще не повод навешивать на себя все доступные украшения.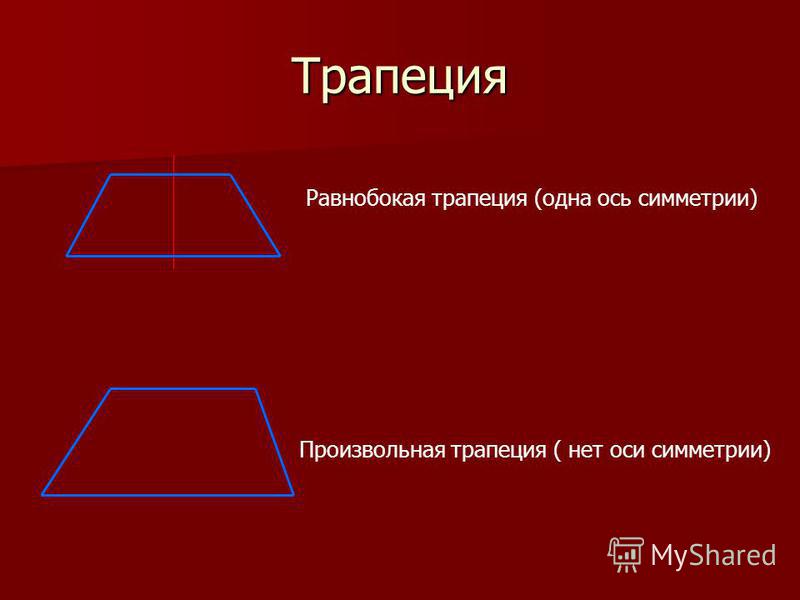

Фигура «песочные часы» дает возможность экспериментировать. Кому-то больше пойдет маленькое черное платье «в облипку»; кто-то будет увереннее себя чувствовать в классическом офисном костюме; кто-то выберет ретро-стиль, а кого-то прельщает эпатажный стиль трэш.

Для «песочных часов» строгих запретов нет. Нужно ориентироваться главным образом на возраст, образ жизни и собственные предпочтения.

Природа наделила нас разными фигурами. Но каждая – прекрасна. Надо лишь научиться подчеркивать достоинства.

]]>

Трапеция. Свойства, признаки трапеции | Подготовка к ЕГЭ по математике

Трапеция – четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна).

Параллельные стороны трапеции называются основаниями. Другие две — боковые стороны.
Если боковые стороны равны, трапеция называется равнобедренной.

Трапеция, у которой есть прямые углы при боковой стороне, называется прямоугольной.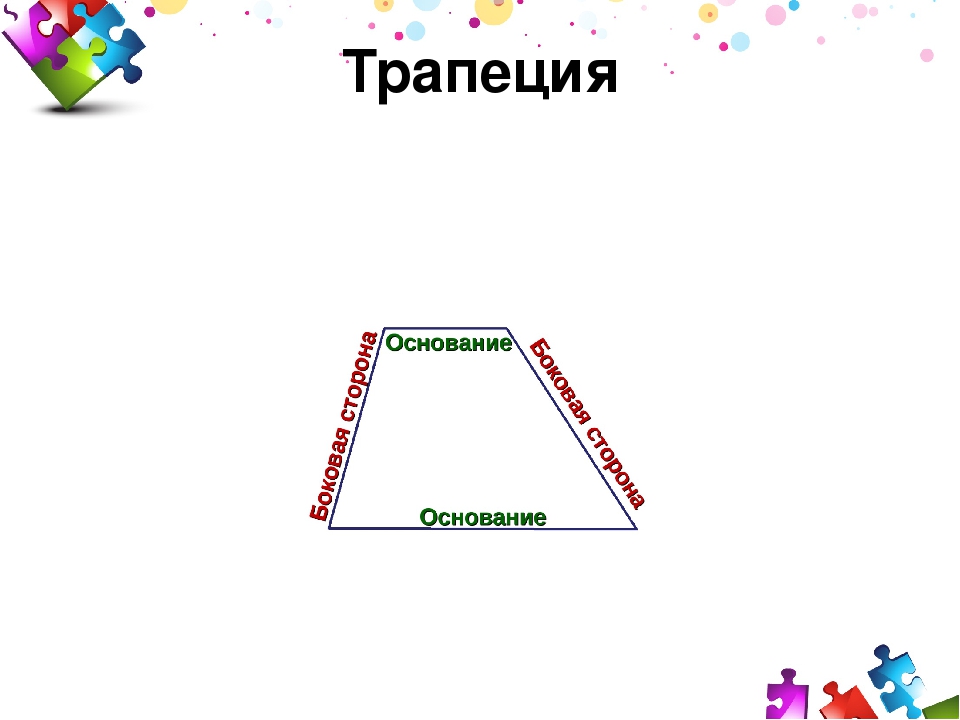

Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.

Свойства трапеции

1. Средняя линия трапеции параллельна основаниям и равна их полусумме.

2. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.

3. Треугольники и , образованные отрезками диагоналей и основаниями трапеции, подобны.

Коэффициент подобия –

Отношение площадей этих треугольников есть .

4. Треугольники и , образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь.

5. В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.

6. Отрезок, соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии.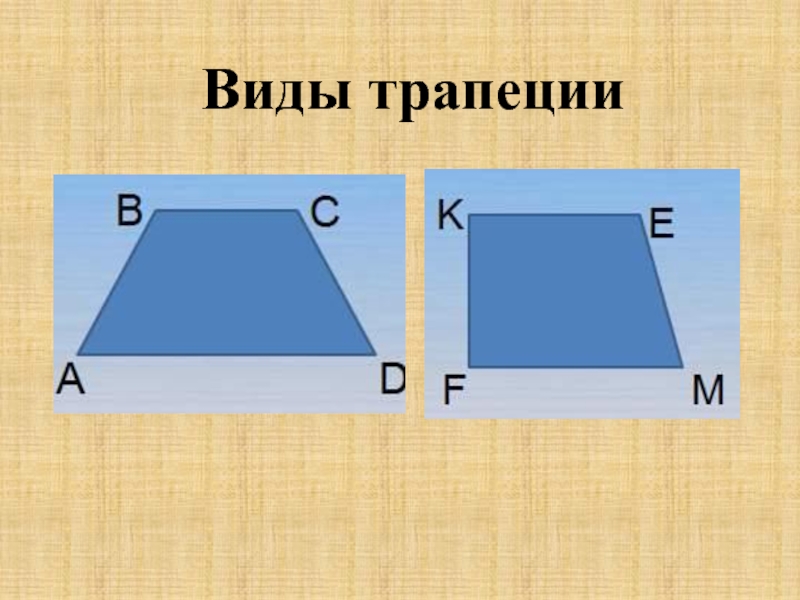

7. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.

8. Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.

Свойства и признаки равнобедренной трапеции

1. В равнобедренной трапеции углы при любом основании равны.

2. В равнобедренной трапеции длины диагоналей равны.

3. Если трапецию можно вписать в окружность, то трапеция – равнобедренная.

4. Около равнобедренной трапеции можно описать окружность.

5. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.

Вписанная окружность

Если в трапецию вписана окружность с радиусом и она делит боковую сторону точкой касания на два отрезка — и , то

Площадь

или где – средняя линия

Смотрите хорошую подборку задач с трапецией (входят в ГИА и часть В ЕГЭ) здесь и здесь.

Смотрите также площадь трапеции.

Форма: трапеция — элементарная математика

Значение

Трапеция — четырехугольник, по крайней мере, с одной парой параллельных сторон. Никакие другие особенности не имеют значения. (В англоязычных странах за пределами Северной Америки эквивалентным термином является трапеция.)

Параллельные стороны могут быть вертикальными, горизонтальными или наклонными. Фактически, по определению, даже это трапеция, потому что у нее есть «по крайней мере одна пара параллельных сторон» (и никакие другие особенности не имеют значения) как есть.На этих фигурах две другие стороны также параллельны, и поэтому они удовлетворяют не только требованиям для того, чтобы быть трапецией (четырехугольник, по крайней мере, с одной парой параллельных сторон), но также и требованиям для того, чтобы быть параллелограммом.

Приведенное выше определение принято в математическом сообществе и, все чаще, в образовательном сообществе.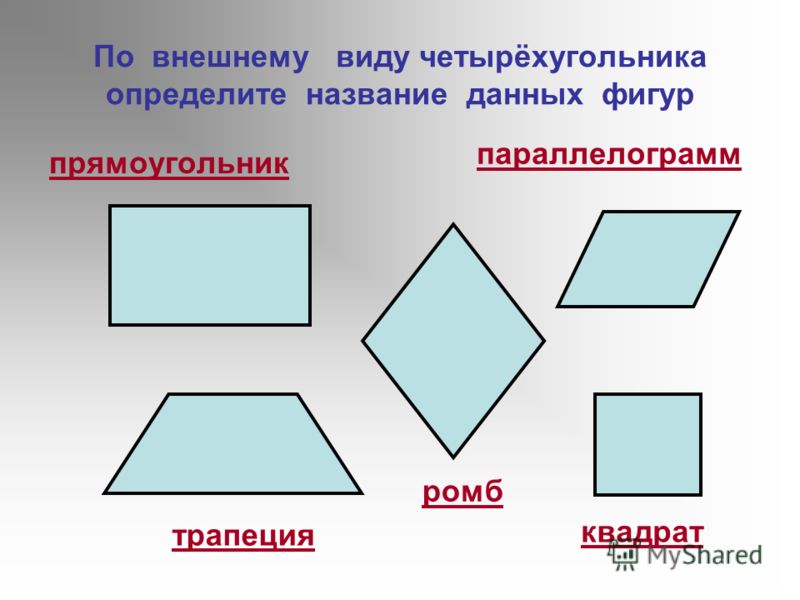 Многие источники, связанные с K-12 образованием, исторически ограничивали определение трапеции, требуя ровно одной пары параллельных сторон.Этот более узкий вид исключает параллелограммы как подмножество трапеций и оставляет только такие фигуры, как, и. Это более узкое определение трактует трапеции как треугольники с «одной вершиной, отрезанной параллельно противоположной стороне». Даже с ограниченным определением ученикам важно видеть нестандартные примеры — асимметричные, как примеры зеленого и коричневого, и в неуровневой ориентации, как красный пример, — чтобы создаваемое ими изображение фокусировалось на основных особенность: пара параллельных сторон.

Классифицирующие трапеции

Параллелограммам с особыми характеристиками, такими как прямые углы или все совпадающие стороны (или и то и другое), даны собственные отличительные имена: прямоугольник, ромб и квадрат. Единственная особенность трапеции , которой присвоено собственное отличительное имя, — это вторая пара параллельных сторон, которая превращает особую трапецию в параллелограмм.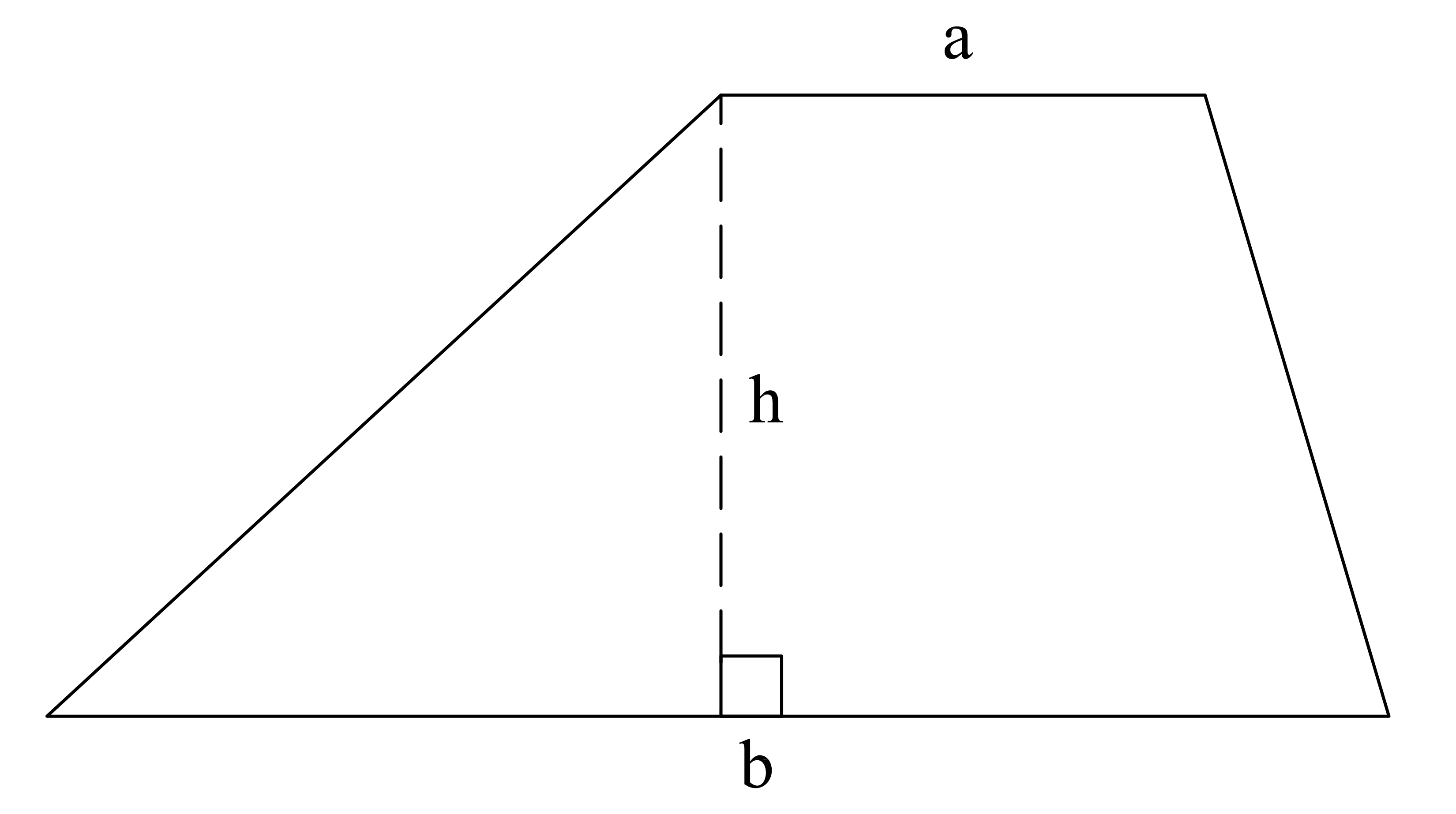 Когда две стороны (кроме оснований) имеют одинаковую длину, трапеция называется равнобедренной («равнобедренная трапеция»), так же как треугольники с двумя сторонами равной длины (кроме основания) называются равнобедренными треугольниками.Никакие другие отличительные названия не используются для трапеций с особыми характеристиками (например, прямые углы или три совпадающие стороны).

Что одним словом?

Суффикс -оид предполагает, что он «похож» на что-то, но не совсем то же самое: сфероид похож на сферу, но не обязательно на идеальную сферу; гуманоид похож на человека, но не на человека; и трапеция имеет форму трапеции, но не трапеция. Современное значение trapeze предполагает цирковые качели ( — это , часто трапециевидная форма, сиденье параллельно перекладине, на котором висит трапеция), но trapeze первоначально означало «стол», от tra ( «четверка», как в tetra- ) pez («нога» или «ступня», которые мы чаще видим как ped , как в pedal или pedestrian ).

Трапеция

(Перейти к области трапеции или периметру трапеции)

Трапеция — это четырехсторонняя плоская форма с прямыми сторонами, имеющая пару противоположных сторон, параллельных (отмечена стрелками ниже):


Трапеция		Равнобедренная трапеция

Трапеция:

	имеет пару параллельных сторон
	— это равнобедренная трапеция , , когда она имеет равных углов от параллельной стороны
	называется « трапеция » в Великобритании (см. Ниже)

Люфт трапецией:

изображения / geom-quad. js? mode = трапеция

Параллельные стороны — это «основания»

Две другие стороны — «ножки»

Расстояние (под прямым углом) от одной базы до другой называется «высотой»

Площадь трапеции

Площадь — это среднее значение длины двух баз, в раз превышающее высоту :

Площадь = a + b 2 × h

Пример: два основания трапеции составляют 6 м и 4 м, а высота — 3 м.Какова его площадь?

Площадь = 6 м + 4 м 2 × 3 м = 5 м × 3 м = 15 м ²

Инструмент «Площадь многоугольника путем рисования» полезен, когда вы можете нарисовать трапецию.

Периметр трапеции

Периметр — это расстояние по краям.

Периметр равен сумме длин всех сторон :

Периметр = a + b + c + d

Пример: Трапеция имеет длину стороны 5 см, 12 см, 4 см и 15 см.

Каков ее периметр?

Периметр = 5 см + 12 см + 4 см + 15 см = 36 см

Медиана трапеции

Медиана (также называемая средней линией или срединным сегментом) — это линейный сегмент на полпути между двумя основаниями.

Средняя длина — это среднее значение двух базовых длин:

м = а + б 2

Вы можете вычислить площадь, зная медианное значение, это просто медиана, умноженная на высоту:

Площадь = mh

Трапеция

Трапеция (UK: trapezoid) — четырехугольник без параллельных сторон.

Определения США и Великобритании поменялись местами, например:

	Трапеция	Трапеция
США:	Пара параллельных сторон	НЕТ параллельных сторон
Великобритания:	НЕТ параллельных сторон	Пара параллельных сторон

9131, 9132, 9133, 9134, 9135, 9136, 9137, 9138, 9139, 9140

Что такое трапеция? [Определение, факты и пример]

Что такое трапеция?

Трапеция, также известная как трапеция, представляет собой плоскую замкнутую форму, имеющую 4 прямые стороны с одной парой параллельных сторон.

Параллельные стороны трапеции называются основаниями, а непараллельные стороны — ножками. У трапеции тоже могут быть параллельные ножки. Параллельные стороны могут быть горизонтальными, вертикальными или наклонными.

Расстояние по перпендикуляру между параллельными сторонами называется высотой.

Примеры :

Без примеров :

Типы трапеций

Трапеция бывает трех типов, а именно

1. Правая трапеция : Имеет пару прямых углов.

2. Равнобедренная трапеция : имеет одинаковую длину непараллельных сторон. На изображении стороны AD и BC равны.

3. Чешуйчатая трапеция : у нее нет равных углов и равных сторон.

Свойства трапеции

Трапеция называется параллелограммом, если обе пары ее противоположных сторон параллельны.
Трапеция — это квадрат, если обе пары его противоположных сторон параллельны; все его стороны равной длины и расположены под прямым углом друг к другу.
Трапеция может быть прямоугольником, если обе пары ее противоположных сторон параллельны; его противоположные стороны равны по длине и расположены под прямым углом друг к другу.

Примеры из реальной жизни

Некоторые из многих примеров трапеции — это лицевая сторона коробки для попкорна, сумочки и мостов.

Интересные факты

Трапеция была известна как τραπέζιον «ловушка» на древнегреческом, что буквально означает «столик», а также означает «неправильный четырехугольник». Кроме того, «оид» в переводе с древнегреческого означает «похожий».
Слово трапеция было введено в английский язык в 1570 году. Марин Прокл был первым, кто использовал слово «трапеция» в первой книге «Начала» Евклида.

Что такое трапеция? (Определение, свойства и видео) // Tutors.com

Содержание

Что такое трапеция?
Определения трапеций
Уголки трапеции
Свойства трапеции
Трапеции
Виды трапеций

Что такое трапеция?

Трапеция — четырехугольник с одной парой параллельных сторон.Трапеция — это:

Плоская фигура (плоская)
Замкнутая фигура (имеет внутреннюю и внешнюю)
Многоугольник (прямые стороны)
Четырехугольник (четыре прямые стороны)

Чтобы сделать трапецию, вам понадобится треугольник. Подойдет любой треугольник: прямой, тупой, равнобедренный, разносторонний. Отрежьте верхнюю часть треугольника так, чтобы разрез был параллелен нижней части треугольника. Теперь у вас есть более крошечный треугольник и трапеция.

Поскольку для определения требуется только одна пара параллельных сторон, две другие стороны можно расположить разными способами, создавая четыре внутренних угла, которые в сумме всегда составляют 360 °.

Определения трапеций

Мы уже знаем, что трапеция похожа на нижнюю часть треугольника, если от нее отрезать меньший треугольник. Вы также можете сделать трапецию из четырех отрезков или четырех прямых объектов.

Используйте все, что вам нравится: сырые спагетти, карандаши, палочки от леденцов; все, что у вас есть под рукой. Четыре прямых (линейных) объекта могут быть четырех разных длин или трех разных длин (два из них могут быть одинаковыми).

Положите два объекта вниз или нарисуйте два отрезка линии, чтобы они были параллельны (равноудалены).Сделайте их горизонтально по отношению к вам. Поместите два других объекта слева и справа от этих двух или нарисуйте их так, чтобы все восемь конечных точек соприкасались.

Вот и все, трапеция! Горизонтальные части — это основания . Последние две части, которые вы нарисовали или положили (на левом и правом концах), называются ножками трапеции.

Уголки трапеции

Обратите внимание, что мы не беспокоились ни о каком из внутренних углов, поскольку сохранение двух сторон параллельными заставляет остальную часть трапеции встать на место. Углы сортируются и складываются в 360 °.

Высота трапеции — это ее высота. Пусть вас не обманывают покатые ножки — если они наклонены, то длиннее высоты. Высота всегда измеряется от основания (любой параллельной стороны) до другой стороны под прямым углом к основанию.

Вы можете провести перпендикулярную линию в любом месте основания трапеции, и когда она касается противоположной, параллельной стороны, ее длина равна высоте.

Свойства трапеции

Трапеция — это параллелограмм?

Вы можете определить любую трапецию, если это четырехугольник с одной парой параллельных сторон.Многие математики включают параллелограммы как типы трапеций, потому что, конечно, параллелограмм имеет по крайней мере одной пары параллельных сторон. Другие математики исключают параллелограммы, говоря, что у трапеции должно быть ровно одной пары параллельных сторон.

Еще одним отличительным свойством всех трапеций является то, что любые два смежных внутренних угла будут дополнительными (добавить к 180 °).

Трапеции

Обычно для максимальной ясности на изображениях и рисунках трапеций показаны две параллельные стороны, идущие горизонтально, причем более длинная сторона обращена вниз в качестве основания.Однако будьте готовы увидеть трапеции в любой ориентации . Трапецию можно нарисовать или изобразить либо с ногой внизу, либо с более короткой параллельной стороной внизу.

Поскольку параллельные стороны — единственные, которые могут быть основаниями, даже когда трапеция рисуется с ногой внизу и горизонтально, это , а не основание. Это все еще нога.

Основание обычно представляет собой более длинную параллельную сторону, но если трапеция рисуется с более короткой параллельной стороной внизу, то это основание.

Типы трапеций

Поскольку трапеции могут возникать в виде треугольников, они имеют общие названия, полученные от типов треугольников:

Scalene trapezoid — Начинается как разносторонний треугольник
Равнобедренная трапеция — начиналась как равнобедренный треугольник
Правая трапеция — Когда-то был прямоугольный треугольник
Тупая трапеция — Как тупой треугольник
Острая трапеция — как острый треугольник

Трапеция из чешуи

Разносторонняя трапеция имеет четыре стороны неравной длины. Основания параллельны, но разной длины. Две ножки разной длины.

Равнобедренная трапеция

Равнобедренная трапеция имеет ножки одинаковой длины. Основания параллельны, но разной длины.

Трапеция правая

Прямоугольная трапеция имеет один прямой угол (90 °) между основанием и ножкой.

Тупая трапеция

Тупая трапеция имеет один внутренний угол (образованный основанием или опорой ) больше 90 °.

Острая трапеция

Острая трапеция имеет оба внутренних угла (образованные более длинным основанием и ножками ) размером менее 90 °.

Краткое содержание урока

Используя всего четыре линии и четыре внутренних угла, мы построили трапецию , узнали, что делает трапецию уникальной (пара параллельных сторон), каковы различные части трапеции и названия пяти специальных трапеций.

Следующий урок:

Как найти площадь трапеции

Площадь трапеции — пояснения и примеры

Напомним, трапеция , также называемая трапецией , , представляет собой четырехугольник с одной парой параллельных сторон и другой парой непараллельных сторон. Подобно квадрату и прямоугольнику, трапеция также плоская. Следовательно, это 2D.

В трапеции параллельные стороны называются основаниями, а пара непараллельных сторон — ногами.Расстояние по перпендикуляру между двумя параллельными сторонами трапеции называется высотой трапеции.

Проще говоря, основание и высота трапеции перпендикулярны друг другу.

Трапеции могут быть как правыми трапециями (два угла 90 градусов), так и равнобедренными трапециями (две стороны одинаковой длины). Но иметь один прямой угол невозможно, потому что у него есть пара параллельных сторон, которые ограничивают его, образуя два прямых угла одновременно.

Из этой статьи вы узнаете:

Как найти площадь трапеции,
Как получить формулу площади трапеции и,
Как найти площадь трапеции с помощью трапеции формула площади.

Как найти площадь трапеции?

Площадь трапеции — это область, покрытая трапецией в двухмерной плоскости. Это пространство, заключенное в 2D-геометрии.

На рисунке выше трапеция состоит из двух треугольников и одного прямоугольника.Следовательно, мы можем вычислить площадь трапеции, взяв сумму площадей двух треугольников и одного прямоугольника.

Вывести формулу площади трапеции

Площадь трапеции ADEF = (½ x AB x FB ) + ( BC x FB ) + (½ x CD x EC )

= ( ¹ / ₂ × AB × h ) + ( BC × h ) + (¹ / ₂ × CD × h )

= ¹ / ₂ × h × ( AB + 2 BC + CD )

= ¹ / ₂ × h × ( FE + AD )

Но, FE = b ₁ и AB = b ₂

Следовательно, Площадь a трапеция ADEF ,

= ¹ / ₂ × h × (b ₁ + b ₂) ……………….(Это формула площади трапеции)

Формула площади трапеции

Согласно формуле площади трапеции, площадь трапеции равна половине произведения высоты и суммы двух оснований.

Площадь = ½ x (сумма параллельных сторон) x (расстояние по перпендикуляру между параллельными сторонами).

Площадь = ½ h (b ₁ + b ₂)

Где h — высота, а b _1, и b ₂ — параллельные стороны трапеции.

Как определить площадь неправильной трапеции?

Неправильная трапеция имеет непараллельные стороны неравной длины. Чтобы найти его площадь, нужно найти сумму оснований и умножить ее на половину высоты.

В вопросе иногда не хватает высоты, что можно найти с помощью теоремы Пифагора.

Как найти периметр трапеции?

Вы знаете, что периметр — это сумма всех длин внешнего края фигуры.Следовательно, периметр трапеции — это сумма длин всех 4 сторон.

Пример 1

Вычислите площадь трапеции, высота которой составляет 5 см, а основания — 14 см и 10 см.

Решение

Пусть b ₁ = 14 см и b ₂ = 10 см

Площадь трапеции = ½ h (b ₁ + b ₂) см ²

= ½ x 5 (14 + 10) см ²

= ½ x 5 x 24 см ²

= 60 см ²

Пример 2

Найдите площадь трапеции с высота 30 мм, а основания 60 мм и 40 мм.

Раствор

Площадь трапеции = ½ h (b ₁ + b ₂) кв. Единиц

= ½ x 30 x (60 + 40) мм ²

= ½ x 30 x 100 мм ²

= 1500 мм ²

Пример 3

Площадь трапеции составляет 322 квадратных дюйма. Если длины двух параллельных сторон трапеции составляют 19 дюймов и 27 дюймов, найдите высоту трапеции.

Раствор

Площадь трапеции = ½ часа (b ₁ + b ₂) кв.единицы.

⇒ 322 квадратных дюйма = ½ x в x (19 + 27) кв. дюймов

⇒ 322 квадратных дюйма = ½ x h x 46 кв. дюймы

⇒ 322 = 23h

Разделите обе стороны на 23.

h = 14

Итак, высота трапеции составляет 14 дюймов.

Пример 4

Учитывая, что высота трапеции составляет 16 м, а длина одного основания — 25 м. Рассчитайте размер другого основания трапеции, если его площадь составляет 352 м ².

Решение

Пусть b ₁ = 25 м

Площадь трапеции = ½ h (b ₁ + b ₂) кв. Единиц

⇒ 352 м ² = ½ x 16 м x (25 m + b ₂) кв. Единиц

⇒ 352 = 8 x (25 + b ₂)

⇒ 352 = 200 + 8b ₂

Вычтите 200 с обеих сторон.

⇒ 152 = 8b ₂

Разделите обе части на 8, чтобы получить;

b ₂ = 19

Следовательно, длина другого основания трапеции составляет 19 м.

Пример 5

Рассчитайте площадь трапеции, показанной ниже.

Решение

Поскольку стороны (непараллельные стороны) трапеции равны, высоту трапеции можно рассчитать следующим образом;

Чтобы получить основание двух треугольников, вычтите 15 см из 27 см и разделите на 2.

⇒ (27-15) / 2 см

⇒ 12/2 см = 6 см

12 ² = h ² + 6 ² По теореме Пифагора высота (h) рассчитывается как;

144 = h ² + 36.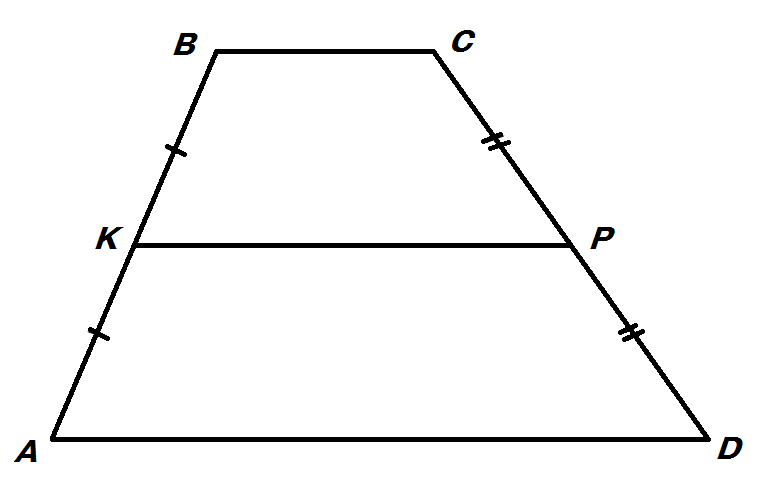

Вычтем 36 с обеих сторон.

h ² = 108.

h = 10,39 см.

Следовательно, высота трапеции 10,39 см.

Теперь вычислите площадь трапеции.

Площадь трапеции = ½ ч (b ₁ + b ₂) кв. единицы.

= ½ x 10,39 x (27 + 15) см ².

= ½ x 10,39 x 42 см ².

= 218,19 см ².

Пример 6

Одно основание трапеции на 10 м больше высоты.Если другое основание составляет 18 м, а площадь трапеции равна 480 м ², найдите высоту и основание трапеции.

Решение

Пусть высота = x

Другая база равна 10 м, чем высота = x + 10.

Площадь трапеции = ½ h (b ₁ + b ₂) Кв. единицы.

Путем подстановки

480 = ½ * x * (x + 10 + 18)

480 = ½ * x * (x + 28)

Удалите скобки с помощью свойства распределения.

480 = ½x ² + 14x

Умножьте каждый член на 2.

960 = x ² + 28x

x ² + 28x — 960 = 0

Решите квадратное уравнение, чтобы получить;

x = — 48 или x = 20

Подставьте положительное значение x в уравнение высоты и основания.

Высота: x = 20 м.

Другая база = x + 10 = 10 + 20 = 30 м.

Следовательно, другое основание и высота трапеции равны 30 и 20 м соответственно.

Практические задачи
Найдите площадь трапеции, у которой есть параллельные основания длиной 9 единиц и 12 единиц, а высота равна 15 единицам.
Для трапециевидной фигуры сумма параллельных оснований составляет 25 м, а высота — 10 м. Определите площадь этой фигуры.
Рассмотрим трапецию площадью 112b квадратных футов, где b — более короткая базовая длина. Какова высота этой трапеции, если длины двух параллельных оснований таковы, что одно основание в два раза больше другого основания?

Предыдущий урок | Главная страница | Следующий урок
Бесплатная распечатка трапециевидной формы — Халява в поисках мамы
Это ловушка! Эээ, вообще-то это трапеция! 🙂 Бесплатная печатная форма трапеции, чтобы быть еще более конкретной, а также углубленное освежение, которое охватывает все, от основ (что такое трапеция) до продвинутого (как найти площадь трапеции).
Ваш ребенок когда-нибудь просил вас помочь с его или ее домашним заданием, и вы сразу знали ответ, не спрашивая Google, Siri, Alexa или любого другого электронного всезнайки? Это здорово, не правда ли? Я имею в виду, серьезно, конфетти и воздушные шары должны сыпаться с потолка!
К сожалению, этого, вероятно, не произойдет, когда дело доходит до сложных геометрических форм, таких как трапеции.
Это потому, что (и будьте честны), когда в последний раз вас спрашивали, какова площадь трапеции или формула трапеции для определения периметра? Я знаю когда! Когда вы брали геометрию! Да, давайте посмотрим правде в глаза, большинство из нас не использует эти вещи во взрослой жизни, но не волнуйтесь, это будет нашим маленьким секретом.
Я создал шаблон трапеции для печати (прокрутите вниз), который может рассказать вам, как выглядит трапеция, а также помочь продемонстрировать некоторые математические концепции, такие как площадь трапеции, поэтому обязательно загрузите его! Как упоминалось выше, в дополнение к бесплатной печатной форме трапеции, этот пост включает в себя напоминание о трапеции. Обновление будет охватывать:
Что такое трапеция, включая свойства трапеции, например, сколько сторон у трапеции.
Как трапеции по сравнению с другими формами? Например, прямоугольник — это трапеция? Трапеция — это параллелограмм?
Базовая геометрия трапеции, включая формулу площади трапеции, как найти периметр трапеции и как найти объем форм трапеции.
Многое другое!
Бонус: И это еще не все! Отправляйтесь в магазин Freebie Finding Mom, чтобы получить мой 132-страничный набор фигур прямо сейчас!
В этом наборе из 132-страничных рабочих листов форм для печати в магазине Freebie Finding Mom вы получите рабочих листов для трассировки фигур , рабочие листы сопоставления форм, раскраски фигур, листы подсчета фигур, рабочие листы шаблонов фигур, формы для печати , 2D-диаграммы фигур и карточки с фигурами.Если вам нужны листы фигур для дошкольников или листы фигур для детского сада, вы найдете это и многое другое здесь! Получите этот набор невероятных форм прямо сейчас!
Psst! Большая часть информации о форме трапеции предназначена для детей школьного возраста (а не для вашего дошкольника). Однако, если у вас дома есть маленький, вы все равно можете использовать этот шаблон трапеции для печати! Возможно, его можно было бы использовать как:
Часть проекта декоративно-прикладного искусства; например, чтобы научить вашего ребенка рисовать трапецию в рамках цирковой сцены (например, на предмете, на котором стоит слон или инспектор манежа).
Простая раскраска. Раскрашивание помогает улучшить координацию движений, способствует творчеству и расслаблению. (Psst! Больше раскрасок, в том числе забавных вариантов для взрослых, можно найти здесь бесплатных распечатанных раскрасок.)
Фрагмент самодельной игры на поиск совпадений. В вашей игре на совпадение можно использовать фигуры, буквы, числа и т. Д., Чтобы помочь вашему ребенку развить фокус и зрительную память! Например, вы можете предложить ему или ей сопоставить прописные буквы со строчными буквами.(Psst! Вы можете бесплатно скачать пузырьковых букв для печати и пузырьковых чисел здесь .)
Чувствуете себя супер вдохновленным? Потрясающе … давай продолжим хорошие времена (или нет, потому что трапеции не круглые, ха-ха)! Во-первых, определение трапеции.
Определение трапеции
Прежде чем мы сможем ответить на такие вопросы, как трапеция четырехугольником, как определить площадь трапеции и какова формула объема трапеции, давайте начнем с основ.Вроде очень простой. Что такое трапеция?
Базовое определение трапеции — это замкнутая форма с четырьмя прямыми сторонами, у которой есть одна пара противоположных сторон, которые параллельны. Вот некоторые свойства трапеции, которые могут прояснить ее:
Замкнутая форма.
Сколько сторон у трапеции? Их всегда четыре.
Одна пара противоположных сторон параллельна друг другу.
Может иметь прямые углы, что называется прямой трапецией.
Может иметь конгруэнтные (равные) стороны, что называется равнобедренной трапецией.
Звучит просто, правда? Что ж, у трапеций есть один спорный аспект. В некоторых местах трапеция определяется как имеющая только один набор параллельных сторон. (Это называется исключительным определением.)
В других местах трапеция определяется как имеющая по крайней мере один набор параллельных сторон, но может иметь и два набора. (Это называется всеобъемлющим определением.) Придерживайтесь того определения, которое ваш учитель говорит вам использовать! И кто знал, что ответ на вопрос, что форма трапеции может быть спорным?
Что такое правая трапеция?
Когда кто-то спрашивает о правильной трапеции, это не значит, что это неправильная трапеция.(Ха-ха, понятно?) Правая трапеция просто означает, что форма трапеции имеет прямые (90 градусов) углы.
Каковы свойства равнобедренной трапеции?
Свойства равнобедренной трапеции такие же, как и у других свойств трапеции, за исключением того, что они должны иметь две конгруэнтные (равной длины) стороны.
Все еще не можете вызвать изображение трапеции? Просто прокрутите вниз до печатной формы, чтобы увидеть, как выглядит трапеция! Распечатываемая форма трапеции покажет вам, сколько сторон у трапеции, и будет полезна, когда мы пройдемся по большей части освежения.
Что такое форма трапеции по сравнению с. Другие формы
Исходя из свойств трапеции и определения, приведенного выше, мы технически знаем ответ на вопрос «что такое трапеция?» однако как это соотносится с другими формами?
Трапеция — параллелограмм?
Ну, во-первых, что такое параллелограмм? Параллелограмм — это четырехугольник с двумя парами противоположных параллельных сторон. Противоположные стороны также равны по длине.
Итак, трапеция — это параллелограмм? Что ж, может быть, если вы используете всеобъемлющее определение, но это не обязательно.Вернитесь к свойствам, определяющим трапецию — только одна пара противоположных сторон должна быть параллельна друг другу.
Примечание. Помните, что некоторые классы учат, что трапеция может иметь только одну пару параллелей. Если именно так ваш учитель хочет определять формы трапеции, ваша трапеция никогда не может быть параллелограммом!
Трапеция — четырехугольник?
Хорошо, вы уже знаете ответ на вопрос «трапеция — четырехугольник», потому что мы так сказали в разделе определения трапеции.(Это четырехугольник.) Однако для ясности давайте определим, что такое четырехугольник: четырехугольник — это двумерная замкнутая форма, имеющая четыре прямые стороны.
Популярная викторина: Всегда ли трапеция является четырехугольником? Музыка Cue the Jeopardy. Ответ: трапеция, всегда четырехугольник — да. Это потому, что трапеция всегда замкнута и всегда имеет четыре прямые стороны.
Прямоугольник — это трапеция?
Ответ — прямоугольник, трапеция будет зависеть от того, какое определение, исключительное или включающее, вы используете.Сначала давайте посмотрим на определение прямоугольника. Прямоугольник — это замкнутая фигура с четырьмя прямыми сторонами и четырьмя прямыми углами, у которых противоположные (параллельные) стороны равны по длине.
Итак, является ли прямоугольник трапецией? Опять же, это может быть, если вы используете всеобъемлющее определение, потому что трапеция может иметь два набора параллельных сторон и может иметь прямые (90 градусов) углы.
Квадрат — это трапеция?
Начнем с определения квадрата.Квадрат — это четырехугольник с четырьмя равными сторонами, четырьмя равными углами в 90 градусов и противоположными сторонами, которые параллельны. Итак, квадрат — это трапеция?
Не звучит как зажившая пластинка, но опять же, ответ на вопрос — квадрат трапеции, будет зависеть от того, используете ли вы исчерпывающее определение. Если вы используете исчерпывающее определение, ответ таков: трапеция может быть квадратом. если вы используете исключительное определение, ответ будет отрицательным, потому что квадрат имеет два набора параллельных сторон.
Является ли трапеция многоугольником?
Многоугольник — это двумерная замкнутая форма, имеющая как минимум три стороны и три угла. Это означает, что ответ — трапеция, а многоугольник — да!
(Ответ — трапеция, а многоугольник — да, независимо от того, какое определение, исключительное или включающее, вы используете!)
Уф! Трапеция может означать много разных вещей, не так ли? Если у вас возникли проблемы с изображением этой волшебной формы, меняющей форму, прокрутите вниз и найдите пример трапеции!
Скачать форму трапеции для печати
Кто знал, что трапеции могут быть столь же противоречивыми, как и поп-звезды, верно? 😉 На самом деле, я готов поспорить, что в некоторых кругах дискуссии по поводу инклюзивного vs.эксклюзивное определение разгорается так же жарко, как политические дебаты! К счастью, мы переходим к математической части статьи.
Но сначала обязательно возьмите распечатанный шаблон трапеции ниже. Он не только демонстрирует, как выглядит трапеция с изображением трапеции, но также может быть отличным примером трапеции для некоторых математических концепций, которые мы собираемся рассмотреть.
Бонус: Вы думали, что на этом изображении трапеции отсутствует цвет? Нет проблем, позвольте мне украсить ваш день (буквально) с помощью этого предварительно окрашенного бесплатного трапециевидного шаблона для печати .
Сколько линий симметрии у трапеции
Прежде чем мы перейдем к тому, сколько линий симметрии у трапеции, давайте определим, что такое «линия симметрии».
Итак, ответ на вопрос, сколько линий симметрии у трапеции, зависит от того, как она выглядит… и да, от того, какое определение вы используете.
Например, если вы используете инклюзивное определение, трапеция может быть квадратом, а квадраты имеют 4 линии симметрии. Если вы используете исключительное определение, трапеция будет иметь либо 1 линию симметрии (для равнобедренной трапеции), либо 0 линий симметрии.
Линия симметрии — это линия, которая идеально разрезает фигуру пополам. Это означает, что если бы вы сложили фигуру по этой линии, обе половины точно совпали бы.
Для детей младшего возраста эти распечатываемых рабочих листов трапеции могут быть более быстрыми.
Как найти периметр трапеции
Если вы немного нервничаете по поводу математической части этого поста, сделайте глубокий вдох. Мы собираемся начать с чего-то простого — формулы трапеции для определения периметра.Подождите, не паникуйте! Я знаю, что когда начинают употреблять такие слова, как «формула», это может быть довольно пугающим, но эта «формула» настолько проста.
Когда мы говорим о периметре чего-либо, все, о чем мы говорим, — это измерение внешней части формы. Это означает, что для того, чтобы найти периметр трапеции, все, что вам нужно сделать, это сложить измерения всех четырех сторон. Ага, вот и все, базовое дополнение!
Формула трапеции для определения периметра будет выглядеть примерно так:
Периметр = a + b + c + d
В этой формуле a, b, c и d представляют четыре стороны трапеции.
Обычно вам дается изображение трапеции, на котором написаны все размеры сторон. Тогда вы просто сложите их. Для более сложной задачи вам могут дать равнобедренную трапецию, размер которой измеряется только с трех сторон, но это нормально! Почему? Потому что мы знаем, что у равнобедренной трапеции две стороны равны по длине.
Совет: эта формула будет работать для определения периметра любой четырехсторонней формы; однако помните, что если вы имеете дело с квадратом, все четыре стороны равны, а у прямоугольника две противоположные стороны равны по длине.
Как найти площадь трапеции
Какова площадь трапеции? Что ж, когда мы говорим о площади, мы говорим об общем пространстве, которое занимает объект (например, трапеция). Итак, периметр — это внешнее измерение, а площадь — это полное внутреннее пространство, которое занимает. Если вы смотрите на распечатываемое цветное трапециевидное изображение, окрашенная часть является областью.
Хотя область уравнения трапеции может показаться пугающей, если вы не имеете дело с очень большими числами или, возможно, десятичными числами, вы, скорее всего, сможете решить его вручную.Правильно, калькулятор не нужен! Я верю в тебя! 😉
Совет. Область уравнения трапеции, которым я собираюсь поделиться с вами в этом разделе о том, как найти площадь трапеции, предназначена для трапеций с эксклюзивным определением. Нет, я не принимаю здесь чью-либо сторону. Есть и другие (возможно, более простые) формулы, которые вы можете использовать для определения площади квадрата или прямоугольника. Опять же, этот раздел специально посвящен тому, как найти площадь трапеции!
Для формулы площади трапеции вам необходимо знать размер двух оснований (то есть верхней и нижней линий трапеции) и высоту трапеции, также известную как «высота».«После того, как вы посмотрите на свое изображение трапеции и сделаете эти измерения, вы готовы применить формулу площади трапеции!
Какова формула площади трапеции?
Площадь = ((a + b) / 2) * h
Не паникуйте! Давайте разберемся с этой частью уравнения трапеции. В формуле «a» и «b» — это размер ваших двух оснований, а «h» — это высота (или высота) трапеции.
Чтобы рассчитать площадь трапеции, вам необходимо запомнить порядок действий.При решении математических задач вы хотите выполнять действия в следующем порядке:
Круглые скобки
Показатели
Умножение или деление
Сложение или вычитание
Это означает, что для определения площади трапеции вы собираетесь выполнять действия в следующем порядке:
Сложите «a» и «b» (размер ваших двух оснований). Это потому, что они указаны в скобках.
Разделите сумму «a» + «b» на 2.
Умножьте полученное число на «h»
Угадайте, что? Теперь вы не только знаете, какова формула площади трапеции, но и знаете, как рассчитать площадь трапеции!
Какой объем трапеции
Технически ответ на вопрос, какой объем трапеции или какова формула для объема трапеции, «неприменим.(Хотя вам, вероятно, не следует писать это в домашней работе вашего ребенка!) Это потому, что трапеции — это двухмерные фигуры, а понятие объема применимо к трехмерным объектам.
Посмотрите на свое изображение в форме трапеции. Плоская, правда? Он ничего не мог вместить … следовательно, у него нет громкости.
Однако вы могли бы ответить на вопрос «какова формула объема трапециевидной призмы». Формула требует от вас найти площадь основания, что в точности совпадает с нахождением площади трапеции (см. Предыдущий раздел), а затем умножением этого числа на длину призмы.
Итак, помните, если кто-то спросит вас «какова формула для определения объема трапеции», им действительно понадобится формула для определения объема трапециевидной призмы!
Бесплатная печать 2D-фигур
Готовы поговорить о менее спорных формах? Если да, то вот еще больше печатаемых 2D-фигур, которые вы можете скачать прямо сейчас!
Загрузите эту бесплатную распечатываемую диаграмму 2D-фигур в черно-белом или эту бесплатную печатную диаграмму 2D-фигур в цвете .
Или, если вам понравилась конкретная форма, вы можете скачать ее здесь:
Раскраски за пределами печатной формы трапеции
Все ли споры о трапеции заставили вас завязать узлы? Расслабьтесь с раскраской! Раскрашивание может вызвать состояние расслабления, подобное медитации. Вот несколько бесплатных загрузок:
чтобы сделать свою домашнюю игру на соответствие:
Еще больше шаблонов
Оставайтесь изобретательными и креативными с еще большим количеством бесплатных шаблонов для печати!
Как нарисовать трапецию
Хотите знать, как нарисовать трапецию? Попробуйте один из этих двух вариантов:
Выломайте линейку и аккуратно нарисуйте трапецию, измерив ваши линии, чтобы убедиться, что они прямые и что хотя бы один набор (о-о, больше споров!) Параллелен.
Возьмите трапециевидную форму для печати из этого поста и обведите ее! (Посмотрите видео в этом посте для примера; в то время как видео фокусируется на том, как рисовать пузырьковые буквы, концепция такая же, как и для рисования трапеции.)
Основания трапеции, ножки, углы и площадь, правила и формулы
Трапеция — это четырехугольник с одной парой параллельных прямых
Основания — две параллельные линии называются основаниями.
Ноги — две непараллельные линии — это ноги.
Недвижимость
Свойство №1) Углы на одной стороне опоры называются смежными углами и являются дополнительными (еще )
Свойство № 2) Площадь трапеции = $$ Площадь = высота \ cdot \ left (\ frac {\ text {sum base}} {2} \ right) $$ (еще )
Объект № 3) Трапеции имеют средний сегмент, соединяющий вершины ног (еще )
Смежные углы трапеции
Углы на одной стороне ножки называются смежными углами, например $$ \ angle A $$ и $$ \ angle D $$ являются дополнительными.По той же причине $$ \ angle B $$ и $$ \ angle C $$ являются дополнительными.
Задача 1
$$ \ angle ZWX = 180 — 44 = 136 ° $$
Задача 2
Используйте теорему о смежных углах для вычисления m $$ \ angle MLO $$.
Показать ответ
$$ \ angle MLO = 180-124 = 56 ° $$
Задача 3
Найдите значение x на трапеции ниже, затем определите меру углов $$ \ angle WXY $$ и $$ \ angle XYZ $$.
Показать ответ
Задача 4
Что не так с трапецией LMNO, изображенной ниже? (Объясните, почему LMNO не может быть трапецией, основываясь на предоставленной информации) .
Показать ответ
Если LMNO представляет собой трапецию и ее основания LO и MN параллельны, то $$ \ angle MNO $$ и $$ \ angle NOL $$, которые должны быть дополнительными, сумма этих углов не равна 180 111 + 68 ≠ 180. 2 $
Средний отрезок трапеции:
Задача 6
Используйте теорему о среднем сегменте, чтобы определить длину включения среднего сегмента.
Длина мидсегмента
Чтобы вычислить длину среднего сегмента, найдите среднее значение длины оснований среднего сегмента = (6 + 4) / 2 = 5.
Быстрый обзор Midpoint
Самая важная вещь, о которой следует помнить, — это то, что средняя точка делит линию пополам (разрезает линию на две равные половины).
Показать среднюю точку
Средняя точка красного сегмента, изображенного ниже, — это точка $$ (A, 2b) $$ (нажмите кнопку ниже, чтобы увидеть).
Средний сегмент трапеции — это сегмент, соединяющий середины непараллельных сторон трапеции.
На трапеции ниже середины непараллельных сторон — это точки S и V. Средний сегмент — это красный отрезок линии от S до V.
Пример среднего сегмента
Трапеция # 10 Шаг 1 Расчет длины оснований. Верхняя база:
$$ 35–16 = 9 $$
Шаг 2
Расчет низкой базы:
$$ 45 — 0 = 45 $$
Шаг 3
Расчет суммы оснований
$$ 9 + 45 = 54 $$
Шаг 4
Разделите сумму на 2
$$ \ frac {54} {2} = \ boxed {27} $$
Задача 8
Какова длина среднего сегмента SV трапеции ниже?
Показать ответ Шаг 1 Расчет длины оснований.Верхняя база:
$$ 17–8 = 9 $$
Шаг 2
Расчет низкой базы:
$$ 20 — 0 = 20 $$
Шаг 3
Расчет суммы оснований
$$ 9 + 20 = 29 $$
Шаг 4
Разделите сумму на 2
$$ \ frac {29} {2} = \ boxed {14.5} $$
Задача 9
Красный сегмент ниже среднего сегмента?
Показать ответ
Это не настоящий средний сегмент, потому что его длина не равна половине суммы длин оснований.
.