Структурная форма: 28. Структурная и приведенная формы модели. Идентификация модели

28. Структурная и приведенная формы модели. Идентификация модели

Система совместных, одновременных уравнений (или структурная форма модели) обычно содержит эндогенные и экзогенные переменные.

Эндогенные переменные – это зависимые переменные, число которых равно числу уравнений в системе и которые обозначаются через . Экзогенные переменные – это предопределенные переменные, влияющие на эндогенные переменные, но не зависящие от них. Обозначаются через .

Классификация переменных на эндогенные и экзогенные зависит от теоретической концепции принятой модели. Экономические переменные могут выступать в одних моделях как эндогенные, а в других как экзогенные переменные. Внеэкономические переменные (например, климатические условия, социальное положение, пол, возрастная категория) входят в систему только как экзогенные переменные. В качестве экзогенных переменных могут рассматриваться значения эндогенных переменных за предшествующий период времени (Лаговые переменные).

Структурная форма модели позволяет увидеть влияние изменений любой экзогенной переменной на значения эндогенной переменной. Целесообразно в качестве экзогенных переменных выбирать такие переменные, которые могут быть объектом регулирования. Меняя их и управляя ими, можно заранее иметь целевые значения эндогенных переменных.

Структурная форма модели в правой части содержит при эндогенных переменных коэффициенты и экзогенных переменных – коэффициенты , которые называются Структурными коэффициентами модели. Все переменные в модели выражены в отклонениях от среднего уровня, т. е. под подразумевается , а под – соответственно . Поэтому свободный член в каждом уравнении системы (3.3) отсутствует.

Использование МНК для оценивания структурных коэффициентов модели дает, как принято считать в теории, смещенные и несостоятельные оценки. Поэтому обычно для определения структурных коэффициентов модели структурная форма модели преобразуется в Приведенную форму модели.

Приведенная форма модели представляет собой систему линейных функций эндогенных переменных от экзогенных:

(3.4)

Где – коэффициенты приведенной формы модели,

– остаточная величина для приведенной формы.

По своему виду приведенная форма модели ничем не отличается от системы независимых уравнений, параметры которой оцениваются традиционным МНК. Применяя МНК, можно оценить , а затем оценить значения эндогенных переменных через экзогенные.

Коэффициенты приведенной формы модели представляют собой нелинейные функции коэффициентов структурной формы модели. Рассмотрим это положение на примере простейшей структурной модели, выразив коэффициенты приведенной формы модели через коэффициенты структурной модели.

Для структурной модели вида

(3.5)

Приведенная форма модели имеет вид

(3.6)

Из первого уравнения (3.5) можно выразить следующим образом (ради упрощения опускаем случайную величину):

.

Подставляя во второе уравнение (3.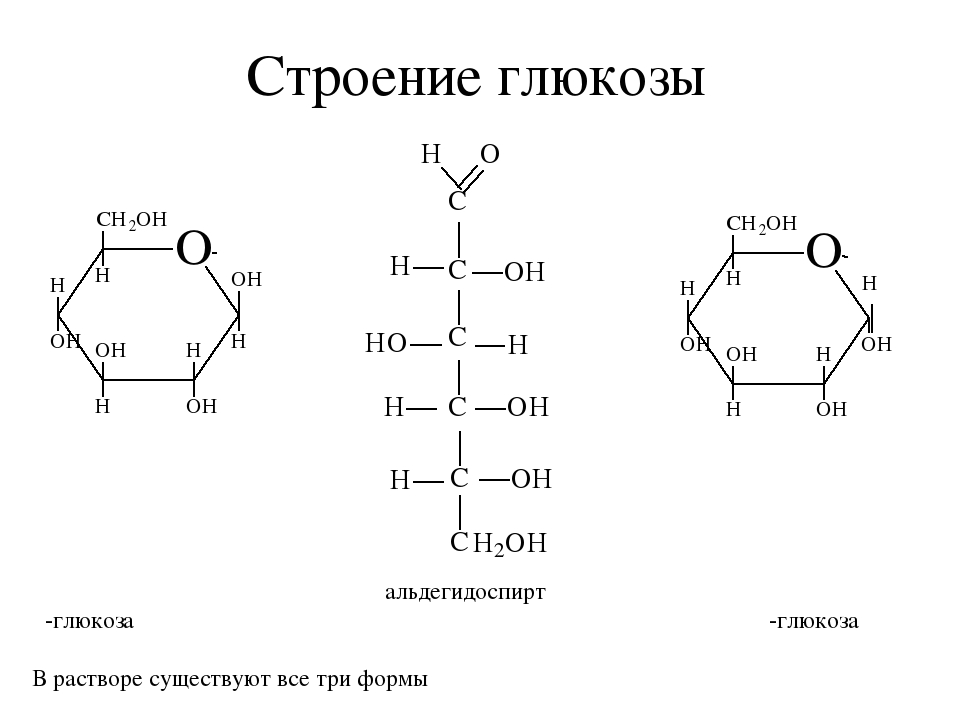 5), имеем

,

Откуда .

Поступая аналогично со вторым уравнением системы (3.5), получим

,

Т. е. система (8.5) принимает вид

Таким образом, можно сделать вывод о том, что коэффициенты приведенной формы модели будут выражаться через коэффициенты структурной формы следующим образом:

Следует заметить, что приведенная форма модели хотя и позволяет получить значения эндогенной переменной через значения экзогенных переменных, но аналитически она уступает структурной форме модели, так как в ней отсутствуют оценки взаимосвязи между эндогенными переменными.

При переходе от приведенной формы модели к структурной эконометрист сталкивается с проблемой идентификации. Идентификация – это единственность соответствия между приведенной и структурной формами модели.

Структурная модель (3.3) в полном виде содержит параметров, а приведенная форма модели в полном виде содержит параметров. Т. е. в полном виде структурная модель содержит большее число параметров, чем приведенная форма модели. Соответственно параметров структурной модели не могут быть однозначно определены из параметров приведенной формы модели.

Чтобы получить единственно возможное решение для структурной модели, необходимо предположить, что некоторые из структурных коэффициентов модели ввиду слабой взаимосвязи признаков с эндогенной переменной из левой части системы равны нулю. Тем самым уменьшится число структурных коэффициентов модели. Уменьшение числа структурных коэффициентов модели возможно и другим путем: например, путем приравнивания некоторых коэффициентов друг к другу, т. е. путем предположений, что их воздействие на формируемую эндогенную переменную одинаково. На структурные коэффициенты могут накладываться, например, ограничения вида .

С позиции идентифицируемости структурные модели можно подразделить на три вида:

1) идентифицируемые;

2) неидентифицируемые;

3) сверхидентифицируемые.

Модель Идентифицируема, если все структурные ее коэффициенты определяются однозначно, единственным образом по коэффициентам приведенной формы модели, т. е. если число параметров структурной модели равно числу параметров приведенной формы модели. В этом случае структурные коэффициенты модели оцениваются через параметры приведенной формы модели и модель идентифицируема.

Модель Неидентифицируема, если число приведенных коэффициентов меньше числа структурных коэффициентов, и в результате структурные коэффициенты не могут быть оценены через коэффициенты приведенной формы модели.

Модель Сверхидентифицируема, если число приведенных коэффициентов больше числа структурных коэффициентов. В этом случае на основе коэффициентов приведенной формы можно получить два или более значений одного структурного коэффициента. В этой модели число структурных коэффициентов меньше числа коэффициентов приведенной формы. Сверхидентифицируемая модель в отличие от неидентифицируемой модели практически решаема, но требует для этого специальных методов исчисления параметров.

Структурная модель всегда представляет собой систему совместных уравнений, каждое из которых требуется проверять на идентификацию.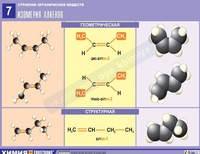 Модель считается идентифицируемой, если каждое уравнение системы идентифицируемо. Если хотя бы одно из уравнений системы неидентифицируемо, то и вся модель считается неидентифицируемой. Сверхидентифицируемая модель содержит хотя бы одно сверхидентифицируемое уравнение.

Выполнение условия идентифицируемости модели проверяется для каждого уравнения системы. Чтобы уравнение было идентифицируемо, необходимо, чтобы число предопределенных переменных, отсутствующих в данном уравнении, но присутствующих в системе, было равно числу эндогенных переменных в данном уравнении без одного.

Если обозначить число эндогенных переменных в -м уравнении системы через , а число экзогенных (предопределенных) переменных, которые содержатся в системе, но не входят в данное уравнение, — через , то условие идентифицируемости модели может быть записано в виде следующего счетного правила:

Таблица 3.1

	Уравнение идентифицируемо
	Уравнение неидентифицируемо
	Уравнение сверхидентифицируемо

Для оценки параметров структурной модели система должна быть идентифицируема или сверхидентифицируема.

Рассмотренное счетное правило отражает необходимое, но недостаточное условие идентификации. Более точно условия идентификации определяются, если накладывать ограничения на коэффициенты матриц параметров структурной модели. Уравнение идентифицируемо, если по отсутствующим в нем переменным (эндогенным и экзогенным) можно из коэффициентов при них в других уравнениях системы получить матрицу, определитель которой не равен нулю, а ранг матрицы не меньше, чем число эндогенных переменных в системе без одного.

Целесообразность проверки условия идентификации модели через определитель матрицы коэффициентов, отсутствующих в данном уравнении, но присутствующих в других, объясняется тем, что возможна ситуация, когда для каждого уравнения системы выполнено счетное правило, а определитель матрицы названных коэффициентов равен нулю. В этом случае соблюдается лишь необходимое, но недостаточное условие идентификации.

В эконометрических моделях часто наряду с уравнениями, параметры которых должны быть статистически оценены, используются балансовые тождества переменных, коэффициенты при которых равны . В этом случае, хотя само тождество и не требует проверки на идентификацию, ибо коэффициенты при переменных в тождестве известны, в проверке на идентификацию собственно структурных уравнений системы тождества участвуют.

< Предыдущая		Следующая >

53. Структурная форма модели: состав, виды переменных.

Исходная система (модель), которая отражает реальные связи между показателями, называется структурной формой модели (СФМ).

СФМ содержит

эндогенные и экзогенные переменные.

Переменные, которые являются только факторами во всех уравнениях модели, называются экзогенными (х₁,х₂).

Переменные, кот1орые хотя бы в одном из уравнений системы являются результатом, называются эндогенными (у₁,у₂).

Простейшая структурная форма модели имеет вид:

Классификация переменных на эндогенные и экзогенные зависит от теоретической концепции принятой модели.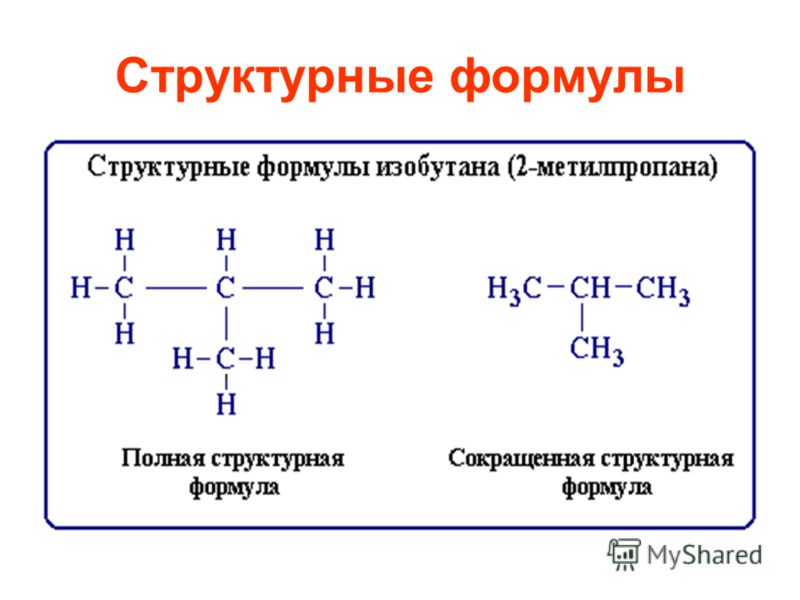 Экономические переменные могут выступать в одних моделях как эндогенные, а в других – как экзогенные. Внеэкономические переменные (например, климатические условия) входят в систему как экзогенные переменные.

В качестве экзогенных переменных могут рассматриваться значения эндогенных переменных за предшествующий период времени – это

лаговые переменные. Так, например, потребление текущего года (у_t) может зависеть не только от ряда экономических факторов, но и от уровня потребления в предыдущем году (у_t-1).

Структурная форма модели позволяет увидеть влияние изменений любой экзогенной переменной на значения эндогенной переменной. Структурная форма модели содержит в правой части при эндогенных и экзогенных переменных коэффициенты b_i(коэффициент при эндогенной) и a_j (при экзогенной), которые называются структурные коэффициенты модели. Все переменные в модели выражены в отклонениях от среднего уровня, т.е. под x подразумевается , а под у – соответственно . Поэтому свободный член в каждом уравнении отсутствует. Использование МНК для оценивания структурных коэффициентов модели дает, как принято считать в теории, смещенные и несостоятельные оценки. Поэтому обычно для определения структурных коэффициентов модели структурная форма модели преобразуется в приведенную форму модели.

Так как использоьвание МНК для оценивания структурных коэффициентов модели дает, как принято считать в теории, смещенные и несостоятельные оценки. Поэтому обычно для определения структурных коэффициентов модели структурная форма модели преобразуется в приведенную форму модели.

Приведенная форма модели представляет собой систему линейных функций эндогенных переменных от экзогенных:

Где — коэффициенты приведенной формы модели.

По виду приведенная форма ничем не отличается от системы независимых уравнений, параметры которой оцениваются традиционным способом МНК. Применяя МНК, можно оценить , а затем оценить значения эндогенных переменных через экзогенные.

Коэффициенты приведенной формы модели представляют собой нелинейные функции коэффициентов структурной формы модели. Коэффициенты приведенной функции выражаются из модели структурной.

Так, например, структурная модель имеет вид:

Приведенная форма модели имеет вид:

У₂ из первого уравнения структурной формы можно выразить как:

. Тогда система одновременных уравнений будет :

Отсюда имеем равенство:

=

=

— =

Таким образом, мы представили первое уравнение структурной формы модели в виде уравнения формы модели:

Т.е. мы выразили коэффициенты приведенной формы уравнения через соотношения коэффициентов структурной формы:

и

Аналогично доказываем связь коэффициентов приведенной формы модели второго уравнения с коэффициентами структурной модели:

и

Приведенная форма модели хотя и позволяет получить значения эндогенной переменной через значения экзогенных переменных, аналитически уступает структурной форме модели, так как в ней нет оценки взаимосвязи между эндогенными переменными.

14 Типы конструктивных форм для высотных зданий

Структурные формы, также известные как конструктивные системы, представляют собой механизм, обеспечивающий структурную устойчивость здания. Для одного и того же высотного здания можно использовать одну или несколько структурных систем в зависимости от характера конструкции. Решение о пригодности системы сопротивления поперечной нагрузке должно приниматься инженером-строителем, хорошо разбирающимся в расчете конструкции и проектировании высотных зданий.

Что такое высотное здание

Отсутствует специально указанная линия разграничения для разделения высотных и малоэтажных зданий. Однако, согласно методам, используемым в мире, здания выше 20 этажей могут считаться высотными зданиями.

Высотные здания должны быть спроектированы таким образом, чтобы выдерживать гравитационные нагрузки и боковые нагрузки из-за воздействия ветра , землетрясения и т. д. боковая устойчивость здания. В зависимости от высоты и других особенностей здания выбирается наиболее подходящая конструктивная система.

Требования учитываются при проектировании высотных зданий.

Боковое отклонение высотного здания

Как правило, боковое отклонение высотного здания ограничено до (высота/500) . Превышение этого предела может повлиять на требования таких служб, как лифты.

Кроме того, чрезмерный прогиб может привести к растрескиванию ненесущих элементов, таких как кирпичные стены, облицовка, стеклянные перегородки и т. д. Это может привести к распределению нагрузок из-за потери жесткости.

Кроме того, чрезмерное отклонение может ощущаться пассажиром как дискомфорт.

Индекс сноса

Пассажиры действительно почувствовали относительный прогиб между этажами. Индекс дрейфа — это индикатор, который показывает, находимся ли мы в пределах или нет.

Далее индекс дрейфа рассматривается как показатель поперечной жесткости здания.

Боковой снос здания обычно ограничивается ( 1/500 ).

Снос можно рассчитать по общему сносу или межэтажному сносу.

Общий снос = Максимальный боковой прогиб здания = Δ 1

Индекс общего сноса = Δ 1 / высота здания

Междуэтажный снос = Разница бокового прогиба двух плит (например: 21 этаж и 22 этаж) = Δ 2

Индекс сноса = Δ 2 / высота от пола до пола

Кроме того, ограничение вибраций пола и ускорений здания также является обязательным условием для поддержания человеческого комфорта. Здание должно быть достаточно жестким, чтобы ограничить его максимальное ускорение до минимального уровня, ощущаемого человеком.

Конструктивные формы для высотных зданий

Высотные здания становятся все более популярными в мире с развитием, и также стало модным строить высотные здания.

Из-за ограниченной площади земли в перегруженных районах наиболее удобным вариантом является строительство высокого здания для размещения всех служб. Высотные здания строятся в виде смешанной застройки, жилых домов, офисных помещений и т. д.

Как обсуждалось выше, при проектировании высотных зданий необходимо учитывать ключевые факторы. Кроме того, в зависимости от характера конструкции инженер-строитель должен выбрать подходящие конструктивные системы для продолжения проектирования.

Кроме того, эти структурные формы, обсуждаемые ниже, могут быть идентифицированы как системы сопротивления боковой нагрузке.

В этой статье мы обсуждаем 14 различных структурных форм.

1. Каркасные конструкции со связями
2. Каркасные конструкции с жестким каркасом
3. Каркасные конструкции с заполнением
4. Конструкции с жесткими стенками 9 0068
5. Соединённые конструкции стен жесткости
6. Каркасные конструкции стен
7. Каркасные трубчатые конструкции
8. Трубчатые конструкции или каркасно-корпусные конструкции
9. Трубчатые конструкции в виде пучков
10. Трубчатые конструкции со связями 9001 1
11. Конструкции с аутригером
12. Подвесные конструкции
13. Пространственные конструкции
14. Гибридные конструкции

Каркасные конструкции

Конструкции каркасного каркаса в основном сооружаются в стальных зданиях. Стальные здания имеют сравнительно слабую боковую устойчивость по сравнению с той же шкалой 9.0009 бетон строительный.

Они деформируются при приложении боковых нагрузок от ветра, землетрясения и т. д. без особого сопротивления из-за отсутствия поперечной жесткости. Таким образом, рамы раскрепляются и преобразуют конструкцию в растянутую рамную конструкцию, чтобы нести эти боковые нагрузки на фундамент.

Элементы, закрепленные между рамой, воспринимают боковые нагрузки в виде осевого растяжения или силы сжатия. Эти элементы проектируются после проведения анализа боковых нагрузок.

Существуют различные типы систем боковых распорок.

• Одинарные диагонали
• Крестовины
• К-образные связи
• V-образные связи 9 0068

Одинарные диагонали

Скобы крепятся по диагонали рамы. Когда эти рамы закреплены, они располагаются таким образом, что воспринимают осевые растягивающие усилия. Члены могут нести более высокие растягивающие усилия, чем силы сжатия. Следовательно, диагонали фиксируются в обоих направлениях, чтобы нести боковые силы, действующие в любом направлении.

Затем мы можем спроектировать опоры для растягивающих усилий. Кроме того, сбой при сжатии минимален.

Крепление со стороны приложения нагрузки воспринимает боковую нагрузку как силу растяжения.

Распорка поперечная

Раскосы, закрепленные по диагонали путем пересечения друг друга, выполнены. На следующем рисунке показано расположение поперечных распорок.

Крестовины крепятся к основным рамам по-разному. Вместо одной распорки, как показано на рисунке выше, распорки также могут быть закреплены между внутренними рамами.

К-образные распорки

На следующем рисунке показано расположение К-образных распорок.

Скобы крепятся на середине высоты колонны.

V-образные распорки

Распорки закреплены в форме буквы «V».

Добавление распорок к конструкции рамы уменьшает боковое отклонение.

Жесткая рамная конструкция

Каркасная конструкция обеспечивает устойчивость здания и является одной из наиболее широко используемых конструктивных форм. Балки и колонны соединены жесткими соединениями в качестве моментных соединений в этой конструктивной системе.

• Жесткие каркасные конструкции обеспечивают больше свободного пространства благодаря прямоугольным каркасным конструкциям на уровне пола. Дает больше свободы в планировке этажей.
• Проектирование и строительство жестких каркасных конструкций возможно до 20-25 этажей. За этими пределами было бы труднее контролировать боковой снос из-за боковой нагрузки, поскольку они становятся критическими с увеличением высоты.
• Однако в стальных зданиях нельзя построить 20-25 этажей без боковых связей. Поэтому такие конструкции больше подходят для железобетонных конструкций, где бетонные колонны и балки обладают достаточной жесткостью.

• Сетка колонн может быть увеличена примерно на 6-9м.
• Боковая устойчивость обеспечивается колонной, балкой и соединением балки с колонной
• Кроме того, на размеры колонн и балок сильно влияют боковые нагрузки в дополнение к гравитационным нагрузкам.
• С увеличением высоты здания размер элементов и расстояние между колоннами можно регулировать для достижения требуемой жесткости.
• Увеличение высоты здания увеличивает последующую нагрузку, которая будет действовать как сила сдвига на колонны. Размер колонны должен быть сделан на основе этих сил, приложенных к ним.
• Кроме того, изгибающие моменты из-за боковых нагрузок будут увеличиваться на более низких уровнях. Поэтому на нижних уровнях требуется более глубокий луч. Кроме того, не на всех этажах будет возможна одинаковая высота балки.

Каркасные конструкции с заполнением

Стены с заполнением из каменной кладки могут использоваться для повышения устойчивости здания к боковой нагрузке. Кирпичная стена, построенная внутри бетонного каркаса, образует такие конструкции.

Кроме того, вертикальное продолжение стен заполнения важно учитывать для обеспечения поперечной устойчивости. Не обязательно, чтобы все стены были залиты кирпичной кладкой. Однако хотя бы одна панель может быть заполнена.

Как правило, эти стены не учитывают поперечную устойчивость в зданиях средней этажности при проверке на сейсмические нагрузки.

Качество кирпича, используемого для этих стен, очень важно для создания прочной конструкции. Трещины в стене можно рассматривать как потерю жесткости стены. Наличие крупных трещин в стене не позволяет нам считать эту стену поперечной устойчивостью.

Одна из наиболее важных проблем заключается в том, что они со временем исчезают. Когда планы меняются или клиент меняется, им нужны разные внутренние-внешние договоренности. Таким образом, они удаляют заполняющие стены. Это значительно влияет на поперечную устойчивость конструкции, если она поддерживается заполненными стенами.

Таким образом, учет поперечной устойчивости рамы может быть более полезным и безопасным для таких конструктивных форм.

Стеновые конструкции, работающие на сдвиг

Бетонные стены, построенные вертикально закрепленными в основании с жесткостью для передачи вертикальных и горизонтальных нагрузок, приложенных к ним, могут быть идентифицированы как стены сдвига.

В зависимости от высоты и площади этажа здания необходимо построить достаточное количество стен жесткости с достаточной площадью поперечного сечения, чтобы обеспечить необходимую жесткость для выдерживания боковых нагрузок.

Стены жесткости изготавливаются в качестве подъемных стен, основных стен лестничных клеток, перегородок и т. д., где они могут быть продолжены от основания до крыши.

Поскольку бетонные стены более жесткие, чем жесткая бетонная балка и колонная конструкция, конструкции стен сдвига могут быть построены примерно до 34 этажей.

Следующее можно считать важным, относящимся к конструкциям, построенным со стенками жесткости.

• Использование стен жесткости в строительстве больше подходит для зданий с повторяющимися этажами. Как обсуждалось выше, нам нужно продолжить стены сдвига по вертикали. Следовательно, повторение добавляет множество преимуществ к конструкции конструкции, а также к стоимости строительства.
• Конструкции до 35 этажей могут быть рассчитаны на боковые нагрузки с учетом только стен жесткости. Взаимодействие жесткой стены и конструкции каркаса можно считать минимальным. В этом методе мы проектируем стены сдвига, чтобы нести все боковые нагрузки без передачи на раму.
• Кроме того, колонны могут быть рассчитаны на вертикальные нагрузки от конструкции и изгибающий момент от балок на основе различных вариантов нагрузки и альтернативных нагрузок .
• При планировке стен жесткости следует располагать таким образом, чтобы к ним прилагались достаточные вертикальные нагрузки. Боковые нагрузки на стены создают растягивающие напряжения, если они не уравновешиваются сжимающими напряжениями, возникающими из-за вертикальных нагрузок. Кроме того, если стена сжимается, у нас может быть экономичная конструкция.
• В высотных зданиях иногда производится уменьшение толщины и длины стен, демонтаж стен и т.д. Эти действия оказывают значительное влияние на поведение конструкции. Изменения такого рода должны выполняться с большой осторожностью и тщательным анализом конструкции.
• Когда стены жесткости не расположены симметрично ни в одном направлении, конструкция будет искривляться при приложении боковых нагрузок. Эти действия должны учитываться при проектировании, и программное обеспечение для компьютерного анализа должно использоваться для моделирования конструкции, чтобы найти поведение.

Сдвоенные конструкции стен жесткости

В большинстве высотных зданий стены жесткости сооружаются вокруг стен лифтов. Как правило, они выровнены в любом направлении. Далее, между ядрами лифта есть вестибюли.

Эти ядра лифта могут быть соединены бетонными балками, создавая взаимодействие между стеной в двух ядрах. Когда две стены сдвига, соединенные рамой сопротивления моменту, называют связанной стеной сдвига. Это соединение повышает устойчивость конструкции к боковой нагрузке, чем стены действуют отдельно.

На приведенном выше рисунке показано расположение сопряженной стены сдвига и то, как она выглядит при моделировании. Как обсуждалось выше, мы используем для соединения стенок сдвига, чтобы повысить их способность противостоять нагрузкам в дальнейшем. На следующем рисунке четко показан диапазон улучшений, которые могут быть достигнуты за счет соединения стенок сдвига.

Каркасные конструкции стен

Конструкции, в которых учитывается взаимодействие стены и каркасов, считаются каркасными стеновыми конструкциями. При этажности более 15-20 этажей можно учитывать взаимодействие стен и рам.

Кроме того, учет взаимодействия каркаса стены значительно улучшает поперечную устойчивость здания в этих типах структурных форм.

Стена сдвига вместе с консолью и рамой показывает деформацию сдвига при приложении боковых нагрузок. Комбинация этих двух действий уменьшает боковое отклонение здания.

Таким образом, как показано на рисунке выше, нижняя часть конструкций демонстрирует поведение на изгиб, а верхний сегмент демонстрирует поведение на сдвиг.

Следующие преимущества можно выделить как полезные при использовании стеновых каркасных конструкций.

• Боковая деформация/дрейф намного ниже, чем при рассмотрении стены сдвига вдоль.
• Значительное снижение момента обваловки стен/несущих стен на уровне подвала.
• Колонны могут быть выполнены раскосными.

Компьютерный анализ может быть выполнен для получения точного поведения элементов конструкции и их сил.

Каркасные трубчатые конструкции

Способность внутренних бетонных стен сопротивляться боковой нагрузке ограничивается увеличением высоты здания по сравнению с площадью здания.

Длина стен жесткости в направлении приложения боковых нагрузок является мерой поперечной жесткости в этом направлении. Но есть ограничения. Мы не можем продолжать сдвигать стены по всему полу.

В таких сценариях было бы полезно рассмотреть действие каркасной трубы из других конструктивных форм.

Конструкция внешней рамы может использоваться для сопротивления боковым нагрузкам. Чтобы выполнить это действие, необходимо увеличить глубину балок и высоту колонн.

Однако есть ограничения по увеличению размеров элементов на фасаде, так как мы должны уменьшить размер окон. Если мы можем создать раму вокруг здания, как показано на рисунке выше, можно выдержать более высокую нагрузку, поскольку она действует как трубчатая конструкция.

Колонны на расстоянии 2-4 м с глубокими балками по периметру образуют трубчатую конструкцию.

Как бетонные, так и стальные конструкции могут быть выполнены в виде трубчатых конструкций. Кроме того, этим методом можно проектировать и строить 40-60-этажные здания.

Несмотря на то, что прямоугольная форма более эффективна, могут быть изготовлены и другие формы, такие как круглая и восьмиугольная.

Трубчатые или корпусные конструкции

Эти типы конструктивных форм обладают хорошей устойчивостью к боковой нагрузке.

Основные стены, которые могут быть построены для облегчения подъема и лестниц, могут рассматриваться как внутренние трубы.

Эта система является еще одним шагом вперед по сравнению с трубчатой ​​конструкцией рамы, которую мы обсуждали ранее.

В этой конструкционной системе основные стены взаимодействуют с трубой по периметру, увеличивая несущую способность в поперечном направлении.

Сборные трубчатые конструкции

Эта форма конструкции используется в самых высоких конструкциях.

Эта система представляет собой комбинацию нескольких трубок.

Эта конструктивная система используется в самом высоком здании, для которого потребовались более жесткие ребра жесткости на нижних уровнях. Кроме того, эта система обладает очень высокой устойчивостью к боковой нагрузке.

Трубчатые конструкции с раскосами

Эти типы структурных форм могут быть изготовлены из стали или бетона.

Раскосная рама, закрепленная вокруг трубы, обеспечивает очень высокое сопротивление боковой нагрузке. Кроме того, крепление распорок такого типа не влияет на внутреннее устройство пола.

Однако это может повлиять на расположение фасада и окон.

Раскосы соединены со всеми колоннами, что обеспечивает более равномерное распределение боковых сил. Далее за счет соединения раскосов и вертикальных колонн осевые нагрузки на колонны будут распределяться друг на друга.

Колонны с большей осевой нагрузкой передают нагрузку на колонны с меньшей нагрузкой .

Раскосные конструкции с выносными опорами

Конструктивная эффективность высотных зданий сильно зависит от поперечной жесткости и сопротивления. Из доступных структурных систем чаще используются системы с выносными опорами, особенно в зданиях с повторяющимися этажами.

Глубокая балка или стена высотой от пола до пола или стальные фермы, построенные между двумя этажами, могут рассматриваться как выносные опоры. Он соединяет ядро ​​и периметр.

Назначение аутригера состоит в том, чтобы соединить внутренние конструкции и конструктивную систему по периметру, чтобы противостоять боковым нагрузкам. Следующие факторы могут повлиять на работу системы аутригеров как одной из полезных конструктивных форм.

• Локации построены по всей высоте здания. Если мы спроектируем правильно, метод проб и ошибок можно будет использовать для выбора наилучшего положения аутригера. Места, которые минимизируют боковые отклонения, могут быть выбраны моделью компьютерного анализа.
• Количество уровней аутригеров предусмотрено
• Их расположение в плане
• 9001 0 Наличие ленточных ферм для взаимодействия с соседними колоннами по периметру вместо стойки вместе с мегаколоннами
• Глубина фермы с выносными опорами

На следующем рисунке показаны сокращения, которые могут быть достигнуты за счет установки системы с выносными опорами в высотном здании. Соединение стенок сдвига сердечника усиливает изгибающий момент сердечника.

Вместо того, чтобы соединять периметр с ядром, что создает много проблем с функциями здания, можно построить по периметру ленточные фермы. Это позволяет пользователям эффективно использовать пол. Обычно полы с выносными опорами используются в качестве служебных полов.

Использование большего количества аутригеров снижает эффективность дополнительных аутригеров. Как правило, в здании может быть около 5 аутригеров. Кроме того, наличие двух аутригеров более эффективно, чем наличие одного.

Подвесные конструкции

Ключевым элементом этих типов конструкций является сердечник. Ядро может быть построено из бетонных стен или из элементов фермы.

Все перекрытия, выступающие из ядра, висят на элементах, начиная с уровня крыши. На уровне первого этажа будет достаточно места.

Кроме того, такие конструкции, как подвесные мосты и т. д., также могут рассматриваться как подвесные конструкции.

Космические конструкции

Трехмерная пространственная конструкция воспринимает вертикальные и горизонтальные нагрузки, приложенные к конструкции.

Основной системой сопротивления нагрузкам является трехмерная пространственная структурная система.

Структурный анализ и проектирование этих конструкций сравнительно очень сложны из-за сложного характера конструкции.

Модель компьютерного анализа может быть использована для понимания поведения конструкции, например путей нагрузки и т. д.

Гибридные конструкции

Гибридные конструкции представляют собой конструкции из нескольких комбинаций структурных систем, рассмотренных выше.

Из-за различных комбинаций гибридные структуры становятся более сложными структурными формами.

Кроме того, сочетание этих структур позволяет создавать очень специальные структурные системы. Кроме того, они могли бы быть более внимательными к форме.

Структурный анализ и проектирование усложняются из-за интеграции различных систем в рамках одной конструкции. Кроме того, эти комбинации должны выбираться и решаться на основе применимости характера конструкции.

Из-за сложности конструктивной системы требуется детальное исследование при анализе и проектировании этих конструкций. Кроме того, необходимо выполнить компьютерный анализ с использованием подходящего программного обеспечения, чтобы узнать общее поведение конструкции.

Формула, структурная | Encyclopedia.com

Полные структурные формулы

Сокращенные структурные формулы

Формулы линий

Трехмерные формулы

Ресурсы

Структурная формула — это химическая формула, которая дает более полное представление о соединении, чем его молекулярная формула. . В то время как молекулярная формула, такая как H ₂ O, показывает типы атомов в веществе и количество атомов каждого вида, структурная формула также дает информацию о том, как атомы связаны друг с другом. Некоторые сложные типы структурных формул могут даже дать вам представление о том, как атомы молекулы расположены в пространстве. Структурные формулы чаще всего используются для представления молекулярных, а не ионных соединений.

Существует несколько различных способов представления соединений в структурных формулах, в зависимости от того, насколько подробно необходимо показать рассматриваемую молекулу. Мы рассмотрим полные структурные формулы, сокращенные формулы, линейные формулы и трехмерные формулы.

Полные структурные формулы показывают все атомы в молекуле, типы связей между ними и то, как они связаны друг с другом. Для простой молекулы, такой как вода, H ₂ O, молекулярная формула, становится H—O—H, структурной формулой. Эта структурная формула показывает, что в молекуле воды атом кислорода является центральным атомом и соединен одинарными ковалентными связями с атомами водорода. Углекислый газ, СО ₂ , структурно можно представить как O=C=O. Эта структурная формула говорит вам о том, что в данном случае атом углерода является центральным, а атомы кислорода соединены двойными ковалентными связями с атомом углерода.

Для таких малых молекул количество новой информации в структурной формуле невелико, но структура становится более важной, когда мы изучаем более крупные молекулы. Давайте посмотрим на молекулярную формулу C ₂ H ₆ O. Имея некоторые знания о валентности трех типов задействованных атомов, мы можем расположить эти атомы в полной структурной формуле, как показано ниже.

Это формула этанола, известного своими опьяняющими и антисептическими свойствами, который также используется в реформулированном бензине. Это жидкость с температурой кипения 172°F (78°C). Однако мы также можем получить другую структурную формулу, которая удовлетворяет всем требованиям к связыванию вовлеченных атомов, но показывает совершенно другую молекулу.

Эта молекула представляет собой метиловый эфир. Это газ при комнатной температуре, химические свойства которого сильно отличаются от этанола.

КЛЮЧЕВЫЕ ТЕРМИНЫ

Химическая формула — Способ показать количество и тип атомов, объединенных вместе в одном чистом веществе.

Соединение — Чистое вещество, состоящее из двух или более элементов в определенных пропорциях, соединенных химическими связями. Свойства соединения могут сильно отличаться от свойств элементов, из которых оно сделано.

Ковалентное соединение — Химическое соединение, в котором общие электроны используются для образования связей между атомами. Атомы не становятся электрически заряженными, как в ионных соединениях.

Ионное соединение — Соединение, состоящее из положительных ионов (обычно ионов металлов) и отрицательных ионов (ионов неметаллов), удерживаемых вместе за счет электростатического притяжения.

Молекула — Химическое соединение, скрепленное ковалентными связями.

Валентность — Объединяющая способность атома или количество связей, которые он может образовать с другими атомами. В примерах, используемых в этой статье, атомы углерода могут образовывать четыре связи, атомы кислорода могут образовывать две связи, а атомы водорода могут образовывать одну связь.

После того, как вы ознакомитесь с правилами написания полных структурных формул, вы обнаружите, что используете сокращения и сокращенные структурные формулы. Вам все еще нужно показать всю молекулу, но неактивные части можно показать более схематично. Таким образом, приведенные выше две формулы в сокращенном виде выглядят следующим образом:

CH 3 CH 2 OH этиловый спирт

CH 3 OCH 9047 7 3 диметиловый эфир

Даже сокращенные формулы занимают много места и много времени для написания. Их можно еще больше преобразовать с помощью сокращенных формул линий, которые показывают основные связи молекулы вместо отдельных атомов и показывают конкретный атом только в том случае, если он отличается от углерода или водорода или если он участвует в реакции. на рассмотрении. Наши примеры сокращенных формул выглядят так, когда они представлены линейными формулами.

В каждой непомеченной вершине линий есть атом углерода с достаточным количеством атомов водорода, чтобы удовлетворить его валентность, равную четырем. Существует также атом углерода с сопровождающими его атомами водорода на конце любой линии связи, на которой не видно какого-либо другого атома. Сравните сокращенные формулы этих трех соединений с сокращенными формулами, чтобы найти атомы, подразумеваемые в формулах линий.

Все эти структурные формулы показывают вам плоскую молекулу на плоском листе бумаги. Однако большинство углеродсодержащих молекул трехмерны; некоторые из атомов прилипают к вам от углеродной цепи, а некоторые выступают за молекулу. Химики разработали специальные способы показать эти проецирующиеся вперед и назад атомы, чтобы понять, как ведут себя трехмерные молекулы. Эти трехмерные структурные формулы часто используются при изучении сложных молекул.