Трапеция фигура: Трапеция — геометрия и искусство

Трапеция. Свойства и элементы трапеции

Виды трапеций

Равнобедренная трапеция — это вид трапеции с равными боковыми сторонами.

Также встречаются такие названия, как равнобокая или равнобочная.

Прямоугольная трапеция — это трапеция, у которой углы при боковой стороне прямые.

Элементы трапеции

a, b — основания трапеции (a параллельно b),

m, n — боковые стороны трапеции,

d₁, d₂ — диагонали трапеции,

h — высота трапеции (отрезок, соединяющий основания и при этом перпендикулярен им),

MN — средняя линия (отрезок, соединяющий середины боковых сторон).

Площадь трапеции

1. Через полусумму оснований a, b и высоту h: S = \frac{a + b}{2}\cdot h
2. Через среднюю линию MN и высоту h: S = MN\cdot h
3. Через диагонали d₁, d₂ и угол (\sin \varphi) между ними: S = \frac{d_{1} d_{2} \sin \varphi}{2}

Свойства трапеции

Средняя линия трапеции

Средняя линия параллельна основаниям, равна их полусумме и разделяет каждый отрезок с концами, находящимися на прямых, которые содержат основания, (к примеру, высоту фигуры) пополам:

MN || a, MN || b, MN = \frac{a + b}{2}

Сумма углов трапеции

Сумма углов трапеции, прилежащих к каждой боковой стороне, равна 180^{\circ}:

\alpha + \beta = 180^{\circ}

\gamma + \delta =180^{\circ}

Равновеликие треугольники трапеции

Равновеликими, то есть имеющими равные площади, являются отрезки диагоналей и треугольники AOB и DOC, образованные боковыми сторонами. {2}.

Отношение длин отрезков и оснований

Каждый отрезок, соединяющий основания и проходящий через точку пересечения диагоналей трапеции, поделен этой точкой в отношении:

\frac{OX}{OY} = \frac{BC}{AD}

Это будет являться справедливым и для высоты с самими диагоналями.

Описанная около трапеции окружность

Каждая равнобокая трапеция может содержать описанную окружность. Только равнобокую трапецию возможно вписать в окружность.

Вписанная в трапецию окружность

Треугольники AOB и DOC являются прямоугольными, если трапеция ABCD описана около окружности. Центром же вписанной окружности будет являться точка O.

Опущенные на гипотенузы, высоты этих треугольников, тождественны радиусу вписанной окружности, а высота трапеции тождественна диаметру вписанной окружности.

Что такое трапеция: определение, виды, свойства

В данной публикации мы рассмотрим определение, виды и свойства (касательно диагоналей, углов, средней линии, точки пересечения боковых сторон и т. д.) одной из основных геометрических фигур – трапеции.

• Определение трапеции
• Виды трапеций
  • Равнобедренная трапеция
  • Прямоугольная трапеция
  • Разносторонняя трапеция
• Свойства трапеции
  • Свойство 1
  • Свойство 2
  • Свойство 3
  • Свойство 4
  • Свойство 5
  • Свойство 6
  • Свойство 7
  • Свойство 8

Определение трапеции

Трапеция – это четырехугольник, две стороны которого параллельны, а остальные две – нет.

Параллельные стороны называются основаниями трапеции (AD и BC), две другие стороны – боковыми (AB и CD).

Угол при основании трапеции – внутренний угол трапеции, образованный ее основанием и боковой стороной, например, α и β.

Трапеция записывается путем перечисления его вершин, чаще всего, это ABCD. А основаниям обозначаются маленькими латинскими буквами, например, a и b.

Средняя линия трапеции (MN) – отрезок, соединяющий середины ее боковых сторон.

Высота трапеции (h или BK) – это перпендикуляр, проведенный от одного основания к другому.

Виды трапеций

Равнобедренная трапеция

Трапеция, боковые стороны которой равны, называется равнобедренной (или равнобокой).

AB = CD

Прямоугольная трапеция

Трапеция, у которой оба угла при одной из ее боковых сторон прямые, называется прямоугольной.

∠BAD = ∠ABC = 90°

Разносторонняя трапеция

Трапеция является разносторонней, если ее боковые стороны не равны, и ни один из углов при основании не является прямым.

Свойства трапеции

Перечисленные ниже свойства применимы к любым видам трапеций. Свойства равнобедренной и прямоугольной трапеций представлены на нашем сайте в отдельных публикациях.

Свойство 1

Сумма углов трапеции, прилежащих к одной и той же боковой стороне, равна 180°.

α + β = 180°

Свойство 2

Средняя линия трапеции параллельна ее основаниям и равняется половине их суммы.

Свойство 3

Отрезок, который соединяет середины диагоналей трапеции, лежит на ее средней линии и равняется половине разности оснований.

• KL – отрезок, соединяющий середины диагоналей AC и BD
• KL лежит на средней линии трапеции MN

Свойство 4

Точки пересечения диагоналей трапеции, продолжений ее боковых сторон и середин оснований лежат на одной прямой.

• DK – продолжение боковой стороны CD
• AK – продолжение боковой стороны AB
• E – середина основания BC, т.е. BE = EC
• F – середина основания AD, т.е. AF = FD

Если сумма углов при одном основании равняется 90° (т. е. ∠DAB + ∠ADC = 90°), значит продолжения боковых сторон трапеции пересекаются под прямым углом, а отрезок, который соединяет середины оснований (ML) равняется половине их разности.

Свойство 5

Диагонали трапеции делят ее на 4 треугольника, два из которых (при основаниях) подобны, а два других (при боковых сторонах) равны по площади.

• ΔAED ~ ΔBEC
• S_ΔABE = S_ΔCED

Свойство 6

Отрезок, проходящий через точку пересечения диагоналей трапеции параллельно ее основаниям, можно выразить через длины оснований:

Свойство 7

Биссектрисы углов трапеции при одинаковой боковой стороне взаимно перпендикулярны.

• AP – биссектриса ∠BAD
• BR – биссектриса ∠ABC
• AP перпендикулярна BR

Свойство 8

В трапецию можно вписать окружность только в том случае, если сумма длин ее оснований равна сумме длин ее боковых сторон.

Т.е. AD + BC = AB + CD

Радиус вписанной в трапецию окружности равен половине ее высоты: R = h/2.

Форма, свойства, формула, определение, примеры

Трапеция завораживает, потому что она определяется на основе географии, к которой вы принадлежите. Если вы посещаете Великобританию по обмену и просите студента нарисовать для вас трапецию, то он нарисует ее как трапецию. Трапецию также называют трапецией в некоторых частях мира, и это тип четырехугольника с одной парой противоположных сторон, параллельных друг другу.

1.	Что такое трапеция?
2.	Свойства трапеции
3.	Типы трапеций
4.	Формула трапеции
5.	Часто задаваемые вопросы о трапеции

Что такое трапеция?

Трапеция, также известная как трапеция, представляет собой многоугольник с четырьмя сторонами или четырехугольник.

Он имеет один набор противоположных сторон, которые параллельны, и набор непараллельных сторон. Параллельные стороны известны как основания, а непараллельные стороны известны как катеты трапеции.

Определение трапеции

Трапеция — это четырехсторонняя замкнутая двумерная фигура, имеющая площадь и периметр. Две стороны фигуры параллельны друг другу и называются основаниями трапеции. Непараллельные стороны известны как стороны или боковые стороны трапеции. Кратчайшее расстояние между двумя параллельными сторонами называется высотой. Поскольку противоположные стороны параллельны друг другу, вычислить площадь трапеции несложно.

Свойства трапеции

Эти свойства трапеции отличают ее от других четырехугольников:

• Основания (верхнее и нижнее) параллельны друг другу
• Противоположные стороны равнобедренной трапеции имеют одинаковую длину
• Углы рядом друг с другом в сумме дают 180°
• Медиана параллельна обоим основаниям
• Длина медианы является средним значением обоих оснований, т.
  е. (a +b)/2
• Если обе пары противоположных сторон трапеции параллельны, она считается параллелограммом
• Если обе пары противоположных сторон параллельны, все стороны имеют одинаковую длину и расположены под прямым углом друг к другу, то трапецию можно рассматривать как квадрат
• Если обе пары противоположных сторон параллельны, ее противоположные стороны имеют одинаковую длину и расположены под прямым углом друг к другу, то трапецию можно рассматривать как прямоугольник

Типы трапеций

Существует три типа трапеций, они приведены ниже:

1. Равнобедренная трапеция
2. Лестничная трапеция
3. Правая трапеция

Равнобедренная трапеция

Если катеты или непараллельные стороны трапеции равны по длине, то она называется равнобедренной трапецией. Углы параллельных сторон (основания) в равнобедренной трапеции равны между собой. У равнобедренной трапеции есть линия симметрии и обе диагонали равны по длине.

В приведенной ниже равнобедренной трапеции XYZW, XY и WZ называются основаниями трапеции. WX и YZ называются катетами трапеции, так как они не параллельны друг другу.

Разносторонняя трапеция

Если ни стороны, ни углы трапеции не равны, то это разносторонняя трапеция. В приведенной ниже разносторонней трапеции все четыре стороны, то есть AB, BC, CD и DA, имеют разную длину. Основания, то есть DC и AB, параллельны друг другу, но имеют разную длину.

Прямоугольная трапеция

Прямоугольная трапеция, также называемая прямоугольной, имеет пару прямых углов. Эти виды трапеций используются для оценки площадей под кривой. В приведенной ниже прямой трапеции или прямоугольной трапеции есть два прямых угла, один в D, а другой в A. Одна пара противоположных сторон, то есть DC и AB, параллельны друг другу.

Формула трапеции

Есть две основные формулы трапеции, это:

• Площадь трапеции
• Периметр трапеции

Площадь трапеции

Площадь трапеции рассчитывается путем измерения среднего значения параллельных сторон и умножения его на высоту. Чтобы найти площадь трапеции, нужно знать длины двух ее параллельных сторон и расстояние (высоту) между ними. Это количество единичных квадратов, которое может поместиться внутри фигуры, и измеряется в квадратных единицах, таких как см ² , m ² , in ² и т. д. Формула площади (A) трапеции вычисляется по основаниям, т.е. a и b, высота которых равна h, которая является перпендикулярным расстоянием между a и b .

Отсюда площадь трапеции вычисляется по следующей формуле:

Площадь = [(AB + CD)/2] × h

A = [(a + b)/2] × h

Где,

• AB и CD = параллельные стороны
• а = более короткое основание
• b = удлиненная база
• ч = высота или высота над уровнем моря

Периметр трапеции

Периметр трапеции определяется как общая длина границы формы, т. е. сумма всех ее сторон. Так как трапеция является двумерной фигурой, то и периметр будет лежать только в двумерной плоскости.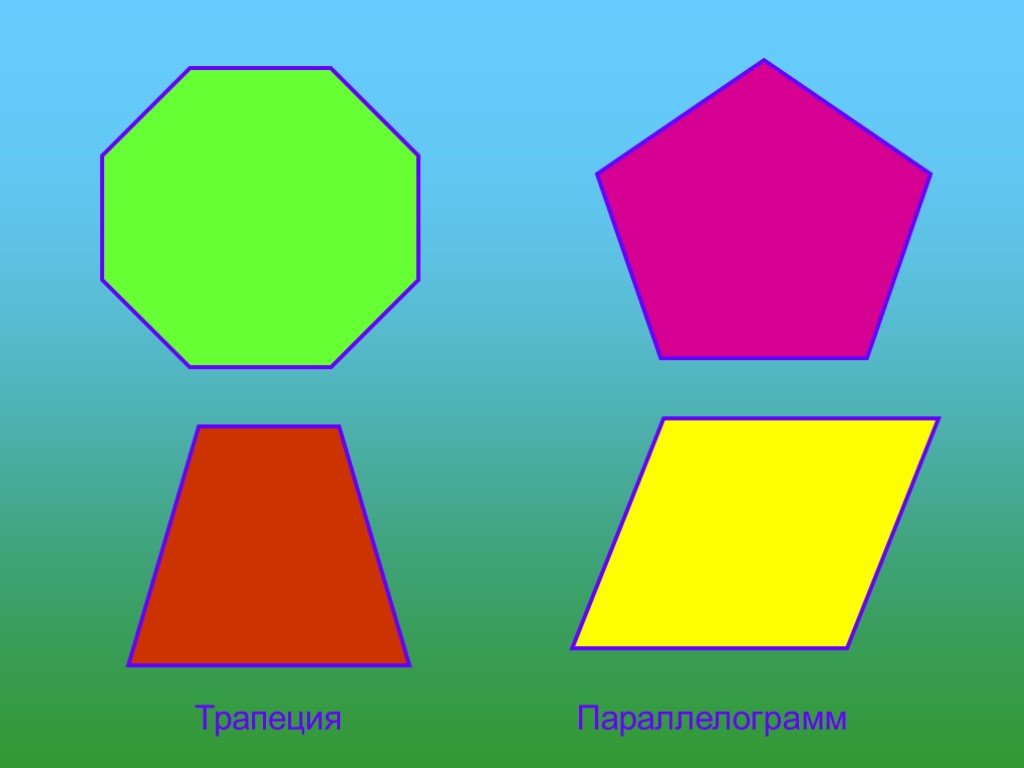 Рассмотрим трапецию ABCD, как показано ниже, с размерами сторон a, b, c и d. Давайте рассмотрим формулу трапеции. Формула периметра трапеции вычисляется путем нахождения суммы всех сторон, т. Е. AB + BC + CD + DA

Периметр трапеции = сумма всех сторон = a + b + c + d

, где a, b, c и d — стороны трапеции.

☛Связанные темы о трапеции

Ниже перечислены некоторые темы, связанные с трапецией.

• Рабочие листы трапеции
• Калькулятор периметра трапеции
• Ромб
• Площадь
• 3D-формы

 

Примеры трапеций

1. Пример 1: Если площадь трапеции 128 дюймов, а длины оснований 12 дюймов и 20 дюймов, какова будет высота трапеции?

   Решение:

   Предположим, что основания равны a и b, а высота трапеции равна h. Используя данную информацию,

   Мы должны найти h, который является расстоянием или высотой между основаниями. Подставим все эти значения в площадь трапеции по формуле:

   A = [(a + b)/2] × h

   128 = [(20 + 12)/2] × h

   256 = 32 × h

   h = 8 дюймов

   Следовательно, высота трапеция равна 8 дм.

2. Пример 2: Сару попросили найти площадь трапеции со сторонами 13, 8, 17 и 8 единиц. Вы можете помочь ей?

   Решение:

   Предположим, что a и b — основания, а h — высота данной трапеции.

   Вышеприведенная трапеция может быть представлена ​​следующим образом:

   13 + х + х = 17

   13 + 2х = 17

   2х = 4

   Следовательно, х = 2

   . из треугольников,

   8 ² = 2 ² + H ²

   64 = 4 + H ²

   H ² = 60

   H =

   9000 2
   9000 2
   9000 2 9000 2 ² = 60

   H =

   9 9000 2 ² = 60 9000 2

   H = ² = 60

   9000 2 ² .

   ×15

   h=2√15

   Наконец, мы воспользуемся формулой площади трапеции, чтобы найти ее площадь:

   A = [(a + b)/2] × h

   A = [(13 + 17)/2] × 2√15

   A = (60√15)/2

   A=30√15 квадратных единиц

   Следовательно, площадь данной трапеции равна 30√15 квадратных единиц

3. Пример 3: Четыре стороны трапеции имеют размеры 10 единиц, 7 единиц, 5 единиц и 9 единиц. Чему равен периметр трапеции?

   Решение: Периметр трапеции равен сумме всех сторон.

   Периметр = 10 + 7 + 5 + 9

   = 31 единица

   Следовательно, периметр данной трапеции равен 31 единице.

перейти к слайду перейти к слайду перейти к слайду

Отличное обучение в старшей школе с использованием простых подсказок

Увлекаясь зубрежкой, вы, скорее всего, забудете понятия. С Cuemath вы будете учиться визуально и будете удивлены результатами.

Запись на бесплатный пробный урок

Практические вопросы по трапеции

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о трапеции

Что такое трапеция?

Трапеция — это четырехсторонняя замкнутая 2D-форма, имеющая площадь и периметр. Его также называют трапецией. Стороны трапеции параллельны друг другу и называются основаниями трапеции. Непараллельные стороны известны как стороны или боковые стороны трапеции. Кратчайшее расстояние между двумя параллельными сторонами называется высотой.

Какие бывают трапеции?

Трапеции классифицируются на основе характера их сторон. Основные типы трапеций перечислены ниже:

• Равнобедренная трапеция
• Лестничная трапеция
• Правая трапеция

Каковы основные свойства трапеции?

Существует много свойств трапеции, некоторые из них перечислены ниже:

• Верхнее и нижнее основания трапеции параллельны.
• Равнобедренная трапеция состоит из равных по длине противоположных сторон.
• Углы рядом друг с другом в сумме дают 180°.

Как найти площадь трапеции?

Площадь трапеции вычисляется путем вычисления среднего значения двух параллельных сторон и умножения его на высоту.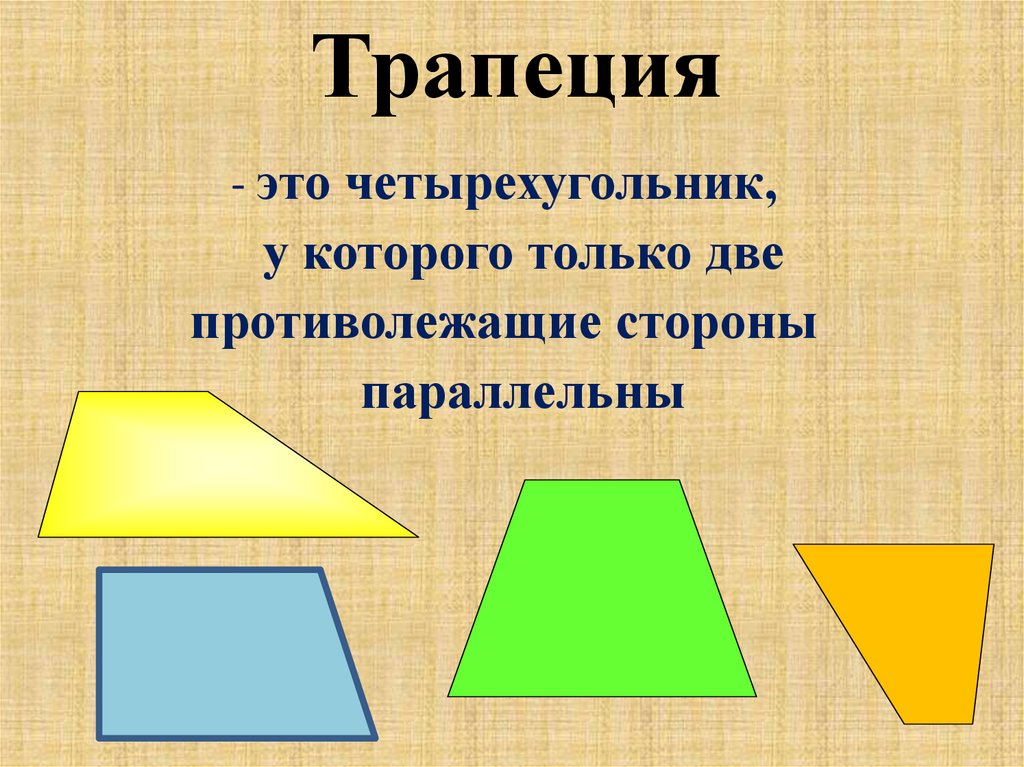

Площадь = [(a + b)/2] × h, где a и b — длины оснований, а h — высота.

Какое уравнение трапеции?

Есть два уравнения трапеции. Одно уравнение вычисляет его площадь; другой — его периметр. Периметр трапеции PQRS определяется как Периметр = PQ + QR + RS + PS. Площадь трапеции = [(a + b)/2] x h, где a и b — длины оснований, а h — высота.

Является ли трапеция четырехугольником?

Поскольку у трапеции четыре стороны, она автоматически становится четырехугольником. У него есть две стороны, которые параллельны, и две стороны, которые не параллельны.

Каковы три атрибута трапеции?

Тремя основными атрибутами трапеции являются следующие

1. Углы при основании и диагонали равны, если трапеция равнобедренная
2. Точка пересечения диагоналей лежит на одной прямой с серединами двух противоположных сторон
3. Противоположные стороны равнобедренной трапеции конгруэнтны

Как найти недостающую сторону трапеции?

Недостающую сторону трапеции можно определить по предоставленной вам информации. Если у вас есть площадь и длина основания, вы можете найти длину высоты. Вы также можете определить длину недостающей стороны, если знаете периметр и длину трех других сторон трапеции.

Диагонали трапеции равны?

Трапеции бывают трех видов — равнобедренные, разносторонние и прямые. В случае равнобедренной трапеции диагонали равны, так как непараллельные или катеты трапеции равны по длине. В случае разносторонней и прямой трапеции диагонали не равны.

Как рассчитать высоту трапеции по формуле трапеции?

Формула площади трапеции, A = [(a + b)/2] × h
Чтобы рассчитать высоту трапеции, мы можем вычислить площадь трапеции по формуле
. h = 2А/(а+b). Где «a» — более короткое основание, «b» — более длинное основание, «h» — расстояние между двумя основаниями, а A — площадь трапеции.

Каковы две основные формулы трапеций?

Две основные формулы трапеций:
Периметр трапеции равен сумме всех сторон. Выражается как P = a + b + c + d.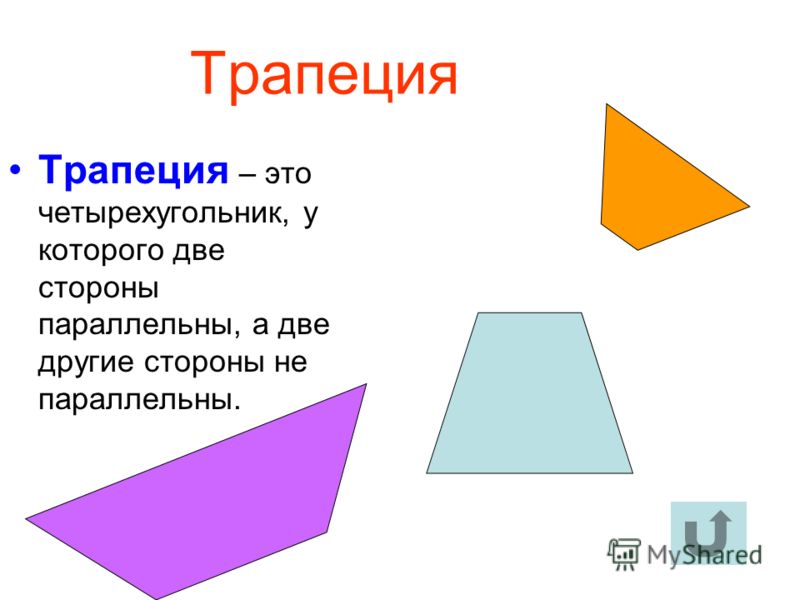 Где a, b, c и d — стороны трапеции.
Формула площади трапеции, A = [(a + b)/2] × h.

Свойства трапеций и изоберных трапеций

BY: Марк Райан и

Обновлен: 07-09-2021

От книги: GEOMETRY FOR DUMMEE

. 904. 904. 904. 904. 904. 904. 904. 9043 9043 904. 904. 9043 9043 9043

. 904. 9043 9043 9043 9043 9043 9043 9043 9043 9043 9043 . На Амазонке

Трапеция – это четырехугольник (форма с четырьмя сторонами) с ровно одной парой параллельных сторон (параллельные стороны называются

основаниями ). На следующем рисунке показана трапеция слева и равнобедренная трапеция справа.

• Свойства трапеции следующие:

• Свойства равнобедренной трапеции следующие:

  • Свойства трапеции применяются по определению (параллельные основания).

  • Ноги конгруэнтны по определению.

  • Нижние углы при основании равны.

  • Верхние углы при основании равны.

  • Любой нижний угол основания является дополнительным к любому верхнему углу основания.

  • Диагонали равны.

Дополнительные углы, пожалуй, труднее всего заметить на приведенных выше диаграммах. Из-за того, что стороны параллельны, последовательные углы являются односторонними внутренними углами и, таким образом, являются дополнительными. (Кстати, все специальные четырехугольники, кроме воздушного змея, содержат последовательные дополнительные углы.)

Вот вам доказательство равнобедренной трапеции:

Утверждение 1 :

Причина выписки 1 : Дано.

Утверждение 2 :

Причина утверждения 2 : Ножки равнобедренной трапеции конгруэнтны.

Утверждение 3 :

Причина утверждения 3 : Верхние углы при основании равнобедренной трапеции равны.

Заявление 4 :

Причина заявления 4 : Рефлексивное свойство.

Заявление 5 :

Разум для заявления 5 : СОЗДАТЕЛЬСТВО, ОЛИ SAS (2, 3, 4)

Заявление 6 :

. 6 : CPCTC (соответствующие части конгруэнтных треугольников конгруэнтны).

Заявление 7 :

Причина утверждения 7 : Если углы равны, то равны и стороны.

Эта статья из книги:

• Геометрия для чайников,

Об авторе книги:

Марк Райан — основатель и владелец Математического центра в районе Чикаго, где он занимается репетиторством по всем математическим предметам а также подготовка к тесту. Марк является автором исчисления для чайников, учебника исчисления для чайников 9.